Mean and median of a frequency distribution are 24 and 26.5 respectively. Find the mode using empirical formula. Solution in Bengali
Step by step video & image solution for Mean and median of a frequency distribution are 24 and 26.5 respectively. Find the mode using empirical formula. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A={a,b,c}and B={1,2,3,4} .Find the total number of relation from A to B.
01:38View SolutionDefine Pilot survey.
01:53View SolutionIf mode and mean of data are found 28 and 24 respectively, find median using empirical formula.
02:04View SolutionFor a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation
02:00View SolutionThe median and mode of a frequency distribution are 26 and 29 respectively. Then , the mean is
01:56View SolutionIf the mean and mode of a frequency distribution be 53.4 and 55.2 respectively, find the median
01:05View SolutionIf the mode and median of a frequency distribution are 31 and 37 respectively, find the arithmetic mean.
View SolutionIf the mean and median of a frequency distribution are 35 and 33 respectively, find mode.
05:37View SolutionThe mode of the following distribution table is 15. Find the mean of this data, and then find the median value by using empirical formula relating mean, median and mode.
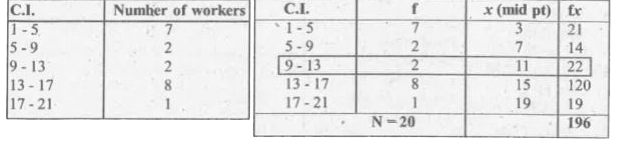 03:18View Solution
03:18View SolutionFind mode of the following frequency distribution.

The mean of above distribution is 53. Empirical formula to find approximate value of median.01:17View SolutionFind the mode and median of the data: By using the empirical relation also find the mean.
02:37View SolutionIf in the frequency distribution,the mean and median are 21 and 22 respectively,then find its mode.
00:57View SolutionIn a frequancy distribution,if the mean = 35 & median = 33, then find the mode of the frequency distribution.
01:14View SolutionIf the median and mean of moderately asymmetrical frequency distribution are 72 and 74 respectively, then the mode is
01:07View SolutionIf the mean and the mode of a moderately skewed frequency distribution are 90 and 96 respectively, then the median is
01:30View Solution

