A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?

1.2×108m/s
1.8×108m/s
2.4×108m/s
3.0×108m/s
The correct Answer is:B

1μ=sinθC=35⇒μ=53
⇒v=cμ=3×1085/3=95×108=1.8×108ms−1
Similar Questions
A metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA container of width 2a is filled with a liquid. A thin wire of weight per unit length λ is gently placed over the liquid surface in the middle of the surface as shown in the figure. As a result, the liquid surface is depressed by a distance y(y<<a). If the surface tension of the liquid is 4λagky. Then value of k is .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
AM gBMg−Vρ gCMg+ΠR2hgρDρg(V+ΠR2h)
Consider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index μ. A student finds that, irrespective of what the incident angle I (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is :
 View Solution
View SolutionA disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionA rectangular tank filled with some liquid is accelerated along a horizontal surface at 403ms−2. Inside the liquid, a laser pointer is fixed a the centre of the tank which shoots a thin laser beam in the vertically upward direction. If after refraction from the liquid surface, the laser beam moves along the surface of the liquid, then what is the refrctive index of the liquid ?
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
 View Solution
View SolutionA coin lies on the bottom of a lake 2m deep at a horizontal distance x from the spotlight (a source of thin parallel been of light) situated 1m above the surface of a liquid of refractive index μ=√2) and height 2m. Find x.
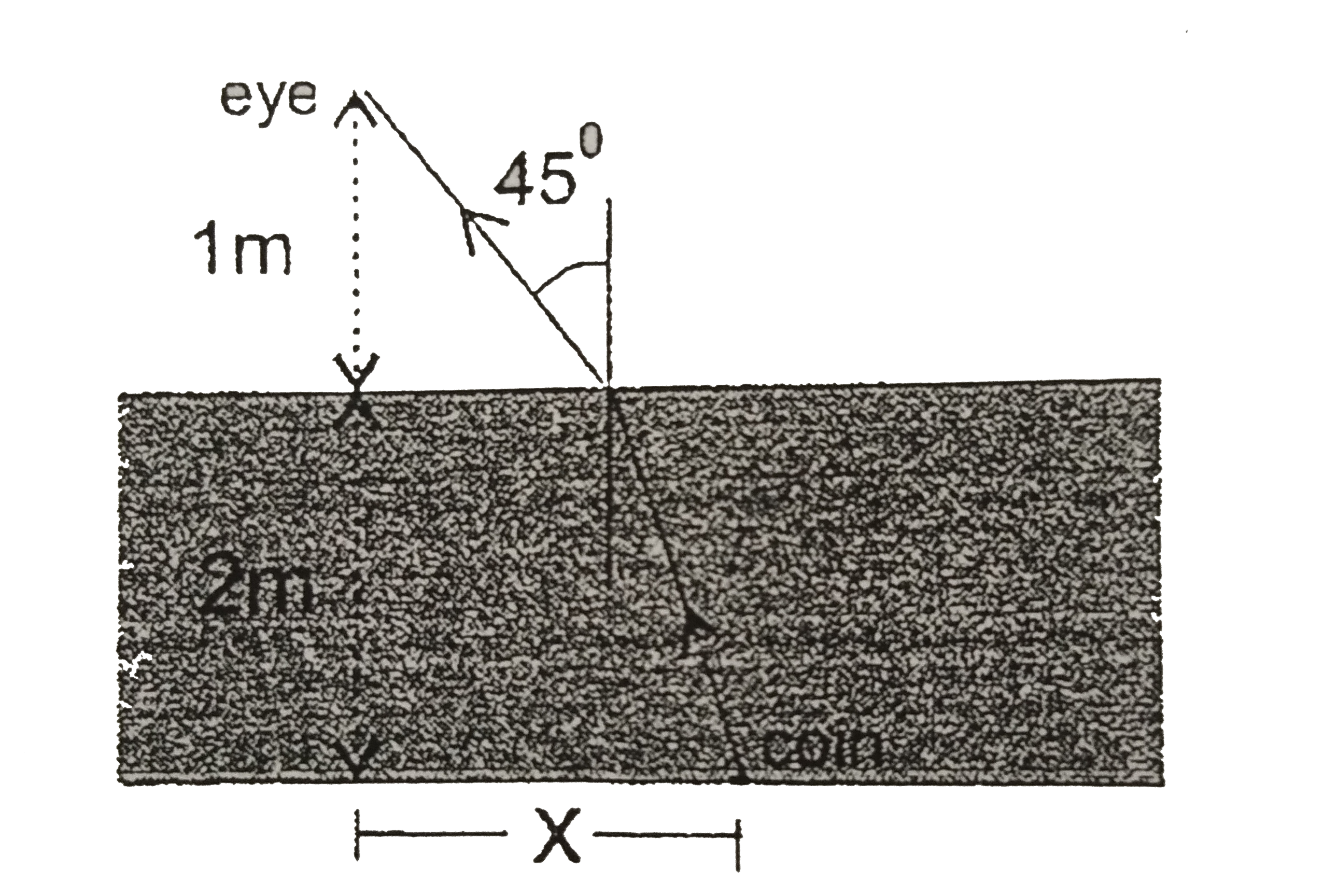 View Solution
View SolutionA small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
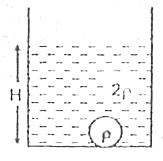 View Solution
View Solution

