A rectangular tank filled with some liquid is accelerated along a horizontal surface at . Inside the liquid, a laser pointer is fixed a the centre of the tank which shoots a thin laser beam in the vertically upward direction. If after refraction from the liquid surface, the laser beam moves along the surface of the liquid, then what is the refrctive index of the liquid ?
The correct Answer is:1.25
To solve the problem, we need to determine the refractive index of the liquid in the tank based on the given conditions. Here’s the step-by-step solution:
Step 1: Understand the Situation
The tank is accelerating horizontally with an acceleration a=403m/s2. A laser pointer shoots a beam vertically upward, and after refraction at the liquid surface, the beam travels along the surface of the liquid.
Step 2: Analyze Forces in the Accelerating Frame
In the accelerating frame of the liquid, we consider the effects of pseudo force. The forces acting on a small mass m of the liquid are:
- Gravitational force mg acting downward.
- Pseudo force ma acting horizontally in the opposite direction of acceleration.
Step 3: Establish the Angle of the Liquid Surface
At equilibrium, the forces must balance. The angle θ that the surface of the liquid makes with the horizontal can be determined using:
macosθ=mgsinθ
This simplifies to:
tanθ=ag
Substituting the given values:
tanθ=40310=43
Thus, θ=tan−1(43).
Step 4: Calculate the Angle θ
Using trigonometric values, we find:
θ≈53∘
Step 5: Refraction at the Liquid Surface
When the laser beam refracts at the liquid surface, it travels along the surface after refraction. According to Snell's Law:
μsini=nsinr
Where:
- μ is the refractive index of the liquid,
- i is the angle of incidence (which is θ),
- n is the refractive index of air (approximately 1),
- r is the angle of refraction (which is 90∘).
Since sin90∘=1, we can rewrite Snell's Law as:
μsinθ=1⋅1
Thus:
μ=1sinθ
Step 6: Calculate sinθ
From trigonometric ratios, we know:
sin53∘=45
Therefore:
μ=145=54=1.25
Final Answer
The refractive index of the liquid is:
μ=1.25
The tank is accelerating horizontally with an acceleration a=403m/s2. A laser pointer shoots a beam vertically upward, and after refraction at the liquid surface, the beam travels along the surface of the liquid.
In the accelerating frame of the liquid, we consider the effects of pseudo force. The forces acting on a small mass m of the liquid are:
- Gravitational force mg acting downward.
- Pseudo force ma acting horizontally in the opposite direction of acceleration.
At equilibrium, the forces must balance. The angle θ that the surface of the liquid makes with the horizontal can be determined using:
macosθ=mgsinθ
This simplifies to:
tanθ=ag
Substituting the given values:
tanθ=40310=43
Thus, θ=tan−1(43).
Using trigonometric values, we find:
θ≈53∘
When the laser beam refracts at the liquid surface, it travels along the surface after refraction. According to Snell's Law:
μsini=nsinr
Where:
- μ is the refractive index of the liquid,
- i is the angle of incidence (which is θ),
- n is the refractive index of air (approximately 1),
- r is the angle of refraction (which is 90∘).
μsinθ=1⋅1
Thus:
μ=1sinθ
From trigonometric ratios, we know:
sin53∘=45
Therefore:
μ=145=54=1.25
The refractive index of the liquid is:
μ=1.25
Similar Questions
When the rectangular metal tank is filled to the top with an unkown liquid, as observer with eyes level with the top of the tank can just see the corner E, a ray that refracts towards the observer at the top surface of the liquid is shown. The refractive index of the liquid will be

View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure ).
How fast is the light travelling in the liquid ?

View Solution
Knowledge Check
The height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
AHBH2C3H2D√3H2
A container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case

View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.
View SolutionA circular beam of light (diameter d) falls on a plane surface of a liquid. The angle of incidence is 45∘ and refractive index of the liquid is μ. The diameter of the refracted beam is
View SolutionA beaker containing liquid is placed on a table, underneath a microscope which can be moved along a vertical scale. The microscope is focused, through the liquid onto a mark on the table when the reading on the scale is a. It is next focused on the upper surface of the liquid and the reading is b. More liquid is added and the observations are repeated, the corresponding readings are c and d. The refractive index of the liquid is
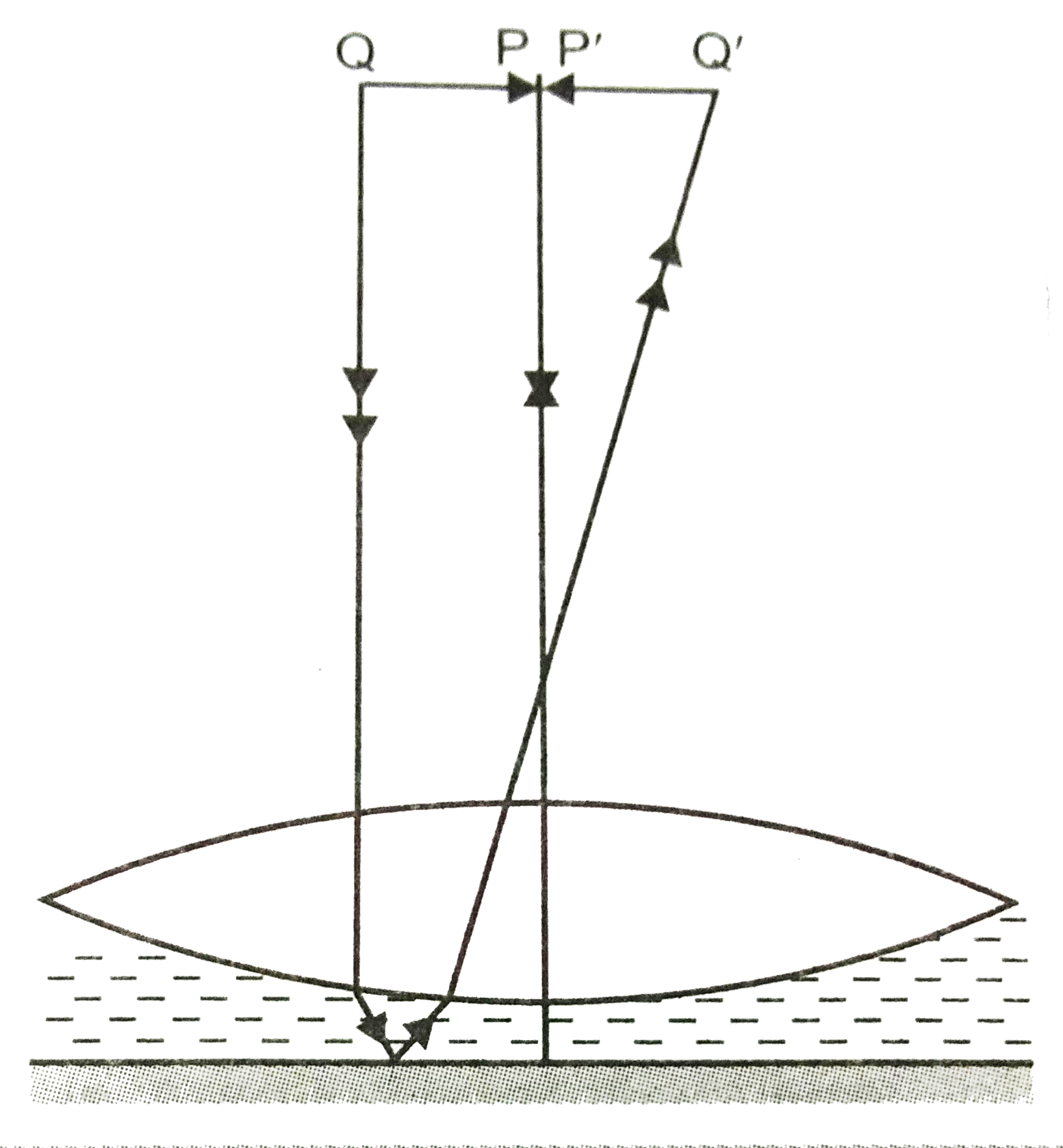
View SolutionFig. shows an equiconvex lens (of refractive index 1.5) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid ?
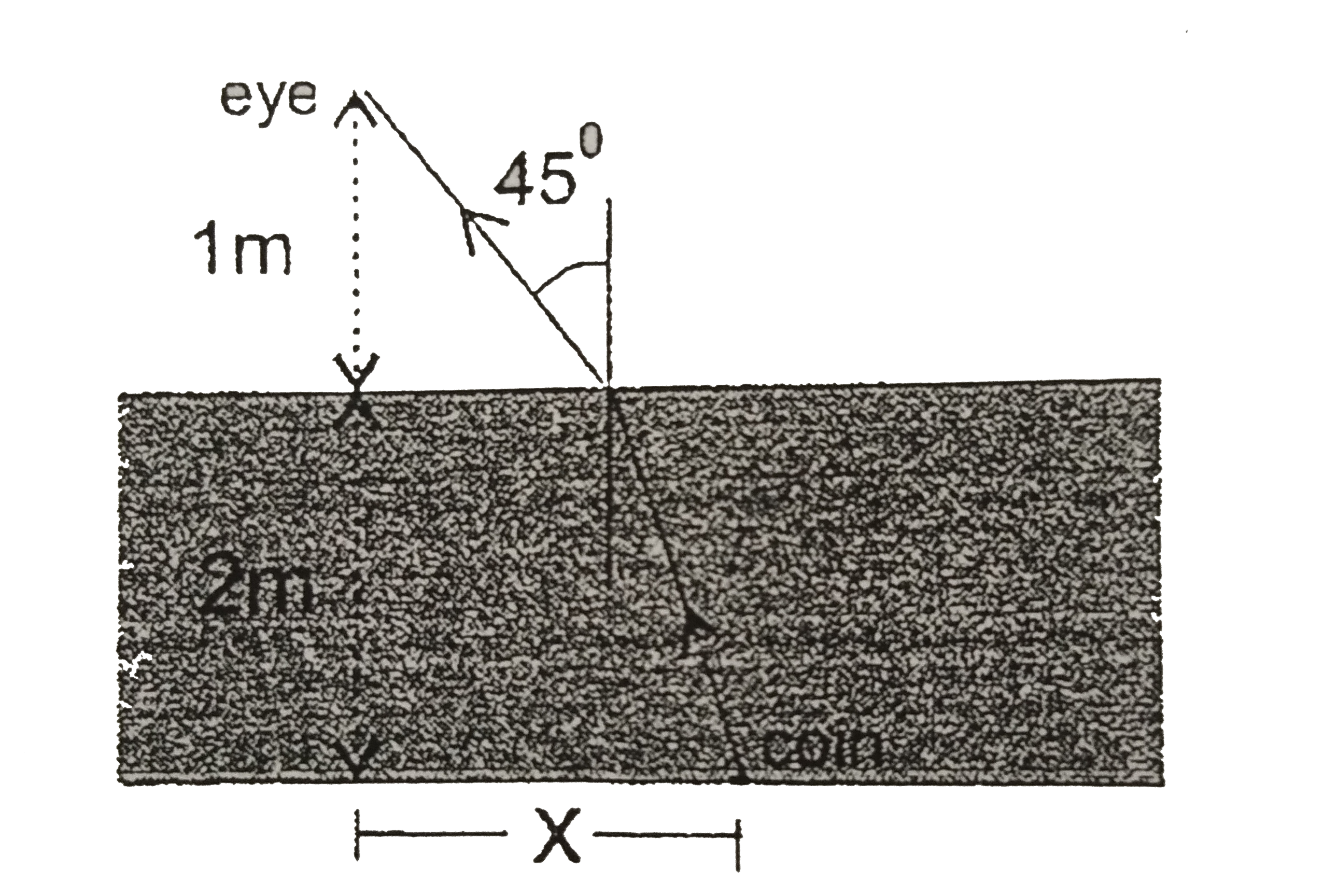
View SolutionA coin lies on the bottom of a lake 2m deep at a horizontal distance x from the spotlight (a source of thin parallel been of light) situated 1m above the surface of a liquid of refractive index μ=√2) and height 2m. Find x.
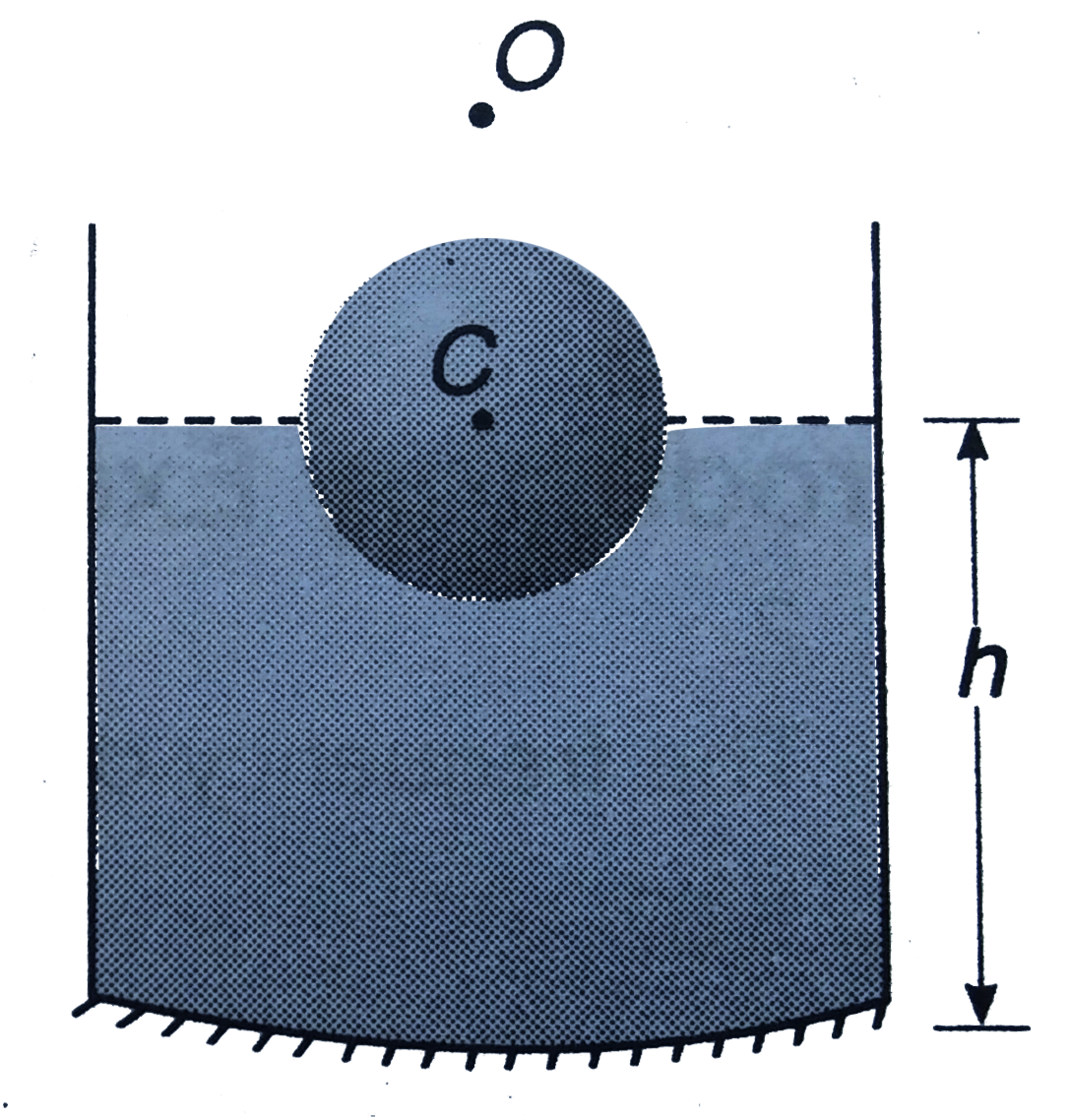
View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
View Solution
