A coin lies on the bottom of a lake 2m deep at a horizontal distance x from the spotlight (a source of thin parallel been of light) situated 1m above the surface of a liquid of refractive index μ=√2) and height 2m. Find x.
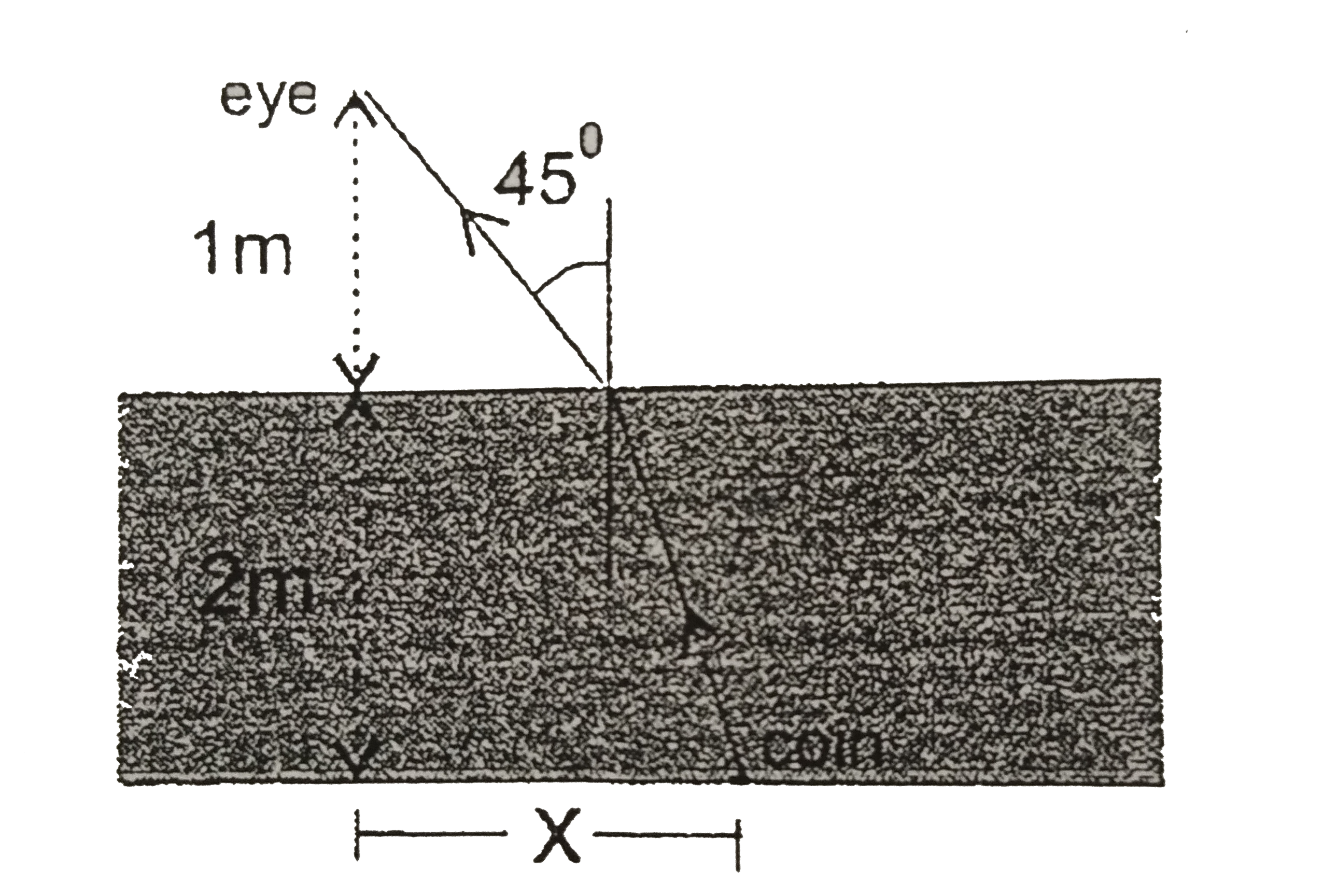
√2=sin45∘sinr
⇒sinr=12⇒r=30∘
x=RQ+QP
1m+2tan30∘m
=(1+2√3)m

Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-1141videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-262videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
Similar Questions
A double convex lens of refractive index m1 is immersed in a liquid of refractive index m2. This lens will act as:
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA pile 4m high driven into the bottom of a lake is 1m above the <br>water . Determine the length of the shadow of the pile on the bottom of the lake if <br> the sun rays make an angle of 45∘ with the water surface . The refractive index<br> if water is 43.
View SolutionA pile 4m high driven into the bottom of a lake is 1m above the <br>water . Determine the length of the shadow of the pile on the bottom of the lake if <br> the sun rays make an angle of 45∘ with the water surface . The refractive index<br> if water is 43.
View SolutionA disc is placed on a surface of pond which has refractive index 35 . A source of light is placed 4 m below the surface of liquid. The minimum radius of disc will be so light is not coming out
View SolutionThe speed of the yellow light in a certain liquid is2.4x108ms−1. Find the refractive index of the liquid.
View SolutionA point source of light is placed at a depth h=0.5 m below the surface of a liquid (μ=54) , Then , the fraction of light energy that escape directly from the liquid surface is
View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View SolutionA point source of light is placed at a distance h below the surface of a large and deep lake. Show that the fraction f of light that escape directly from water surface is independent of h and is given by
f=[1−√1−1/μ2]2View Solution

