A bullet of mass 20 g travelling horizontally at 100ms−1 gets embedded at the centre of a block of wood of mass 1kg, suspended by a light vertical string of 1m in length. Calculate the maximum inclination of the string to the vertical.
To solve the problem step by step, we will use the principles of conservation of momentum and conservation of energy.
Step 1: Conservation of Momentum
The bullet of mass m1=20g=0.02kg is traveling horizontally at a velocity v1=100m/s. The block of wood has a mass m2=1kg and is initially at rest (v2=0m/s).
Using the conservation of momentum:
m1v1+m2v2=(m1+m2)v
Substituting the values:
0.02×100+1×0=(0.02+1)v
2=1.02v
Solving for v:
v=21.02≈1.96m/s
Step 2: Conservation of Energy
Next, we apply the conservation of energy. The kinetic energy of the combined mass when the bullet is embedded in the block will be converted into potential energy at the maximum height.
The kinetic energy (KE) of the combined mass is given by:
KE=12(m1+m2)v2
Substituting the values:
KE=12×1.02×(1.96)2≈1.98J
The potential energy (PE) at the maximum height h is given by:
PE=(m1+m2)gh
Where g=9.81m/s2. Setting KE=PE:
1.98=1.02×9.81×h
Solving for h:
h=1.981.02×9.81≈0.2m
Step 3: Finding the Maximum Inclination
To find the angle θ at which the string inclines, we can use the relationship from the geometry of the situation. The length of the string L=1m and the height h=0.2m.
Using the cosine relation:
cosθ=adjacenthypotenuse=L−hL=1−0.21=0.8
Thus,
θ=cos−1(0.8)
Calculating θ:
θ≈36.87∘≈37∘
Final Answer
The maximum inclination of the string to the vertical is approximately 37∘.
The bullet of mass m1=20g=0.02kg is traveling horizontally at a velocity v1=100m/s. The block of wood has a mass m2=1kg and is initially at rest (v2=0m/s).
m1v1+m2v2=(m1+m2)v
Substituting the values:
0.02×100+1×0=(0.02+1)v
2=1.02v
Solving for v:
v=21.02≈1.96m/s
Next, we apply the conservation of energy. The kinetic energy of the combined mass when the bullet is embedded in the block will be converted into potential energy at the maximum height.
KE=12(m1+m2)v2
Substituting the values:
KE=12×1.02×(1.96)2≈1.98J
PE=(m1+m2)gh
Where g=9.81m/s2. Setting KE=PE:
1.98=1.02×9.81×h
Solving for h:
h=1.981.02×9.81≈0.2m
To find the angle θ at which the string inclines, we can use the relationship from the geometry of the situation. The length of the string L=1m and the height h=0.2m.
cosθ=adjacenthypotenuse=L−hL=1−0.21=0.8
Thus,
θ=cos−1(0.8)
Calculating θ:
θ≈36.87∘≈37∘
The maximum inclination of the string to the vertical is approximately 37∘.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
14 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE
37 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-H (MULTIPLE TRUE FALSE TYPE QUESTIONS)
10 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View Solution
Knowledge Check
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
A bullet of mass 0.02 kg travelling horizontally with velocity 250ms−1 strikes a block of wood of mass 0.23 kg which rests on a rough horizontal surface. After the impact, the block and bullet move together and come to rest after travelling a distance of 40m. The coefficient of sliding friction of the rough surface is (g=9.8ms_2)
View SolutionA mass M kg is suspended by a weightless string. The horizontal force required to hold the mass at 60∘ with the vertical is
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
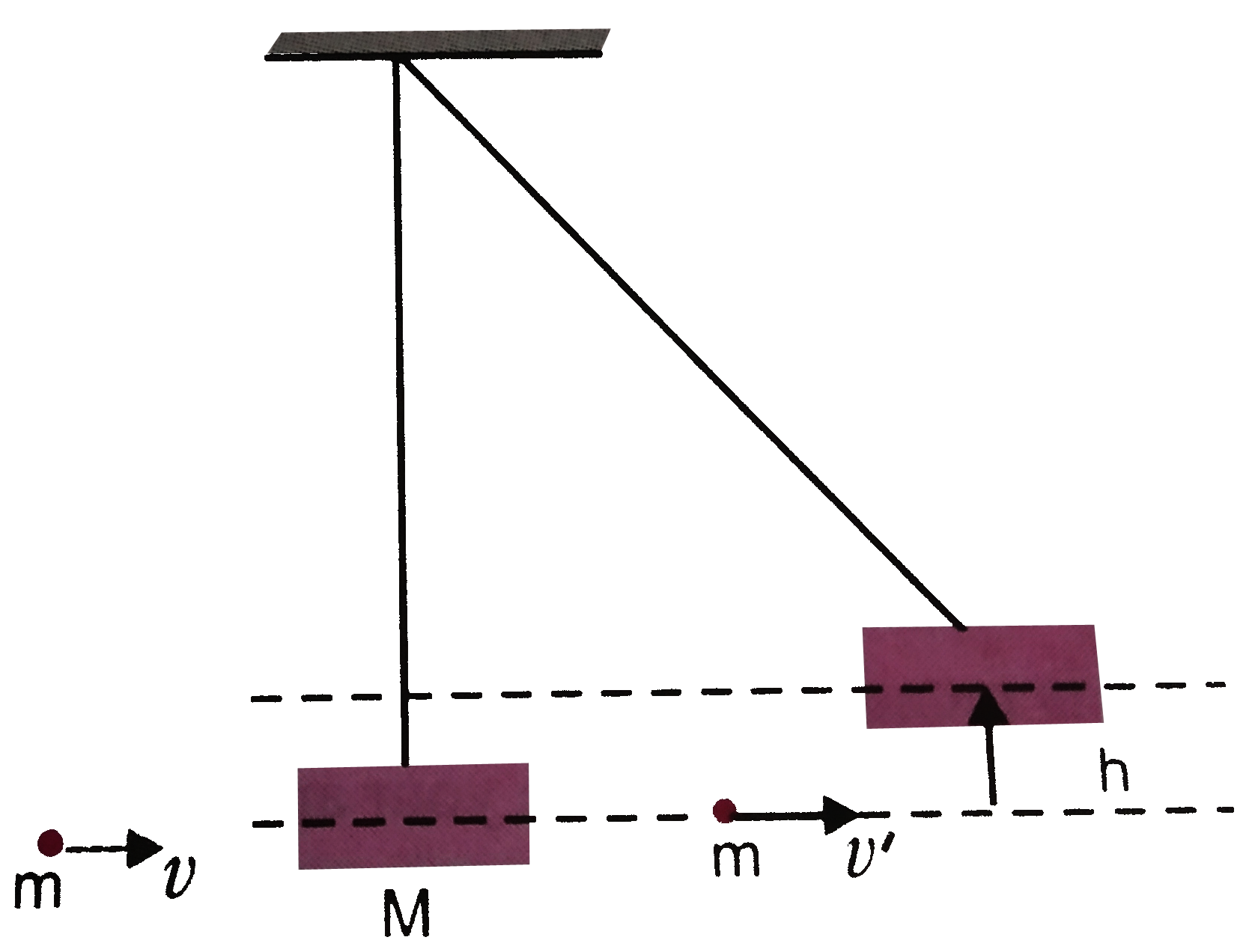
View SolutionA bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA bullet of mass 2g travelling at a speed of 500m/s is fired into a ballistic pendulum of mass 1.0kg suspended from a cord 1.0m long. The bullet penetrates the pendulum and emerges with a velocity of 100m/s. Through what vertical height will the pendulum rise?
View Solution
