If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the trisection which also the points of trisection of DP and BQ respectively.
To prove that the lines DP and BQ cut the diagonal AC of the parallelogram ABCD at points that are also the trisection points of DP and BQ, we can follow these steps:
Step 1: Set up the parallelogram and define the points
Let A, B, C, and D be the vertices of the parallelogram ABCD. We can assign position vectors to these points:
- Let the position vector of point A be →A=→0 (taking A as the origin).
- Let the position vector of point B be →B.
- Let the position vector of point D be →D.
- Since ABCD is a parallelogram, the position vector of point C will be →C=→B+→D.
Step 2: Find the midpoints P and Q
The midpoints P and Q of sides AB and CD respectively can be calculated as follows:
- The position vector of midpoint P (of AB) is given by:
→P=→A+→B2=→0+→B2=→B2
- The position vector of midpoint Q (of CD) is given by:
→Q=→C+→D2=(→B+→D)+→D2=→B+2→D2
Step 3: Find the points of trisection of DP and BQ
Next, we find the points that trisect the segments DP and BQ.
For DP:
Let the point dividing DP in the ratio 2:1 be denoted as R. Using the section formula:
→R=2→D+1→P2+1=2→D+→B23=4→D+→B6
For BQ:
Let the point dividing BQ in the ratio 2:1 be denoted as S. Again using the section formula:
→S=2→Q+1→B2+1=2(→B+2→D2)+→B3=→B+2→D+→B3=2→B+2→D3=2(→B+→D)3
Step 4: Find the point of intersection of DP and BQ
We need to show that points R and S coincide with the trisection point of the diagonal AC.
The diagonal AC can be expressed as:
→A+t(→C−→A)=t(→B+→D)for t∈(0,1)
The trisection points of AC can be found at t=13 and t=23:
- For t=13:
→T1=13(→B+→D)
- For t=23:
→T2=23(→B+→D)
Step 5: Show that R and S coincide with T1 and T2
From our calculations:
- The point R (trisection of DP) is 4→D+→B6=13(→B+→D).
- The point S (trisection of BQ) is 2(→B+→D)3.
Thus, we conclude that:
- DP cuts AC at the trisection point T1.
- BQ cuts AC at the trisection point T2.
Conclusion
Therefore, we have proved that the lines DP and BQ cut the diagonal AC at points that are also the trisection points of DP and BQ respectively.
---
Let A, B, C, and D be the vertices of the parallelogram ABCD. We can assign position vectors to these points:
- Let the position vector of point A be →A=→0 (taking A as the origin).
- Let the position vector of point B be →B.
- Let the position vector of point D be →D.
- Since ABCD is a parallelogram, the position vector of point C will be →C=→B+→D.
The midpoints P and Q of sides AB and CD respectively can be calculated as follows:
- The position vector of midpoint P (of AB) is given by:
→P=→A+→B2=→0+→B2=→B2
- The position vector of midpoint Q (of CD) is given by:
→Q=→C+→D2=(→B+→D)+→D2=→B+2→D2
Next, we find the points that trisect the segments DP and BQ.
Let the point dividing DP in the ratio 2:1 be denoted as R. Using the section formula:
→R=2→D+1→P2+1=2→D+→B23=4→D+→B6
Let the point dividing BQ in the ratio 2:1 be denoted as S. Again using the section formula:
→S=2→Q+1→B2+1=2(→B+2→D2)+→B3=→B+2→D+→B3=2→B+2→D3=2(→B+→D)3
We need to show that points R and S coincide with the trisection point of the diagonal AC.
→A+t(→C−→A)=t(→B+→D)for t∈(0,1)
The trisection points of AC can be found at t=13 and t=23:
- For t=13:
→T1=13(→B+→D)
- For t=23:
→T2=23(→B+→D)
From our calculations:
- The point R (trisection of DP) is 4→D+→B6=13(→B+→D).
- The point S (trisection of BQ) is 2(→B+→D)3.
- DP cuts AC at the trisection point T1.
- BQ cuts AC at the trisection point T2.
Therefore, we have proved that the lines DP and BQ cut the diagonal AC at points that are also the trisection points of DP and BQ respectively.
Similar Questions
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionX and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Prove that □AXCY is a parallelogram.
View SolutionP and Q are the mid-point of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PQRS is a parallelogram.
 View Solution
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP.
View SolutionM and N are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CN is parallel to AM.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ
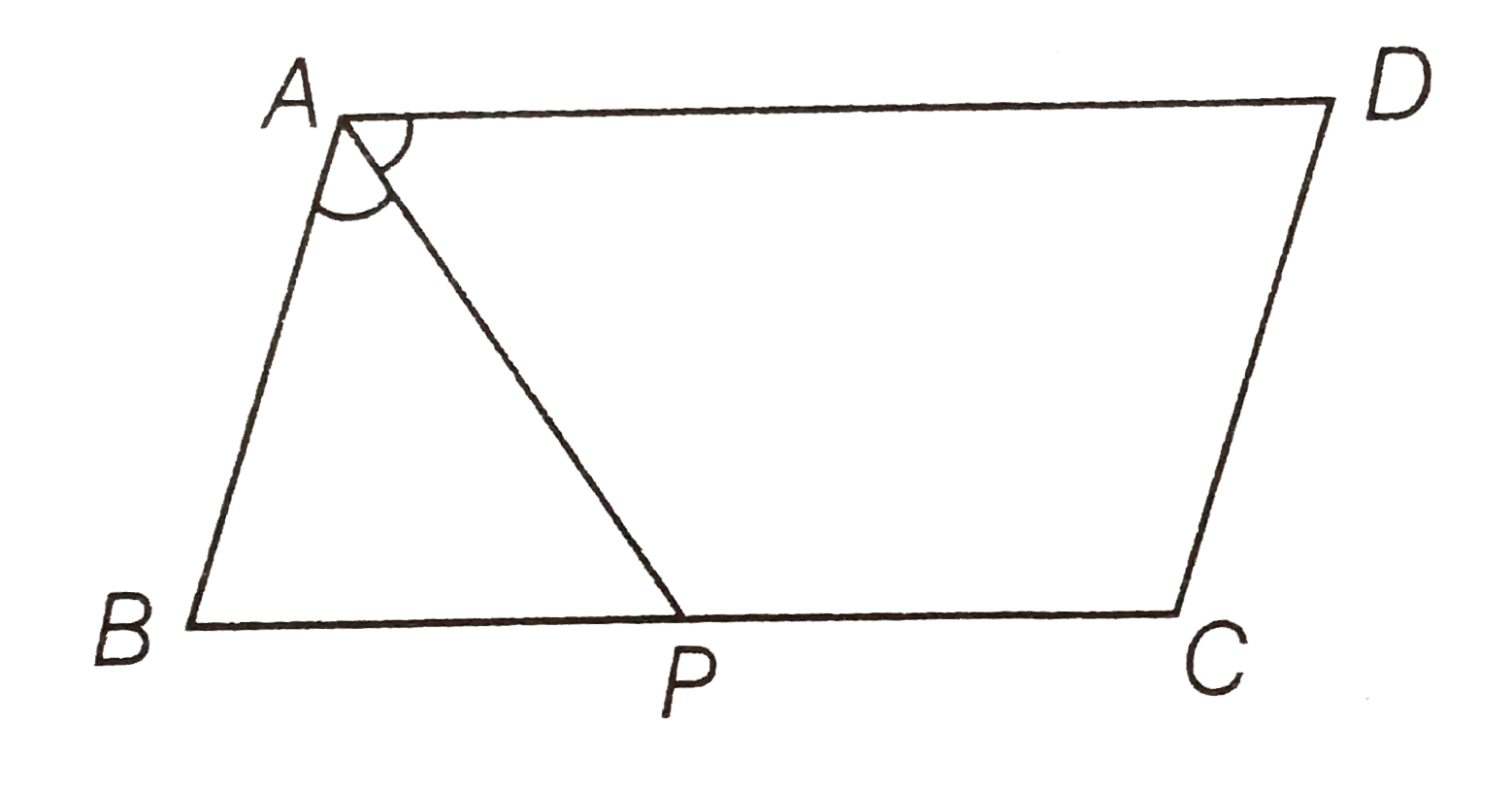
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD.
 View Solution
View SolutionE is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD . Prove that AEFD is a parallelogram.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.View Solution

