If G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
The correct Answer is:3(GA2+GB2+GC2)
Step by step video & image solution for If G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionAD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionIn a tetrahedron OABC, the edges are of lengths, |OA|=|BC|=a,|OB|=|AC|=b,|OC|=|AB|=c. Let G1andG2 be the centroids of the triangle ABC and AOC such that OG1⊥BG2, then the value of a2+c2b2 is
View Solutionlf G be the centroid of a triangle ABC and P be any other point in the plane prove that PA2+PB2+PC2=GA2+GB2+GC2+3GP2
View SolutionIf G is the centroid of a ΔABC, then GA2+GB2+GC2 is equal to
View SolutionIn the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB repectively of triangle ABC. Prove that :
AR2+BP2+CQ2=AQ2+CP2+BR2
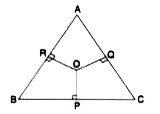
View SolutionIf G is the centroid of △ABC,prove that −−→GA+−−→GB+−−→GC=0. Further if G1 bet eh centroid of another △PQR, show that −−→AP+−−→BQ+−−→CR=3−−−→GG1
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionIf G is the centroid of triangle with vertices A(a,0),B(−a,0) and C(b,c) then AB2+BC2+CA2GA2+GB2+GC2=
View Solution
