A stick of length 10 units rests against the floor and a wall of a room. If the stick begins to slide ontfloor then the locus of its middle point is:
The correct Answer is:l2
To solve the problem, we need to find the locus of the midpoint of a stick of length 10 units that is resting against the floor and a wall. Let's denote the endpoints of the stick as points A and B.
1. Define the Coordinates:
- Let point A be at coordinates (a, 0) on the floor (x-axis).
- Let point B be at coordinates (0, b) on the wall (y-axis).
- The stick forms a right triangle with the floor and the wall.
2. Midpoint Calculation:
- The midpoint M of the stick AB can be calculated using the midpoint formula:
M=(a+02,0+b2)=(a2,b2)
- Let the coordinates of the midpoint M be (h, k), so:
h=a2andk=b2
3. Length of the Stick:
- The length of the stick is given as 10 units. According to the distance formula, we have:
AB=√(a−0)2+(b−0)2=10
- Squaring both sides gives:
a2+b2=100
4. Substituting for a and b:
- From the expressions for h and k, we can express a and b in terms of h and k:
a=2handb=2k
- Substituting these into the equation a2+b2=100:
(2h)2+(2k)2=100
- Simplifying this gives:
4h2+4k2=100
- Dividing through by 4:
h2+k2=25
5. Final Locus Equation:
- The equation h2+k2=25 represents a circle with a radius of 5 units centered at the origin (0, 0).
- Therefore, the locus of the midpoint of the stick as it slides is a circle with radius 5.
Final Answer:
The locus of the midpoint of the stick is given by the equation:
x2+y2=25
- Let point A be at coordinates (a, 0) on the floor (x-axis).
- Let point B be at coordinates (0, b) on the wall (y-axis).
- The stick forms a right triangle with the floor and the wall.
- The midpoint M of the stick AB can be calculated using the midpoint formula:
M=(a+02,0+b2)=(a2,b2)
- Let the coordinates of the midpoint M be (h, k), so:
h=a2andk=b2
- The length of the stick is given as 10 units. According to the distance formula, we have:
AB=√(a−0)2+(b−0)2=10
- Squaring both sides gives:
a2+b2=100
- From the expressions for h and k, we can express a and b in terms of h and k:
a=2handb=2k
- Substituting these into the equation a2+b2=100:
(2h)2+(2k)2=100
- Simplifying this gives:
4h2+4k2=100
- Dividing through by 4:
h2+k2=25
- The equation h2+k2=25 represents a circle with a radius of 5 units centered at the origin (0, 0).
- Therefore, the locus of the midpoint of the stick as it slides is a circle with radius 5.
The locus of the midpoint of the stick is given by the equation:
x2+y2=25
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Column I, Column II stick of length 10 units rests against the floor and a wall of a room. If the stick begins to slide on the floor then the locus of its middle point is (Assume the origin to be the intersection of the floor and the wall and the coordinate axes along the floor and the wall), p. √6 ∀′ is the major axis of the ellipse 3x2+2y2+6x−4y−1=0 and P is a variable point on it. Then the greatest area of triangle APA' is, q. 2√7 The distance between the foci of the curve represented by the equation x=1+4cosθ,y=2+3sinθ is, r. 1283 Tangents are drawn to the ellipse x216+y27=1 at the endpoints of the latus rectum. The area of the quadrilateral so formed is, s. √5
View SolutionA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
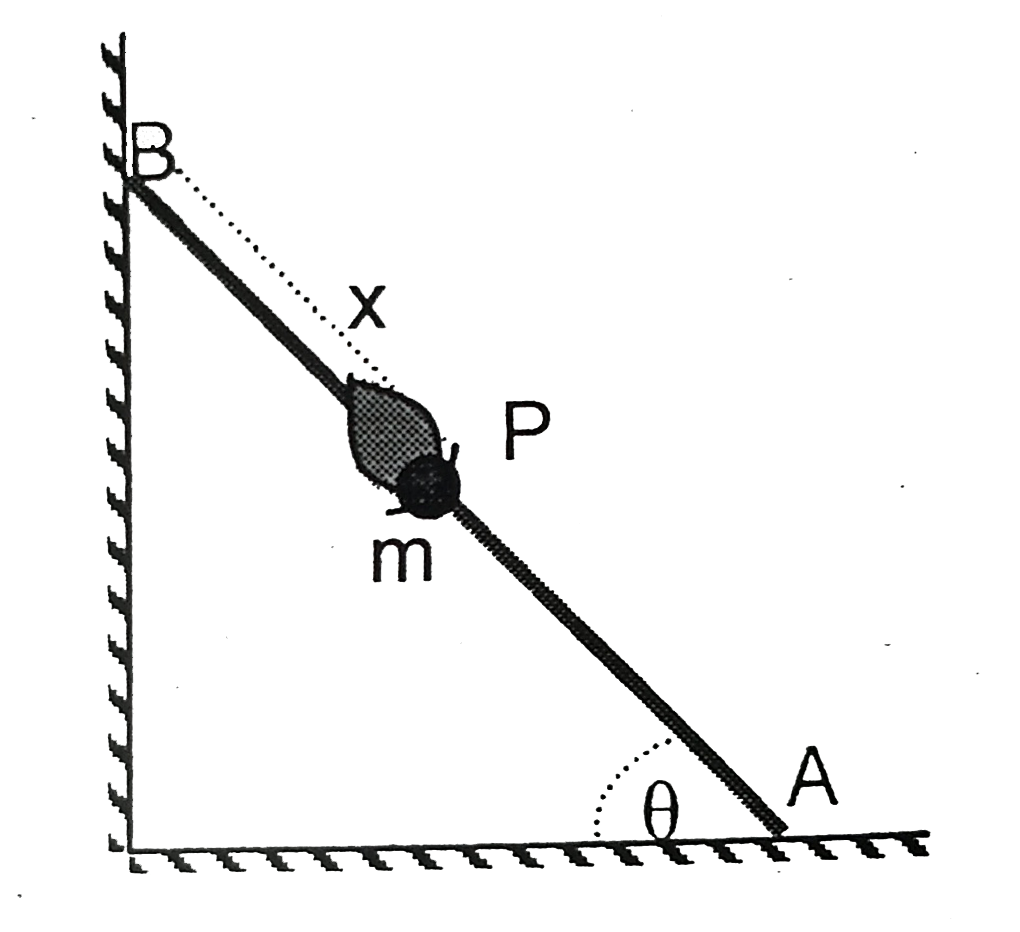
View SolutionA rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View SolutionA rod of AB of length 3 rests on a wall as follows :
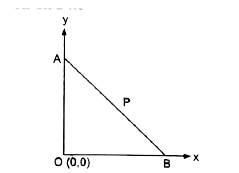
P is a point on AB such that AP:PB=1:2 If the rod slides along the wall, then the locus of P lies on
View SolutionThe top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance? How far is the foot from the wall when it and the top are moving at the same rate?
View SolutionThe top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance? How far is the foot from the wall when it and the top are moving at the same rate?
View SolutionA uniform wooden stick of mass 1.6 kg and length l rests in an inclined mannar on a smooth, vertical wall of height h(<l) such that a small portion of the stick extends beyond the wall. The reaction force of th wall on the stick is perpendicular to the stick. The stick makes an angle of 30∘ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/l and the friectional force f at the bottom of the stick are (g=10ms2)
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
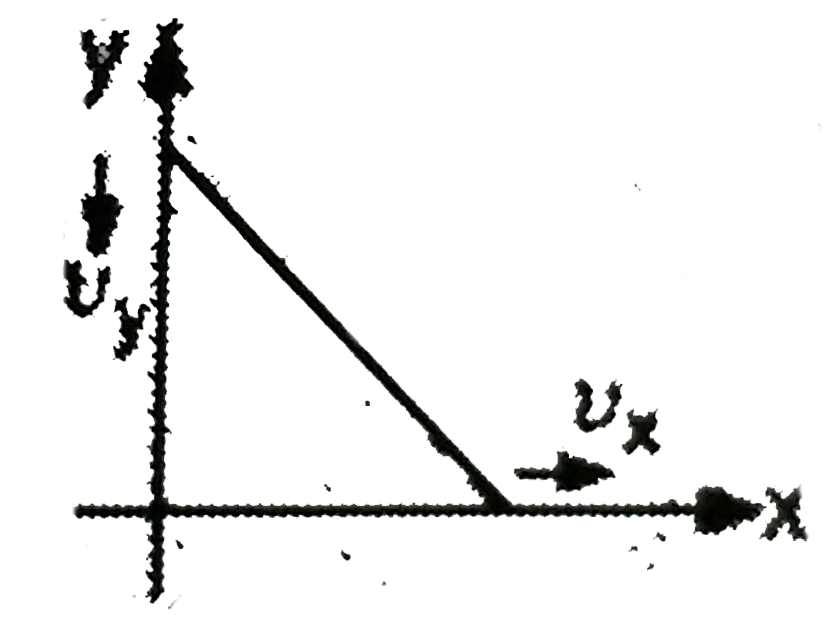
View SolutionA massless stick of length L is hinged at one end and a mass m attached to its other end. The stick is free to rotate in vertical plane about a fixed horizontal axis passing through frictionless hinge. The stick is held in a horizontal position. At what distance x from the hinge should a second mass M = m be attached to the stick, so that stick falls as fast as possible when released from rest

View SolutionIn a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
View Solution
