If the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
The correct Answer is:A1A2=πr252r2cos18∘=2π5sec(π10)
Step by step video & image solution for If the area of the circle is A_1 and the area of the regular pentagon inscribed in the circle is A_2, then find the ratio (A_1)/(A_2)dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
A body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
A0.21458333333333B0.21319444444444C0.37847222222222D0.37986111111111
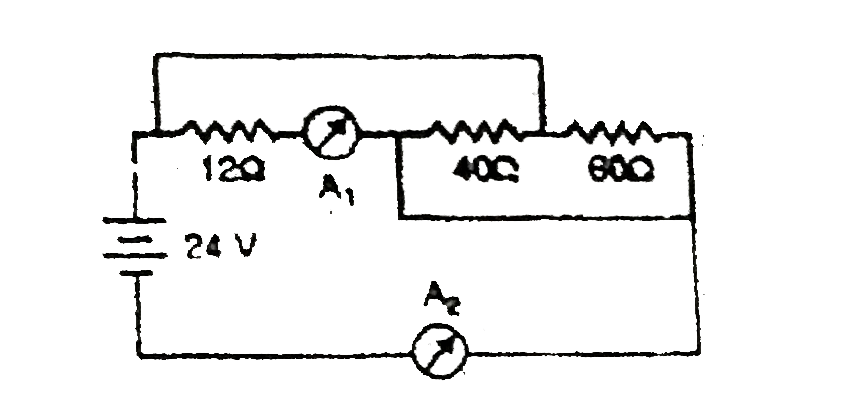
In the circuit of figure A1 and A2 are ideal ammeters. Then the reading in ammeter A2 is
View SolutionA circle is inscribed inside a regular pentagon and another circle is circumscribed about this pentagon.Similarly a circle is inscribed in a regular heptagon and another circumscribed about the heptagon. The area of the regions between the two circles in two cases are A1andA2, respectively. If each polygon has a side length of 2 units then which one of the following is true?
View SolutionIf A,A1,A2 and A3 are the areas of the inscribed and escribed circles of a triangle, prove that 1√A=1√A1+1√A2+1√A3
View SolutionIf A1 is the area of the parabola y2=4ax lying between vertex and the latusrectum and A2 is the area between the latusrectum and the double ordinate x=2a, then A1A2 is equal to
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
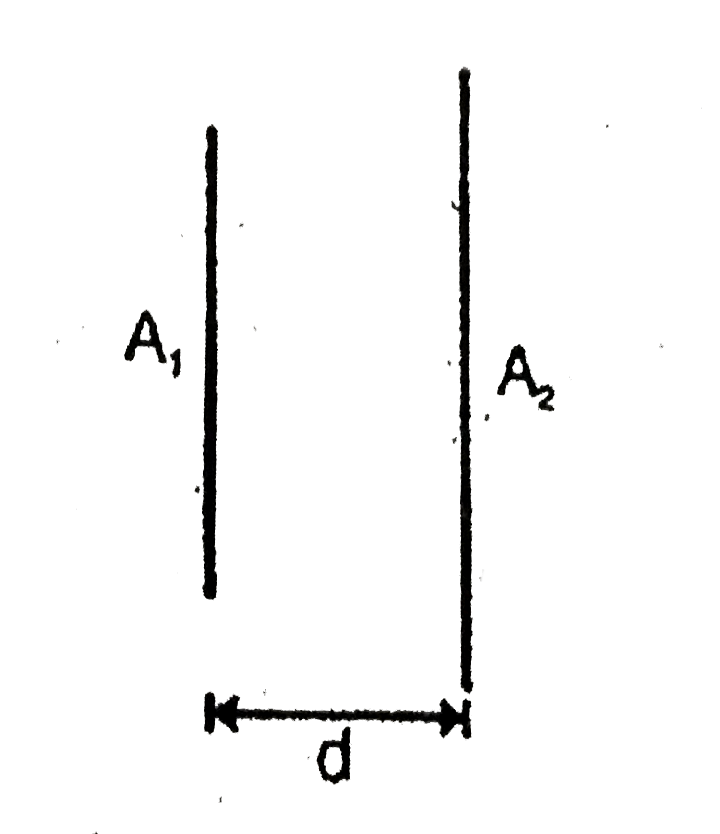
View SolutionThe capacitance of capacitor of plate areas A1 and A2 (A1<A2 at a distance d is

View SolutionLet Ar,r=1,2,3, , be the points on the number line such that OA1,OA2,OA3. are in GP, where O is the origin, and the common ratio of the GP be a positive proper fraction. Let M, be the middle point of the line segment ArAr+1. Then the value of ∞∑r=1OMr is equal to
(a) OA1(OSA1−OA2)2(OA1+OA2) (b) OA1(OA2+OA1)2(OA1−OA2) (c)OA12(OA1−OA2) (d) ∞
View Solution
