If (e1,e2,e3) and (e'1,e'2,e'3) are two sets of non-coplanar vectors such that i=1,2,3 we have ei.e'j={1,ifi=j∣0,ifi≠j} then show that [e1e2e3][e'1e'2e'3]=1
To show that (e1,e2,e3)(e′1,e′2,e′3)=1, we will use the properties of the dot product and the determinant of vectors. The notation (e1,e2,e3) represents the scalar triple product of the vectors e1,e2,e3.
1. Understanding the Given Condition:
We are given that ei⋅e′j=1 if i=j and 0 if i≠j. This means that the vectors e1,e2,e3 are orthonormal to the vectors e′1,e′2,e′3.
2. Setting Up the Matrix:
We can represent the vectors e1,e2,e3 and e′1,e′2,e′3 in matrix form. Let:
E=⎛⎜⎝ex1ey1ez1ex2ey2ez2ex3ey3ez3⎞⎟⎠
and
E′=⎛⎜
⎜⎝e′x1e′y1e′z1e′x2e′y2e′z2e′x3e′y3e′z3⎞⎟
⎟⎠
3. Calculating the Product:
The product (e1,e2,e3)(e′1,e′2,e′3) can be computed as the determinant of the matrix formed by combining E and E′:
Det(E⋅E′)=∣∣
∣
∣∣ex1ey1ez1ex2ey2ez2ex3ey3ez3∣∣
∣
∣∣⋅⎛⎜
⎜⎝e′x1e′y1e′z1e′x2e′y2e′z2e′x3e′y3e′z3⎞⎟
⎟⎠
4. Evaluating the Determinant:
The determinant of the product of two matrices can be expressed as the product of their determinants:
Det(E)⋅Det(E′)
Since E and E′ are orthonormal bases, we have:
Det(E)=1andDet(E′)=1
5. Final Result:
Therefore, we conclude:
(e1,e2,e3)(e′1,e′2,e′3)=Det(E)⋅Det(E′)=1⋅1=1
Conclusion:
Thus, we have shown that (e1,e2,e3)(e′1,e′2,e′3)=1.
---
We are given that ei⋅e′j=1 if i=j and 0 if i≠j. This means that the vectors e1,e2,e3 are orthonormal to the vectors e′1,e′2,e′3.
We can represent the vectors e1,e2,e3 and e′1,e′2,e′3 in matrix form. Let:
E=⎛⎜⎝ex1ey1ez1ex2ey2ez2ex3ey3ez3⎞⎟⎠
and
E′=⎛⎜
⎜⎝e′x1e′y1e′z1e′x2e′y2e′z2e′x3e′y3e′z3⎞⎟
⎟⎠
The product (e1,e2,e3)(e′1,e′2,e′3) can be computed as the determinant of the matrix formed by combining E and E′:
Det(E⋅E′)=∣∣
∣
∣∣ex1ey1ez1ex2ey2ez2ex3ey3ez3∣∣
∣
∣∣⋅⎛⎜
⎜⎝e′x1e′y1e′z1e′x2e′y2e′z2e′x3e′y3e′z3⎞⎟
⎟⎠
The determinant of the product of two matrices can be expressed as the product of their determinants:
Det(E)⋅Det(E′)
Since E and E′ are orthonormal bases, we have:
Det(E)=1andDet(E′)=1
Therefore, we conclude:
(e1,e2,e3)(e′1,e′2,e′3)=Det(E)⋅Det(E′)=1⋅1=1
Thus, we have shown that (e1,e2,e3)(e′1,e′2,e′3)=1.
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - JEE Type Solved Examples: Passage Based Type Questions
3 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 1
12 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
If →e1,→e2,→e3and→E1,→E2,→E3 are two sets of vectors such that →et→Ej=1,ifi=j and →et→Ej=0andifi≠j, then prove that [→e1→e2→e3][→E1→E2→E3]=1.
View SolutionIf →e1,→e2,→e3and→E1,→E2,→E3 are two sets of vectors such that →et→Ej=1,ifi=jand→et→Ej=0andifi≠j, then prove that [→e1→e2→e3][→E1→E2→E3]=1.
View SolutionSuppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
P(none of E1,E2,E3) equals
View SolutionIf E1 and E2 are two events such that P(E1)=1/4, P(E2/E1)=1/2 and P(E1/E2)=1/4, then
View SolutionIf e1,e2,e3 and e4 are the four elementary outcomes in a sample space and P(e1)=0.1,P(e2)=0.5,and P(e3)=0.1, then the probability of e4 is ……
View SolutionIf E and F are events such that P(E)=14,P(F)=12andP(EandF)=18, find (i) P(EorF), (ii) P(−Eand−F).
View SolutionSuppose E1,E2andE3 be three mutually exclusive events such that P(Ei)=pi for i=1,2,3.
If p1,p2andp3 are the roots of 27x3−27x2+ax−1=0 the value of a is
View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
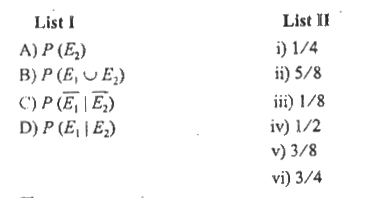
The correct matching of the list I from the list II is :
View SolutionStatement-I 53and54 are the eccentricities of two conjugate hyperbolas.
Statement-II If e1ande2 are the eccentricities of two conjugate hyperbolas, then e1e2>1.
View SolutionCharge Q is given a displacement →r=aˆi+bˆj in an electric field →E=E1ˆi+E2ˆj. The work done is.
View Solution
