In the given diagram ABCD is a parallelogram. ΔAPD and ΔBQC are equilateral triangles.
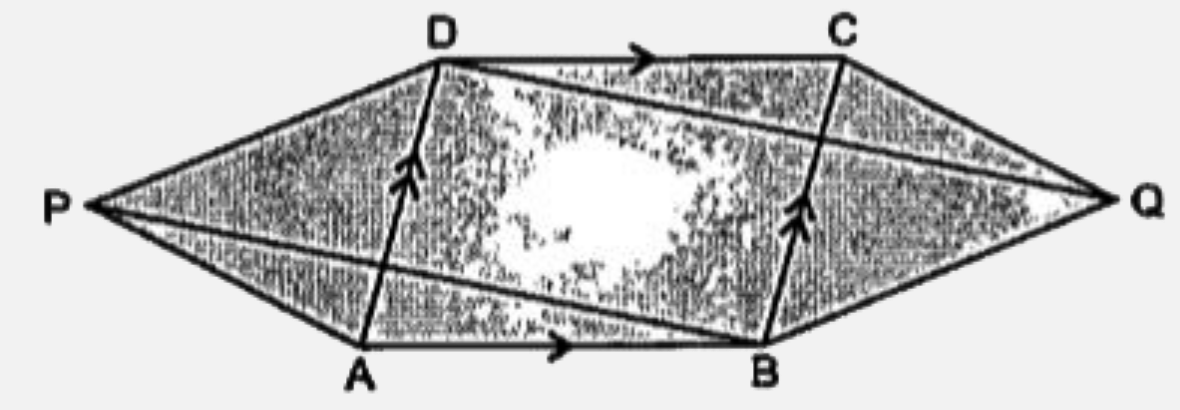
Prove that :
∠PAB=∠QCD
The correct Answer is:∠PAB=∠QCD
Step by step video & image solution for In the given diagram ABCD is a parallelogram. DeltaAPD and DeltaBQC are equilateral triangles. Prove that : anglePAB=angleQCD by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In the given diagram ABCD is a parallelogram. ΔAPD and ΔBQC are equilateral triangles.
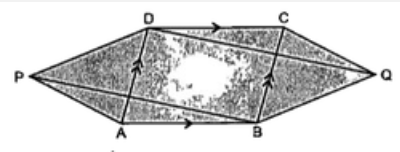
Prove that :
PB=QDView SolutionIn the given figure ABCD is a parallelogram. Prove that AB = 2BC.
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
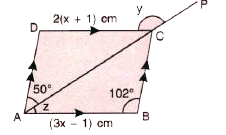 View Solution
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
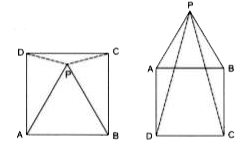 View Solution
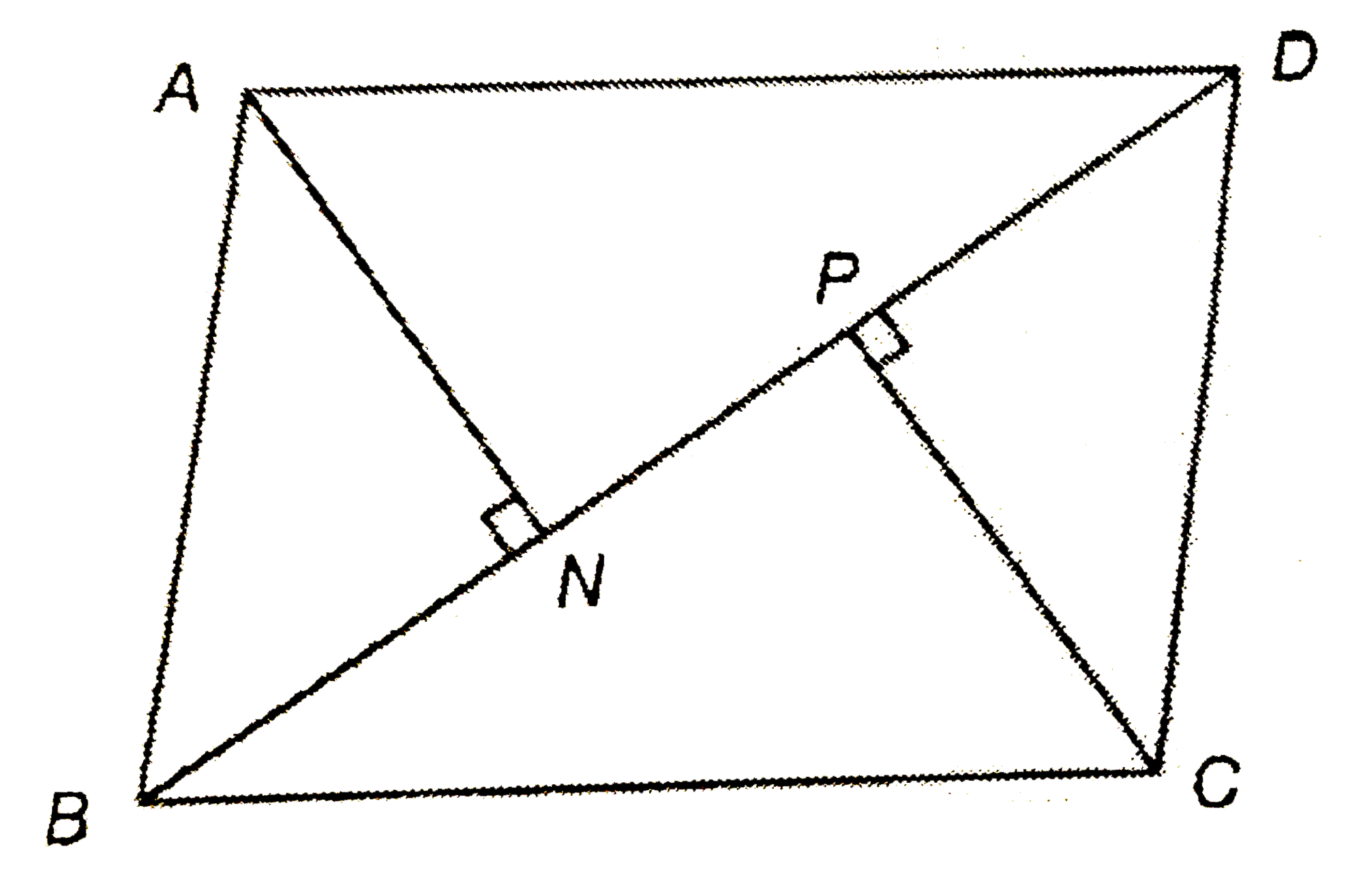
View SolutionIn the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
 View Solution
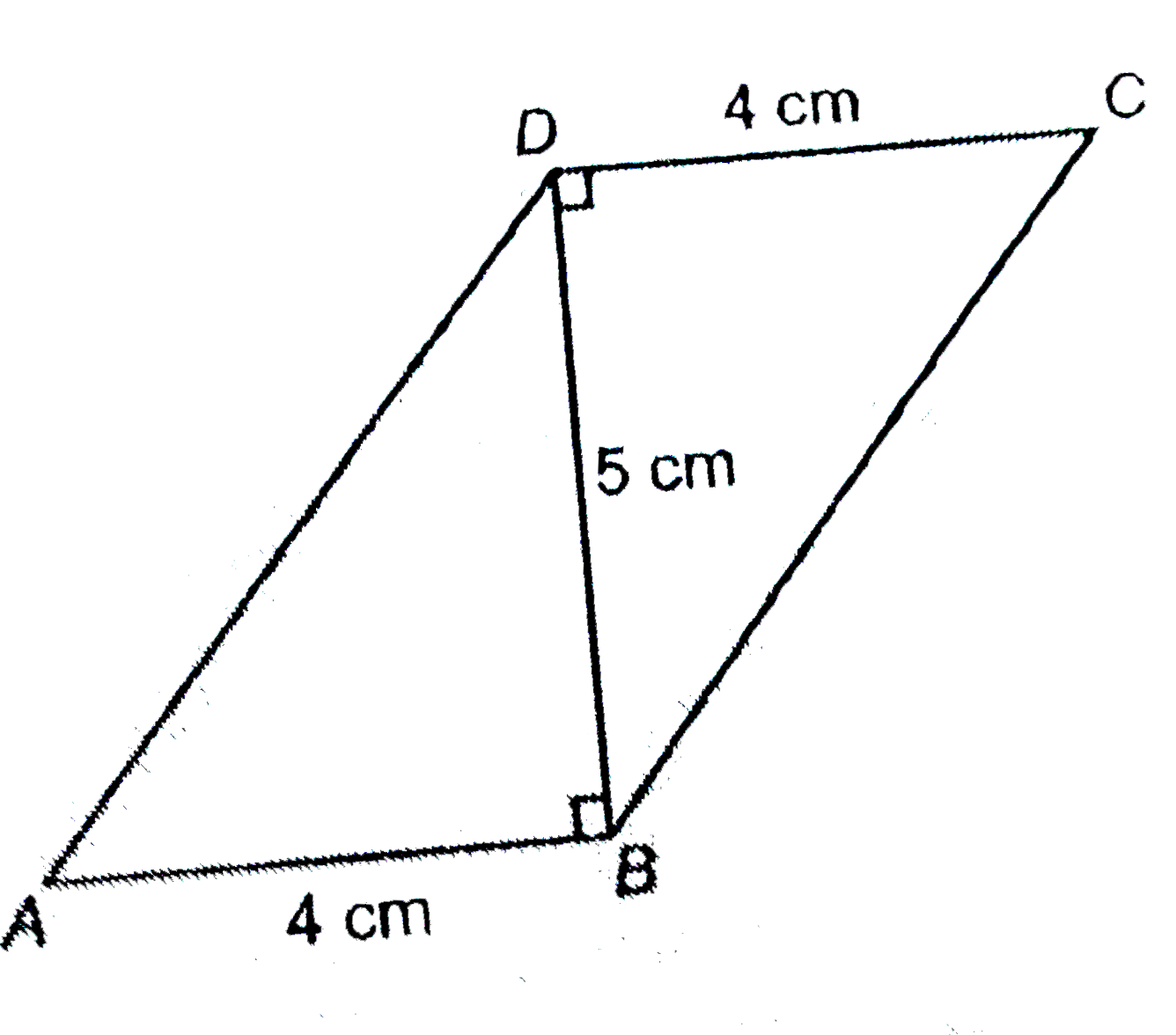
View SolutionIn the following figure, ABCD is a parallelogram. Prove that:

BP bisects angle BView SolutionIn the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
 View Solution
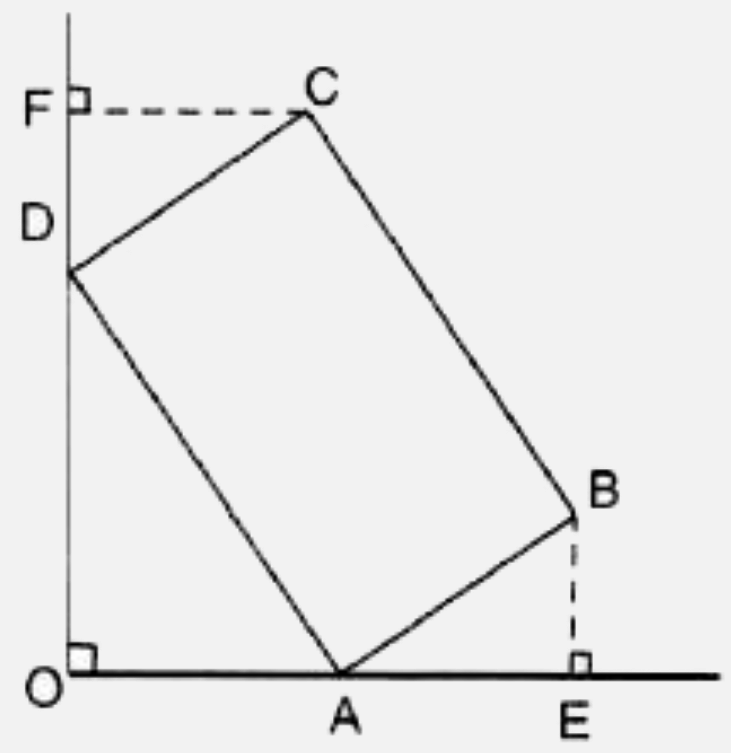
View SolutionIn the given figures , ABCD is a rectangle
Prove that : ΔABE≅ΔCDF.
 View Solution
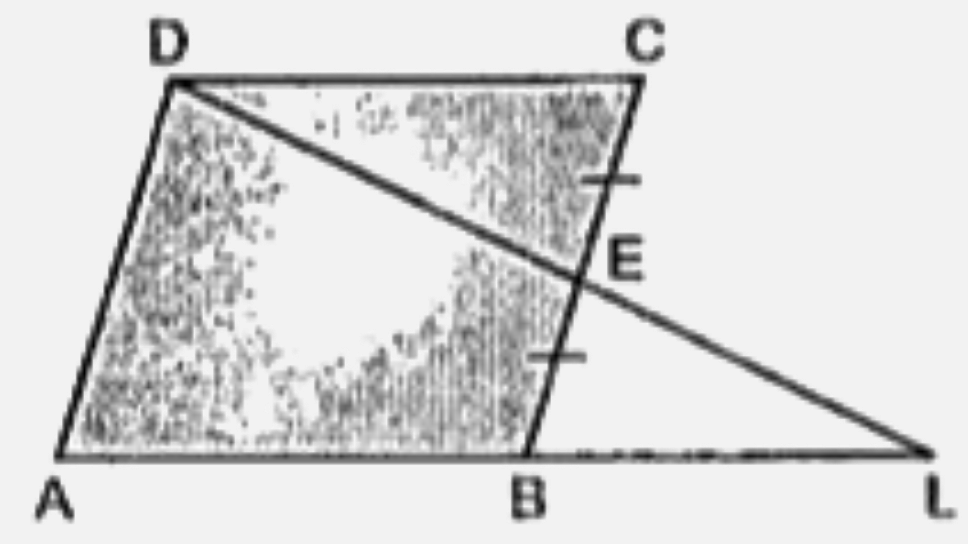
View SolutionFrom the given diagram, in which ABCD is a Parallelogram, ABL is a line segment and E is a mid - point of BC.
Prove that :
AB=BL
 View Solution
View Solution

