In the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
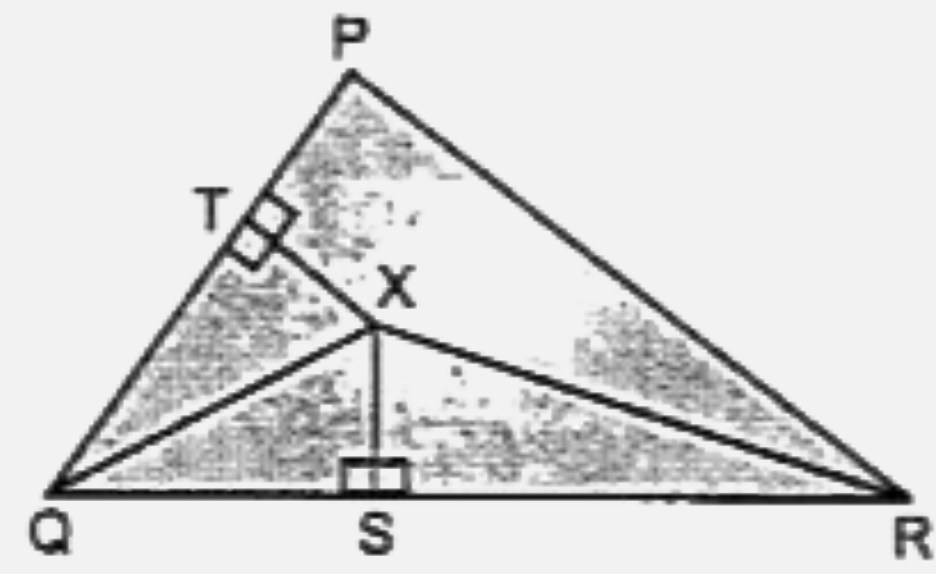
Prove that :
ΔXTQ≅ΔXSQ
The correct Answer is:XT=XS
Step by step video & image solution for In the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS bot QR and XTbotPQ. Prove that : DeltaXTQ~=DeltaXSQ by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 3 MARKS QUESTIONS
11 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
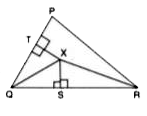
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS⊥QRandXT⊥PQ, prove that :
ΔXTQ≅ΔXSQ
View SolutionIn the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
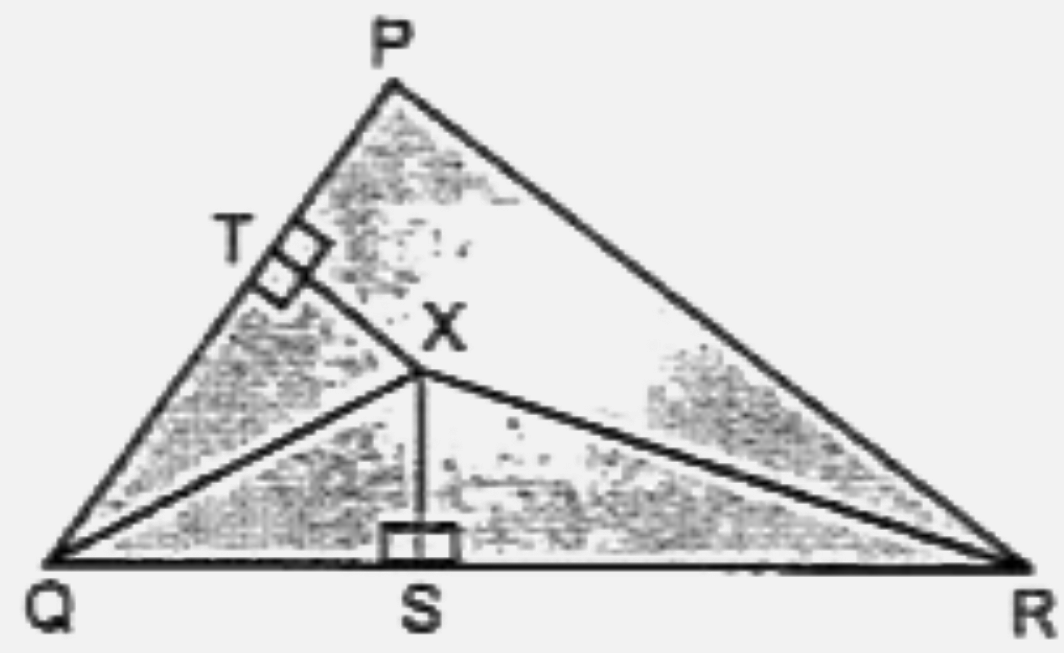
Prove that :
PX bisects angle P.
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.

View SolutionIn the adjoining figure BO and CO are the bisectors of ∠CBD and ∠BCE respectively. If AC>AB, prove that OB>OC.

View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionIn the adjoining figure, PS| |QR and ∠Q=115∘, then find the values of ∠P, anl≥R and ∠S.

View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:
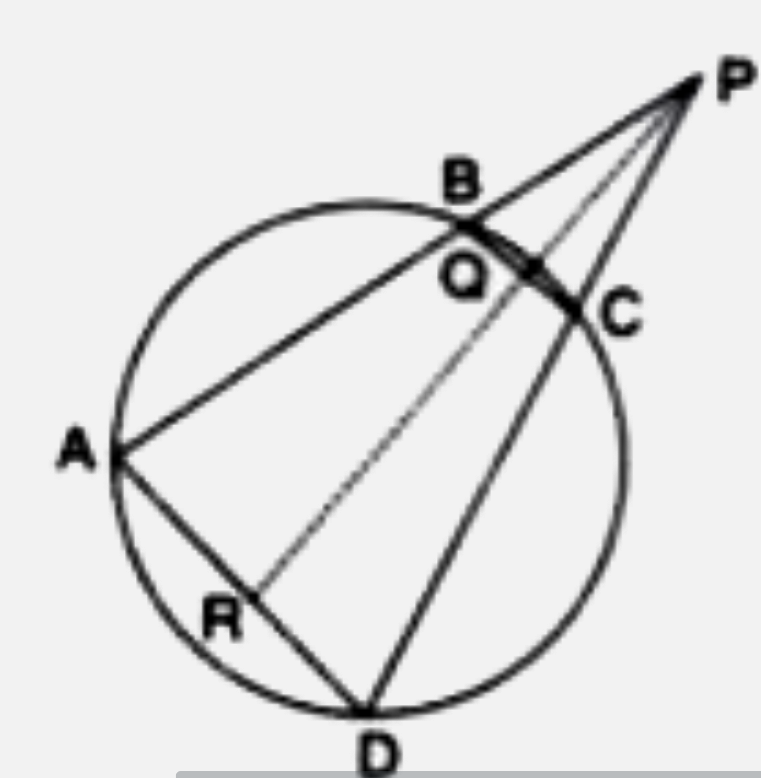
∠ARQ=∠BQR
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.

View Solution
