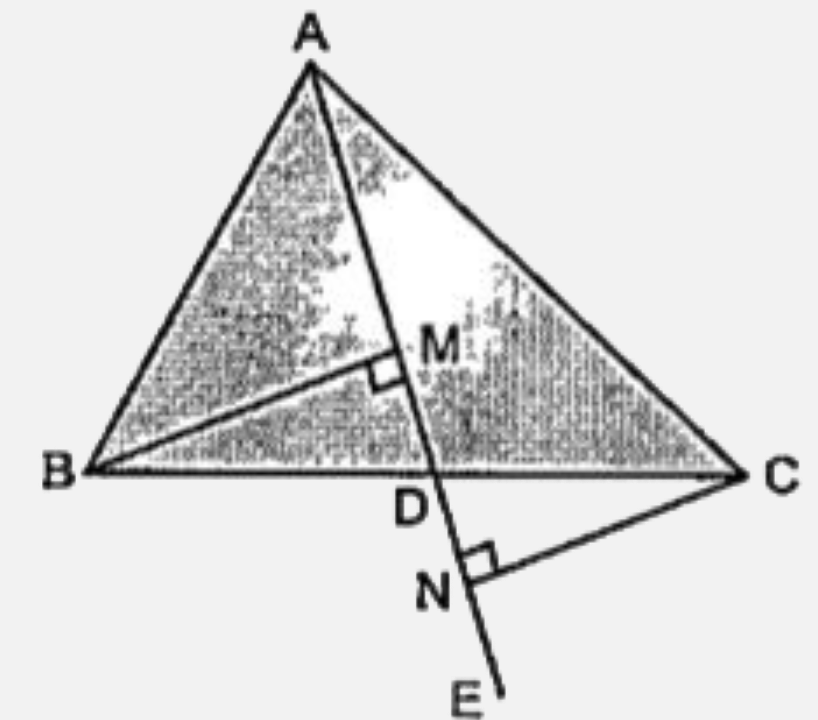
In the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that :
BM=CN
The correct Answer is:BM=CN
Step by step video & image solution for In the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE. Prove that : BM=CN by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that :
ΔBMD≅ΔCNDView SolutionIn the given figure ABC is a triangle and D is the mid-point of BC. AD is produced to E. BM and CN are two perpendiculars dropped from B and C respectively on AE.
Prove that : (i) ΔBMD≅ΔCND (ii) BM = CN
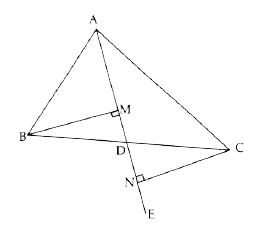
View SolutionIn the adjoining figure, D is the mid-point of BC. If BM and CN are perpendiculars from B and C respectively on AD and AD produced, then prove that BM = CN.
View SolutionIn the adjoining figure, BM and DN are the perpendiculars from B and D respectively to AC such that BM = DN. Prove that BO = OD.
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=ECView SolutionABC is a triangle. D is the middle point of BC. If AD is perpendicular to AC, The value of cos A cos C , is
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View Solution