A lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
To find the tension in the string of the lift, we can follow these steps:
Step 1: Identify the forces acting on the lift
The forces acting on the lift are:
- The tension (T) in the string acting upward.
- The weight of the lift (mg) acting downward, where m is the mass of the lift and g is the acceleration due to gravity.
Step 2: Write down the known values
- Mass of the lift (m) = 200 kg
- Acceleration due to gravity (g) = 10 m/s²
- Upward acceleration of the lift (a) = 3 m/s²
Step 3: Calculate the weight of the lift
The weight (W) of the lift can be calculated using the formula:
W=mg
Substituting the known values:
W=200kg×10m/s²=2000N
Step 4: Apply Newton's second law
According to Newton's second law, the net force acting on the lift can be expressed as:
T−mg=ma
Where:
- T is the tension in the string,
- mg is the weight of the lift,
- ma is the force due to the lift's acceleration.
Step 5: Rearrange the equation to solve for T
Rearranging the equation gives:
T=mg+ma
Step 6: Substitute the known values into the equation
Now substitute the values of m, g, and a into the equation:
T=(200kg×10m/s²)+(200kg×3m/s²)
T=2000N+600N
Step 7: Calculate the tension
Now, calculate the total tension:
T=2000N+600N=2600N
Final Answer:
The tension in the string of the lift is 2600 N.
---
The forces acting on the lift are:
- The tension (T) in the string acting upward.
- The weight of the lift (mg) acting downward, where m is the mass of the lift and g is the acceleration due to gravity.
- Mass of the lift (m) = 200 kg
- Acceleration due to gravity (g) = 10 m/s²
- Upward acceleration of the lift (a) = 3 m/s²
The weight (W) of the lift can be calculated using the formula:
W=mg
Substituting the known values:
W=200kg×10m/s²=2000N
According to Newton's second law, the net force acting on the lift can be expressed as:
T−mg=ma
Where:
- T is the tension in the string,
- mg is the weight of the lift,
- ma is the force due to the lift's acceleration.
Rearranging the equation gives:
T=mg+ma
Now substitute the values of m, g, and a into the equation:
T=(200kg×10m/s²)+(200kg×3m/s²)
T=2000N+600N
Now, calculate the total tension:
T=2000N+600N=2600N
The tension in the string of the lift is 2600 N.
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 3BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-B
13 Videos
- SELF ASSESSMENT PAPER 3BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-C
9 Videos
- SELF ASSESSMENT PAPER 02BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-D (Answer the following )
6 Videos
- SELF ASSESSMENT PAPER 4BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 4EXERCISE - Section-D
6 Videos
Similar Questions
A lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionA person of mass 60kg is inside a lift of mass 940kg and presses the button on control panel. The lift starts moving upword with an acceleration 1.0m/s2 . If g=10m/s2 , the tension in the supporting cable is.
View SolutionA lift of mass 1000 kg which is moving with an acceleration of 1ms−2 in upward direction , then the tension developed in string which is connected to lift is ___________
View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
View SolutionA lift of mass 1000kg is moving with an acceleration of 1m/s2 in upward direction. Tension developed in the string, which is connected to the lift, is.
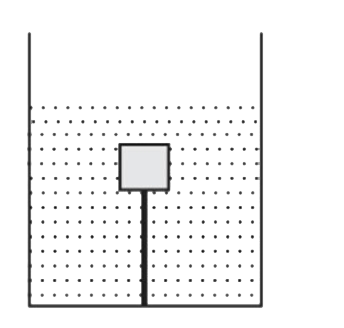
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionA man is standing on a weighing machine placed in a lift. When stationary his weight is recorded as 40 kg . If the lift is accelerated upwards with an acceleration of 2m/s2 , then the weight recorded in the machine will be (g=10m/s2)
View SolutionA rocket with a lift-off mass 3.5×104kg is blasted upwards with an initial acceleration of 10m/s2. Then the initial thrust of the blast is
View Solution
