A lift of mass is moving with an acceleration of in upward direction. Tension developed in the string, which is connected to the lift, is.
9800 N
10,800 N
11,000 N
10,000 N
The correct Answer is:2
To find the tension developed in the string connected to a lift moving upwards with an acceleration, we can follow these steps:
1. Identify the Given Values:
- Mass of the lift (m) = 1000 kg
- Acceleration of the lift (a) = 1 m/s²
- Acceleration due to gravity (g) = 10 m/s² (approximately)
2. Understand the Forces Acting on the Lift:
- The forces acting on the lift are:
- Weight of the lift (downward): W=m⋅g
- Tension in the string (upward): T
- Pseudo force (downward) due to the upward acceleration of the lift: Fpseudo=m⋅a
3. Calculate the Weight of the Lift:
W=m⋅g=1000kg⋅10m/s2=10000N
4. Calculate the Pseudo Force:
Fpseudo=m⋅a=1000kg⋅1m/s2=1000N
5. Apply Newton's Second Law:
When considering the forces acting on the lift, we can write the equation for tension:
T−W−Fpseudo=0
Rearranging gives:
T=W+Fpseudo
6. Substitute the Values:
T=10000N+1000N=11000N
7. Final Answer:
The tension developed in the string is T=11000N.
Conclusion:
The tension in the string connected to the lift is 11000 N.
---
- Mass of the lift (m) = 1000 kg
- Acceleration of the lift (a) = 1 m/s²
- Acceleration due to gravity (g) = 10 m/s² (approximately)
- The forces acting on the lift are:
- Weight of the lift (downward): W=m⋅g
- Tension in the string (upward): T
- Pseudo force (downward) due to the upward acceleration of the lift: Fpseudo=m⋅a
W=m⋅g=1000kg⋅10m/s2=10000N
Fpseudo=m⋅a=1000kg⋅1m/s2=1000N
When considering the forces acting on the lift, we can write the equation for tension:
T−W−Fpseudo=0
Rearranging gives:
T=W+Fpseudo
T=10000N+1000N=11000N
The tension developed in the string is T=11000N.
The tension in the string connected to the lift is 11000 N.
Topper's Solved these Questions
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:ENABLE
Explore 50 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:EFFICIENT
Explore 50 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:JEE Advanced (archive)
Explore 14 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
Similar Questions
A lift of mass 1000 kg which is moving with an acceleration of 1ms−2 in upward direction , then the tension developed in string which is connected to lift is ___________
View SolutionA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionA man weighing 60 kg is in a lift moving down with an acceleration of 1.8 ms−2. The force exerted by the floor on him is
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View Solution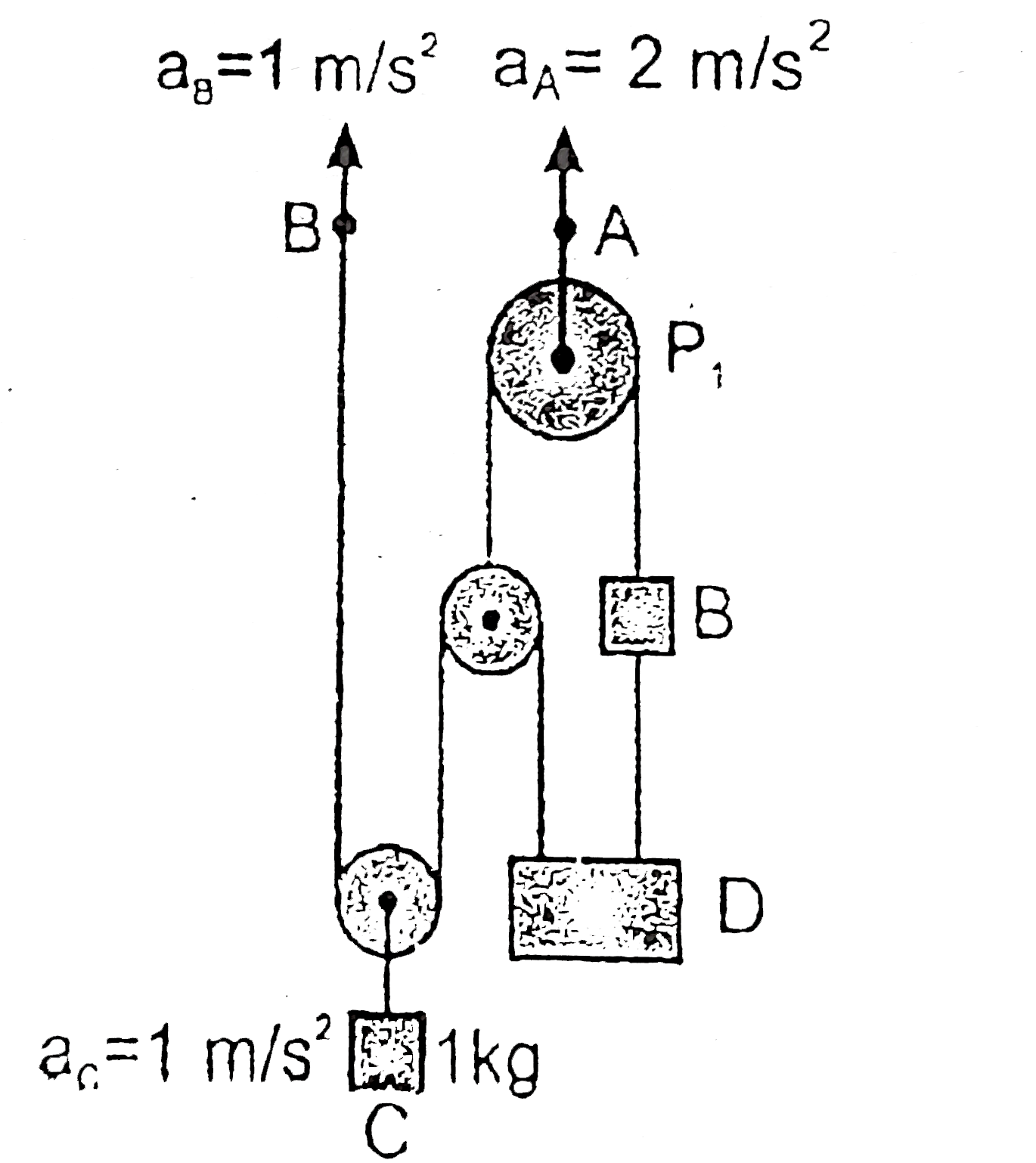
In the arrangement shown in figure pulley and strings are ideal. End A of string connected to pulley P1 is moved upwards with acceleration aA=2m/s2 while end B of another string shown in figure is moved up with acceleration aB=1m/s2. Block C of mass 1 kg is moving up with accelaration 1m/s2. If block D to which string are connected are connected symmetrically moves such that its orientations remains same then (assume g=10m/s2)
View SolutionA lift is moving in upward direction with speed 20m/s and having acceleration 5m/s2 in downward direction. A bolt drops from the ceiling of lift at that moment. Just after the drop, the:
View SolutionThe tension in the cord connected to motor is 15000 N and mass of the lift is 1400 kg. f mass m= 100 kg is inside the connected with a massless string as shown in tigure, then tension in the string connected with m is (g=10ms2)
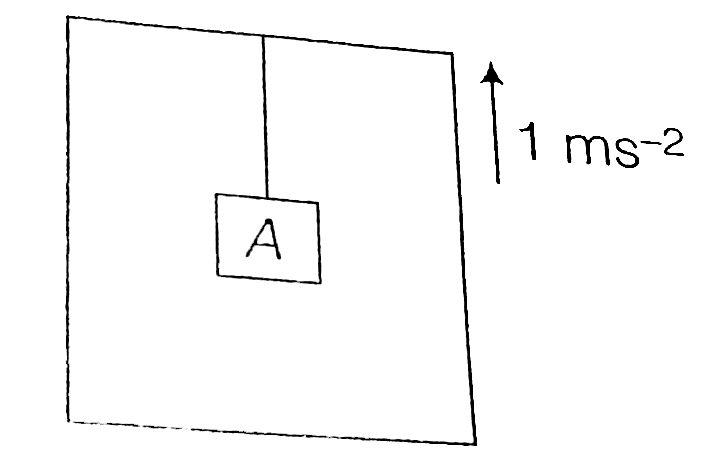
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
View Solution