(a) What is elastic potential energy of a spring ? Obtain the relation for elastic . Where k is force constant of spring, is extension or compression produced in the spring.
Step-by-Step Solution
Step 1: Definition of Elastic Potential Energy
- Elastic potential energy (EPE) is defined as the energy stored in a spring when it is either compressed or stretched from its natural (equilibrium) position.
Step 2: Setup the Problem
- Consider a spring with one end fixed to a rigid wall and the other end attached to a block on a frictionless surface. When we apply a force to the block, it moves from the natural length of the spring to a distance x (either compressed or elongated).
Step 3: Work Done Against the Spring Force
- When the spring is elongated by a small distance dr, the spring exerts a restoring force F=−kr (where k is the spring constant and r is the current extension or compression).
- The work done dW in moving the block by dr can be expressed as:
dW=F⋅dr=−krdr
Step 4: Total Work Done
- To find the total work done in moving the block from the natural length (where r=0) to the extension x, we integrate:
W=∫x0−krdr
Step 5: Perform the Integration
- The integral can be computed as follows:
W=−k∫x0rdr=−k(r22)x0=−k(x22−0)=−kx22
Step 6: Relate Work Done to Potential Energy
- The elastic potential energy U stored in the spring is equal to the negative of the work done by the spring force:
U=−W=kx22
Final Relation:
- Thus, the expression for the elastic potential energy of a spring is:
U=12kx2
- Elastic potential energy (EPE) is defined as the energy stored in a spring when it is either compressed or stretched from its natural (equilibrium) position.
- Consider a spring with one end fixed to a rigid wall and the other end attached to a block on a frictionless surface. When we apply a force to the block, it moves from the natural length of the spring to a distance x (either compressed or elongated).
- When the spring is elongated by a small distance dr, the spring exerts a restoring force F=−kr (where k is the spring constant and r is the current extension or compression).
- The work done dW in moving the block by dr can be expressed as:
dW=F⋅dr=−krdr
- To find the total work done in moving the block from the natural length (where r=0) to the extension x, we integrate:
W=∫x0−krdr
- The integral can be computed as follows:
W=−k∫x0rdr=−k(r22)x0=−k(x22−0)=−kx22
- The elastic potential energy U stored in the spring is equal to the negative of the work done by the spring force:
U=−W=kx22
- Thus, the expression for the elastic potential energy of a spring is:
U=12kx2
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 3BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-C
9 Videos
- SELF ASSESSMENT PAPER 02BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-D (Answer the following )
6 Videos
- SELF ASSESSMENT PAPER 4BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 4EXERCISE - Section-D
6 Videos
Similar Questions
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
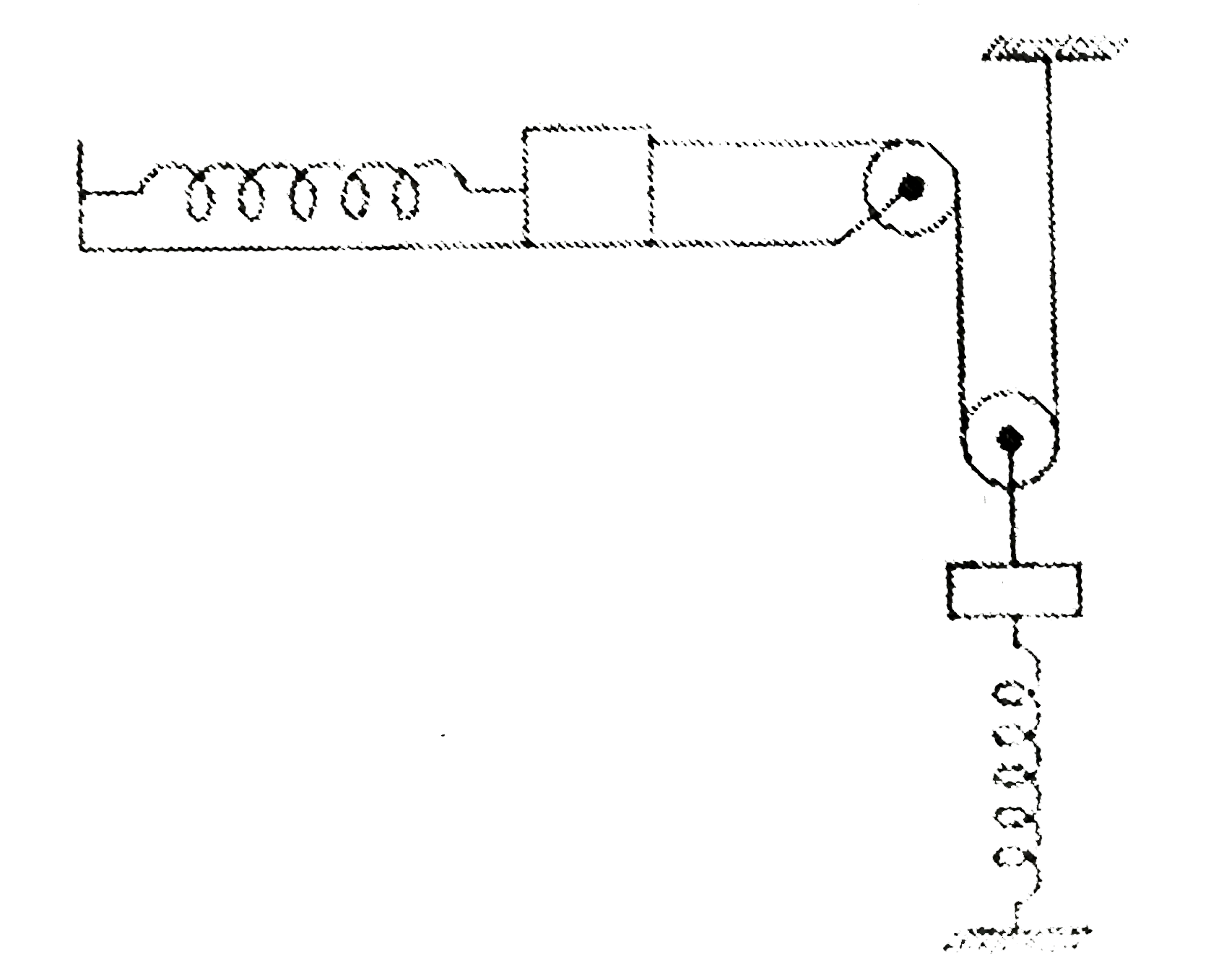
Extension of horizontal spring in equilibrium is
View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
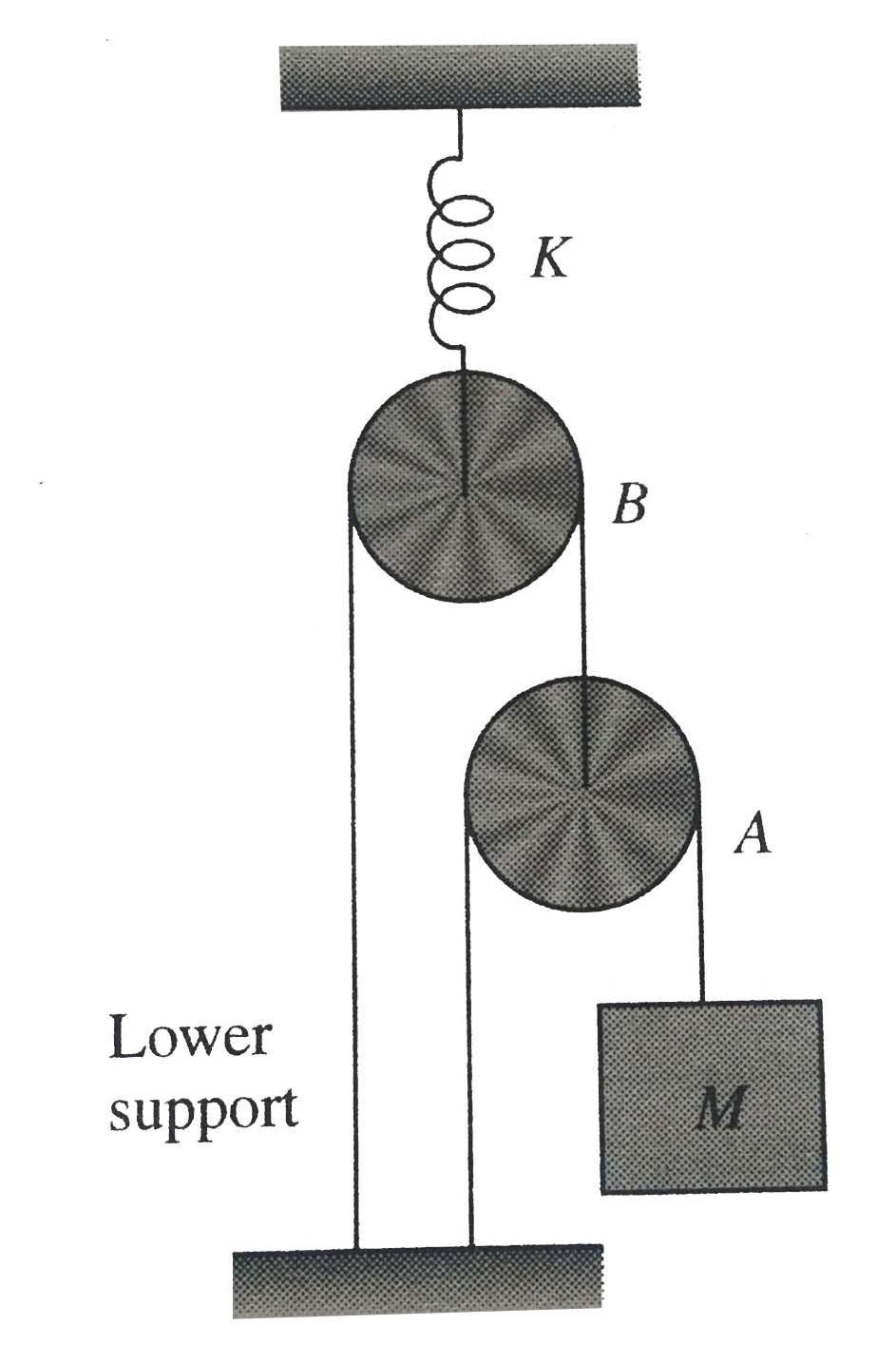
The extension produced in the spring is given by
View SolutionThe spring force is given by F=−kx, here k is a constant and x is the deformation of spring. The F−x graph is
View SolutionThe potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View SolutionAssuming that potential energy of spring is zero when it is stretched by x02, its potential energy when it is compressed by x0 is
View SolutionA solid cylinder of mass 3kg is rolling on a horizontal surface with velocity 4ms−1. It collides with a horizontal spring of force constant 200Nm−1. The maximum compression produced in the spring will be :
View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.

a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View Solution
