Three particles start from the origin at the same time, one with a velocity v1 along the x-axis, second along the y-axis with a velocity v2 and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
v1v2v1+v2
√2v1v2v1+v2
√3v1v2v1+v2
zero
The correct Answer is:B
To solve the problem, we need to find the velocity of the third particle moving along the line y=x such that all three particles remain collinear. Let's break down the solution step by step.
Step 1: Understand the Motion of Each Particle
- The first particle moves along the x-axis with a velocity v1. After time t, its position will be (v1t,0).
- The second particle moves along the y-axis with a velocity v2. After time t, its position will be (0,v2t).
- The third particle moves along the line y=x with an unknown velocity v3. After time t, its position will be (x,x).
Step 2: Find the Equation of the Line Connecting the First Two Particles
The line connecting the first two particles can be determined using the two points:
- Point A: (v1t,0)
- Point B: (0,v2t)
The slope m of the line connecting these two points is given by:
m=v2t−00−v1t=−v2v1
Using the point-slope form of the line equation, we can write the equation of the line as:
y−0=−v2v1(x−v1t)
Simplifying this, we get:
y=−v2v1x+v2t
Step 3: Find the Condition for Collinearity
For the third particle to be collinear with the first two particles, its position (x,x) must satisfy the line equation derived above. Therefore, substituting y=x into the line equation gives:
x=−v2v1x+v2t
Rearranging this equation:
x+v2v1x=v2t
x(1+v2v1)=v2t
x=v2t1+v2v1=v2v1tv1+v2
Step 4: Calculate the Distance R
The distance R traveled by the third particle in time t is given by:
R=√x2+x2=√2x2=x√2
Substituting the value of x:
R=v2v1tv1+v2√2
Step 5: Relate R to the Velocity of the Third Particle
The distance R can also be expressed in terms of the velocity v3 of the third particle:
R=v3t
Equating the two expressions for R:
v3t=v2v1t√2v1+v2
Dividing both sides by t (assuming t≠0):
v3=v2v1√2v1+v2
Final Answer
Thus, the velocity of the third particle is:
v3=√2v1v2v1+v2
- The first particle moves along the x-axis with a velocity v1. After time t, its position will be (v1t,0).
- The second particle moves along the y-axis with a velocity v2. After time t, its position will be (0,v2t).
- The third particle moves along the line y=x with an unknown velocity v3. After time t, its position will be (x,x).
The line connecting the first two particles can be determined using the two points:
- Point A: (v1t,0)
- Point B: (0,v2t)
m=v2t−00−v1t=−v2v1
y−0=−v2v1(x−v1t)
Simplifying this, we get:
y=−v2v1x+v2t
For the third particle to be collinear with the first two particles, its position (x,x) must satisfy the line equation derived above. Therefore, substituting y=x into the line equation gives:
x=−v2v1x+v2t
Rearranging this equation:
x+v2v1x=v2t
x(1+v2v1)=v2t
x=v2t1+v2v1=v2v1tv1+v2
The distance R traveled by the third particle in time t is given by:
R=√x2+x2=√2x2=x√2
Substituting the value of x:
R=v2v1tv1+v2√2
The distance R can also be expressed in terms of the velocity v3 of the third particle:
R=v3t
Equating the two expressions for R:
v3t=v2v1t√2v1+v2
Dividing both sides by t (assuming t≠0):
v3=v2v1√2v1+v2
Thus, the velocity of the third particle is:
v3=√2v1v2v1+v2
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)19videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 175videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)1videos
JEE MAIN REVISON TEST-23
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
Similar Questions
Three particles starts from origin at the same time with a velocity 2ms−1 along positive x-axis, the second with a velocity 6ms−1 along negative y-axis, Find the velocity of the third particle along x=y line so that the three particles may always lie in a straight line.
View SolutionAt any instant, the velocity and acceleration of a particle moving along a straight line are v and a. The speed of the particle is increasing if
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 View Solution
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
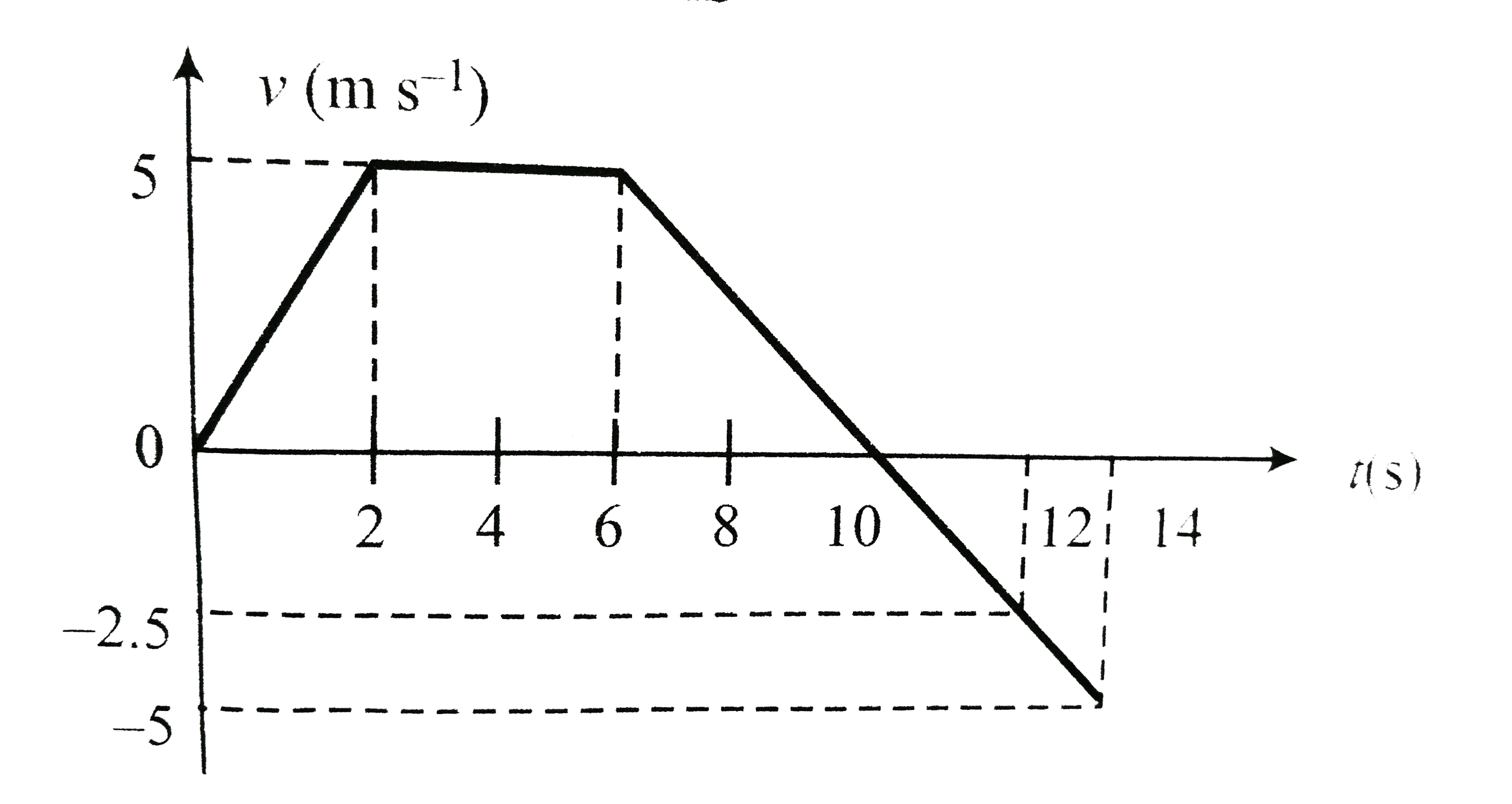 .View Solution
.View SolutionA particle starts from the origin, goes along the X-axis to the point (20m, 0) and then returns along the same line to the point (-20m,0). Find the distance and displacement of the particle during the trip.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
 View Solution
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View SolutionA particle is moving along x-axis. Its velocity v with x co-ordinate is varying as v=√x. Then
View Solution

