Calculate the amount of work done to dissociate a system of 3 charges 1μC,1μC and 4μC placed on the vertices of an equilateral triangle of sides 10 cm.
To calculate the amount of work done to dissociate a system of three charges 1μC, 1μC, and 4μC placed at the vertices of an equilateral triangle with side length 10 cm, we can follow these steps:
Step 1: Understand the Configuration
We have three charges:
- Charge QA=1μC=1×10−6C at vertex A
- Charge QB=1μC=1×10−6C at vertex B
- Charge QC=4μC=4×10−6C at vertex C
The distance between any two charges (the side of the triangle) is given as 10 cm, which is 0.1 m.
Step 2: Calculate the Potential Energy
The total potential energy U of the system of charges can be calculated using the formula for the potential energy between point charges:
U=k(QAQBrAB+QBQCrBC+QAQCrAC)
Where:
- k=14πϵ0≈9×109Nm2/C2
- rAB=rBC=rAC=0.1m
Step 3: Substitute the Values
Substituting the values into the potential energy formula:
U=k((1×10−6)(1×10−6)0.1+(1×10−6)(4×10−6)0.1+(1×10−6)(4×10−6)0.1)
Step 4: Simplify Each Term
Calculating each term:
1. For QAQB:
(1×10−6)(1×10−6)0.1=1×10−120.1=1×10−11
2. For QBQC:
(1×10−6)(4×10−6)0.1=4×10−120.1=4×10−11
3. For QAQC:
(1×10−6)(4×10−6)0.1=4×10−120.1=4×10−11
Step 5: Combine the Terms
Now, combine all the terms:
U=k(1×10−11+4×10−11+4×10−11)=k(9×10−11)
Step 6: Substitute k and Calculate U
Substituting k:
U=9×109×9×10−11=81×10−2=0.81J
Final Answer
The amount of work done to dissociate the system of charges is 0.81J.
---
We have three charges:
- Charge QA=1μC=1×10−6C at vertex A
- Charge QB=1μC=1×10−6C at vertex B
- Charge QC=4μC=4×10−6C at vertex C
The total potential energy U of the system of charges can be calculated using the formula for the potential energy between point charges:
- k=14πϵ0≈9×109Nm2/C2
- rAB=rBC=rAC=0.1m
Substituting the values into the potential energy formula:
Calculating each term:
(1×10−6)(1×10−6)0.1=1×10−120.1=1×10−11
(1×10−6)(4×10−6)0.1=4×10−120.1=4×10−11
(1×10−6)(4×10−6)0.1=4×10−120.1=4×10−11
Now, combine all the terms:
Substituting k:
The amount of work done to dissociate the system of charges is 0.81J.
Similar Questions
Calculate the amount of work done to dissociate a system of three charges 1μC,1μCand−4μC placed on vertices of an equilateral triangle of side 10 cm.
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View SolutionThree charges 2 μC , -4 μC and 8 μC are places at the three vertices of an equilateral triangle of side 10 cm. The potential at the centre of triangle is
View Solution(a) Derive an expression for the torque experienced by an electric dipole kept in a uniform electric field.
(b) Calculate the work done to dissociate the system of three charges placed on the vertices of a triangle as shown.
Here q=1.6×10−10C.

View SolutionElectric charge of 1μC,−1μC and 2μC are placed in air at the corners A, B and C respectively of an equilateral triangle ABC having length of each side 10 cm. The resultant force on the charge at C is
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
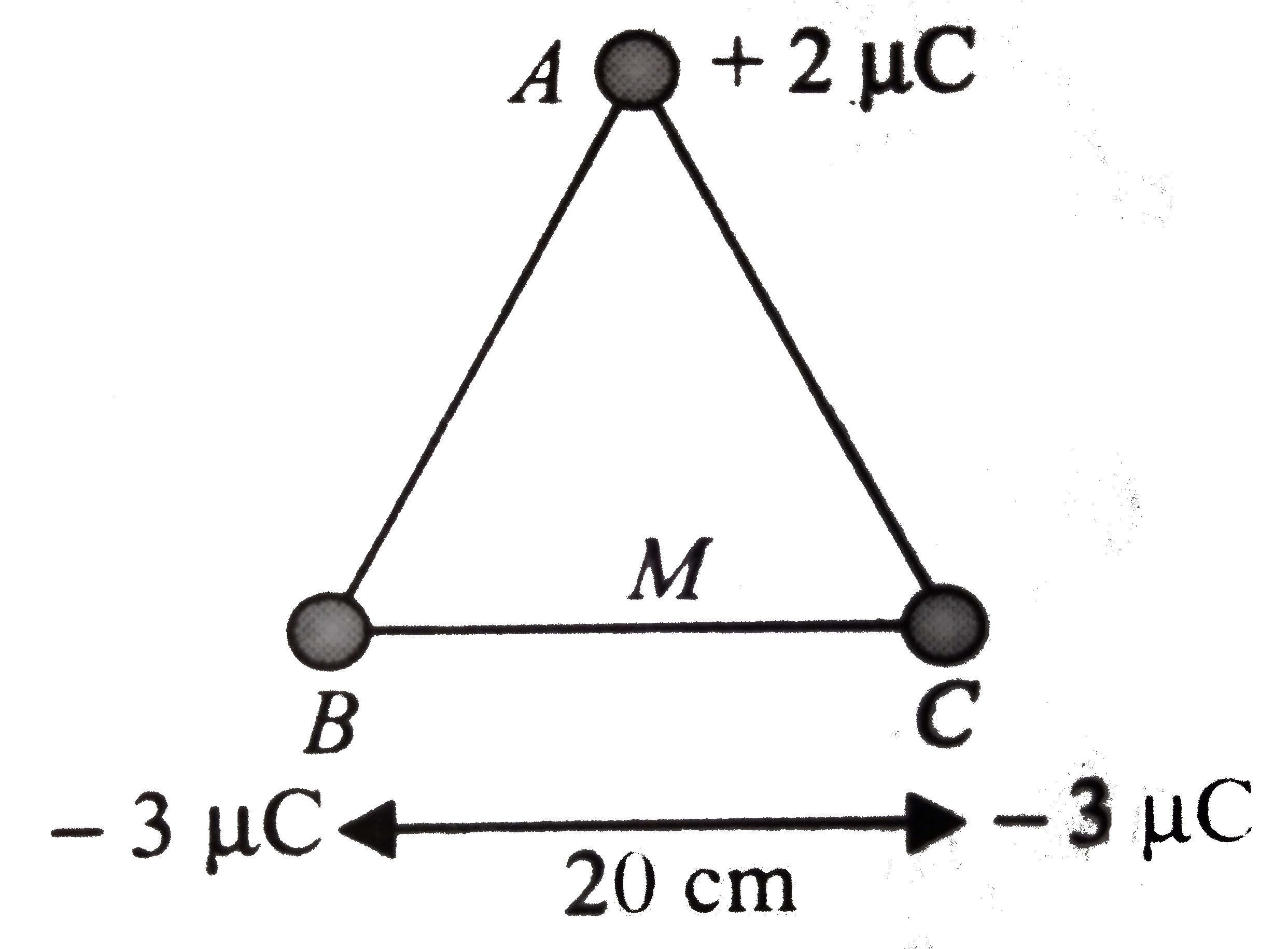
View SolutionThree point charges of +2μC,−3μC , and −3μC are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
View SolutionThree identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
View SolutionFour point charges 1μC,3μC,−2μCand−2μC are arranged on the four vertices of a square of side 1 cm. The dipole moment of this charge assembly is

View Solution
