A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
straight line
arc of circle
parabola
ellipse
The correct Answer is:c
To solve the problem of determining the path of a particle moving in a plane with constant acceleration in a direction different from its initial velocity, we can follow these steps:
1. Identify the Variables:
- Let the initial velocity of the particle be →v.
- Let the constant acceleration be →a.
- Let the angle between the initial velocity and acceleration be θ.
2. Break Down the Velocity and Acceleration:
- The initial velocity can be broken down into two components:
- vx=vcosθ (horizontal component)
- vy=vsinθ (vertical component)
3. Apply Kinematic Equations:
- The vertical motion can be described by the equation:
y=vyt+12ayt2
- Here, ay is the vertical component of acceleration. Since the acceleration is constant and directed differently, we can assume ay=a.
4. Substituting the Components:
- Substitute vy and ay into the equation:
y=(vsinθ)t+12at2
5. Horizontal Motion:
- The horizontal motion is given by:
x=vxt
- Substitute vx:
x=(vcosθ)t
- From this, we can express time t in terms of x:
t=xvcosθ
6. Substituting Time into the Vertical Equation:
- Substitute t back into the vertical motion equation:
y=(vsinθ)(xvcosθ)+12a(xvcosθ)2
- Simplifying this gives:
y=xtanθ+12ax2v2cos2θ
7. Identifying the Path:
- The equation derived is of the form:
y=Ax+Bx2
- This is a quadratic equation in x, which represents a parabola.
Conclusion:
The path of the particle is a parabola.
- Let the initial velocity of the particle be →v.
- Let the constant acceleration be →a.
- Let the angle between the initial velocity and acceleration be θ.
- The initial velocity can be broken down into two components:
- vx=vcosθ (horizontal component)
- vy=vsinθ (vertical component)
- The vertical motion can be described by the equation:
y=vyt+12ayt2
- Here, ay is the vertical component of acceleration. Since the acceleration is constant and directed differently, we can assume ay=a.
- Substitute vy and ay into the equation:
y=(vsinθ)t+12at2
- The horizontal motion is given by:
x=vxt
- Substitute vx:
x=(vcosθ)t
- From this, we can express time t in terms of x:
t=xvcosθ
- Substitute t back into the vertical motion equation:
y=(vsinθ)(xvcosθ)+12a(xvcosθ)2
- Simplifying this gives:
y=xtanθ+12ax2v2cos2θ
- The equation derived is of the form:
y=Ax+Bx2
- This is a quadratic equation in x, which represents a parabola.
The path of the particle is a parabola.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( Laws of motion )
36 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( WORK POWER ENERGY )
35 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics (UNIFORMLY ACCELERATED MOTION)
58 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
A particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
View SolutionA particle moves in the plane xy with constant acceleration 'a' directed along the negative y-axis. The equation of motion of the particle has the form y=px−qx2 where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
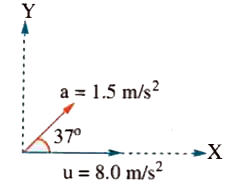
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionStarting from origin at t=0, with initial velocity 5ˆjm/s, a particle moves in the x−y plane with a constant acceleration of (10ˆi−5ˆj)m/s2. Find the coordinates of the particle at the moment its y-coordinate is maximum.
View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
View Solution
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive
View SolutionA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA particle starts from the origin of coordinates at time t = 0 and moves in the xy plane with a constant acceleration α in the y-direction. Its equation of motion is y=βx2. Its velocity component in the x-direction is
View Solution