Starting from rest, a body slides down a 45∘ inclined plane in twice the time it itakes to slide the same distance in the absence of friction.
They the coefficient of friction between the body and the inclined plane is
1/4
2/3
3/4
√3/2
The correct Answer is:c
To solve the problem step by step, we will analyze the motion of the body on the inclined plane both with and without friction.
Step 1: Understanding the Problem
The body starts from rest and slides down a 45∘ inclined plane. It takes time t to slide down the incline with friction and t/2 to slide down the same distance without friction.
Step 2: Setting Up the Equations
1. Without Friction:
- The acceleration a of the body down the incline without friction is given by:
a=gsinθ=gsin45∘=g√2
- Using the equation of motion:
s=ut+12at2
- Since the body starts from rest (u=0):
s=12(g√2)(t2)2=12(g√2)(t24)=gt28√2
2. With Friction:
- The acceleration a′ of the body down the incline with friction is:
a′=gsinθ−f=gsin45∘−μgcos45∘=g√2−μg√2=g(1−μ)√2
- Using the same equation of motion:
s=12a′t2=12(g(1−μ)√2)t2
Step 3: Equating the Distances
Since the distance s is the same in both cases, we can set the two equations equal to each other:
gt28√2=12(g(1−μ)√2)t2
Step 4: Simplifying the Equation
1. Cancel g and t2 from both sides (assuming g and t are not zero):
18√2=1−μ2√2
2. Multiply both sides by 2√2:
28=1−μ
14=1−μ
3. Rearranging gives:
μ=1−14=34
Step 5: Conclusion
The coefficient of friction μ between the body and the inclined plane is:
μ=34
Final Answer
The correct option is 34.
---
The body starts from rest and slides down a 45∘ inclined plane. It takes time t to slide down the incline with friction and t/2 to slide down the same distance without friction.
1. Without Friction:
- The acceleration a of the body down the incline without friction is given by:
a=gsinθ=gsin45∘=g√2
- Using the equation of motion:
s=ut+12at2
- Since the body starts from rest (u=0):
s=12(g√2)(t2)2=12(g√2)(t24)=gt28√2
- The acceleration a′ of the body down the incline with friction is:
a′=gsinθ−f=gsin45∘−μgcos45∘=g√2−μg√2=g(1−μ)√2
- Using the same equation of motion:
s=12a′t2=12(g(1−μ)√2)t2
Since the distance s is the same in both cases, we can set the two equations equal to each other:
gt28√2=12(g(1−μ)√2)t2
1. Cancel g and t2 from both sides (assuming g and t are not zero):
18√2=1−μ2√2
2. Multiply both sides by 2√2:
28=1−μ
14=1−μ
3. Rearranging gives:
μ=1−14=34
The coefficient of friction μ between the body and the inclined plane is:
μ=34
The correct option is 34.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - MOTION IN FLUIDS25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - UNIFORM CIRCULAR MOTION25videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - Dynamics ( WORK POWER ENERGY )35videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
Similar Questions
Starting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionStarting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View Solution
Knowledge Check
- Question 1 - Select One
When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time 20s. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it takes time 20p is, where p is some number greater than 1. The coefficient of friction between the body and the rough plane is
Aμ=(1−1p2)1√3Bμ=(1−19p2)Cμ=(1−p2)1√3Dμ=√1−9p2
A piece of ice slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View SolutionThe time taken by a body to slide down a rough 45∘ inclined plane is twice that required to slide down a smooth 45∘ inclined plane. The coefficient of kinetic friction between the object and rough plane is given by
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
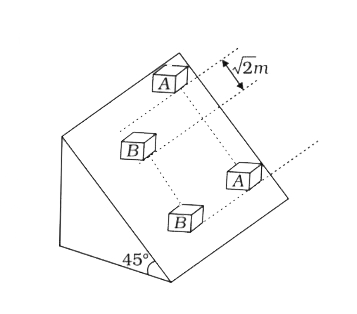 View Solution
View SolutionA body is pushed up on a rough inclined plane making an angle 30∘ to the horizontal. If its time of ascent on the plane is half the time of its descent, find coefficient of friction between the body and the incined plane.
View SolutionIf the angle of inclination of the inclined plane is sin−1(12) when the body just starts sliding find the angle of repose and coefficient of static friction between the body and the inclined plane.
View SolutionThe minimum force required to move a body up an inclined plane is three times the minimum force required to prevent it from sliding down the plane. If the coefficient of friction between the body and the inclined plane is 12√3, the angle of the inclined plane is
View SolutionA given object taken n time more time to slide down 45∘ rough inclined plane as it taken to slide down a perfectly smooth 45∘ incline The coefficient of kintic friction between the object and the incline is .
View Solution

