Calculate the I−I distance in (Å) for given compound H2C2I2 if C−I bond length is 2.35Å. (sin60∘=0.866)
The correct Answer is:4
To calculate the I-I distance in the compound H₂C₂I₂, we will follow these steps:
Step 1: Understand the Structure of H₂C₂I₂
The compound H₂C₂I₂ has a structure where two carbon atoms are double-bonded to each other (C=C), and each carbon is bonded to one iodine atom (I). The structure can be represented as:
HH C=CII
Step 2: Determine the Hybridization of Carbon
Each carbon atom in H₂C₂I₂ is bonded to two other atoms (one carbon and one iodine). The steric number for each carbon is calculated as follows:
- Number of sigma bonds = 2 (one C-C bond and one C-I bond)
- Number of lone pairs = 0
Thus, the steric number is 2, indicating that each carbon is sp² hybridized.
Step 3: Identify the Bond Angles
In an sp² hybridized molecule, the bond angles are approximately 120 degrees. This means that the angle between the two C-I bonds is 120 degrees.
Step 4: Analyze the Geometry
To find the I-I distance, we can visualize the geometry. The angle between the two C-I bonds is 120 degrees. If we bisect this angle, we can find the angle between the line connecting the two iodine atoms and the line connecting the carbon atoms.
Step 5: Use the Sine Rule
We can denote:
- O as the midpoint between the two iodine atoms.
- I as the position of one iodine atom.
- C as the position of one carbon atom.
From the geometry, we can see that:
- The angle ICO = 60 degrees (half of 120 degrees).
- The angle IOC = 90 degrees.
Using the sine function:
\(
\sin(60^\circ) = \frac{IO}{CI}
\)
Where:
- \( IO \) is the distance from the iodine atom to the midpoint O.
- \( CI \) is the bond length of C-I, which is given as 2.35 Å.
Step 6: Solve for IO
Rearranging the sine equation gives:
\(
IO = CI \cdot \sin(60^\circ)
\)
Substituting the values:
\(
IO = 2.35 \, \text{Å} \times 0.866
\)
Calculating this gives:
\(
IO \approx 2.0351 \, \text{Å}
\)
Step 7: Calculate the I-I Distance
The I-I distance (II) is twice the distance from one iodine atom to the midpoint O:
\(
II = 2 \times IO
\)
Substituting the value of IO:
\(
II = 2 \times 2.0351 \, \text{Å} \approx 4.0702 \, \text{Å}
\)
Rounding this gives:
\(
II \approx 4 \, \text{Å}
\)
Final Answer
The I-I distance in the compound H₂C₂I₂ is approximately 4 Å.
---
The compound H₂C₂I₂ has a structure where two carbon atoms are double-bonded to each other (C=C), and each carbon is bonded to one iodine atom (I). The structure can be represented as:
HH C=CII
Each carbon atom in H₂C₂I₂ is bonded to two other atoms (one carbon and one iodine). The steric number for each carbon is calculated as follows:
- Number of sigma bonds = 2 (one C-C bond and one C-I bond)
- Number of lone pairs = 0
In an sp² hybridized molecule, the bond angles are approximately 120 degrees. This means that the angle between the two C-I bonds is 120 degrees.
To find the I-I distance, we can visualize the geometry. The angle between the two C-I bonds is 120 degrees. If we bisect this angle, we can find the angle between the line connecting the two iodine atoms and the line connecting the carbon atoms.
We can denote:
- O as the midpoint between the two iodine atoms.
- I as the position of one iodine atom.
- C as the position of one carbon atom.
- The angle ICO = 60 degrees (half of 120 degrees).
- The angle IOC = 90 degrees.
\(
\sin(60^\circ) = \frac{IO}{CI}
\)
Where:
- \( IO \) is the distance from the iodine atom to the midpoint O.
- \( CI \) is the bond length of C-I, which is given as 2.35 Å.
Rearranging the sine equation gives:
\(
IO = CI \cdot \sin(60^\circ)
\)
Substituting the values:
\(
IO = 2.35 \, \text{Å} \times 0.866
\)
Calculating this gives:
\(
IO \approx 2.0351 \, \text{Å}
\)
The I-I distance (II) is twice the distance from one iodine atom to the midpoint O:
\(
II = 2 \times IO
\)
Substituting the value of IO:
\(
II = 2 \times 2.0351 \, \text{Å} \approx 4.0702 \, \text{Å}
\)
Rounding this gives:
\(
II \approx 4 \, \text{Å}
\)
The I-I distance in the compound H₂C₂I₂ is approximately 4 Å.
Topper's Solved these Questions
Similar Questions
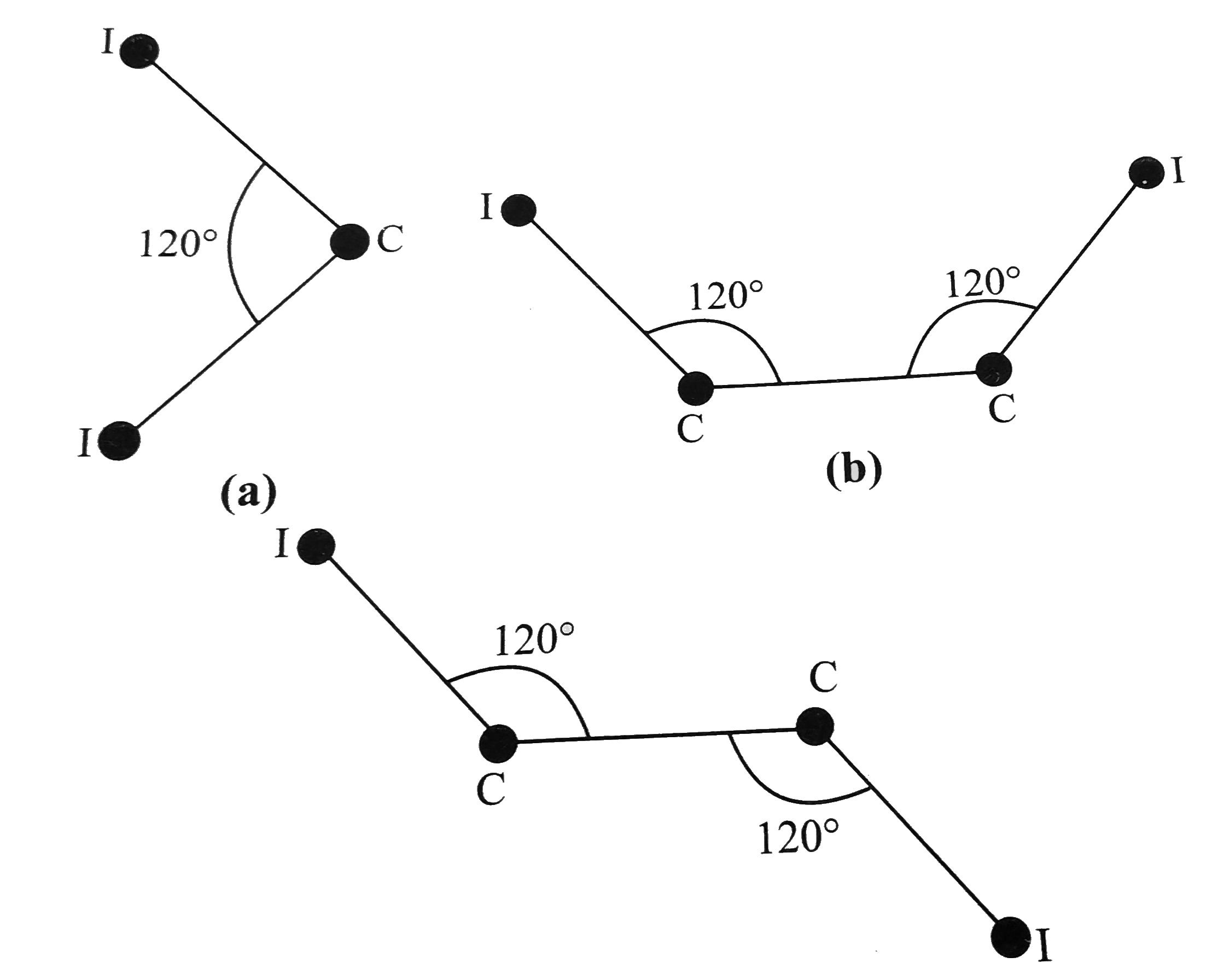
Calculate the I-I distance in each of the isomeric compounds C2H2I2 as shown below
Give Bond length of C−I⇒210 pm
Bond length of C=C⇒133 pm

 .View Solution
.View SolutionCalculate the DU of following compounds :
(i) C6H6ClBrO , (ii) C5H9NView SolutionThe bond length in H2 molecule is 0.174 Å.
View SolutionWrite the I.U.P.A.C. names of the following compounds:
C2H5−O−C2H5View SolutionConsider the statement ltbrlt I. Bond length in N+2 is 0.02Å greater than in N2.
II. Bond length of NO+ is 0.09Å less than in NO.
III O2−2 has shorter bond length than O2.
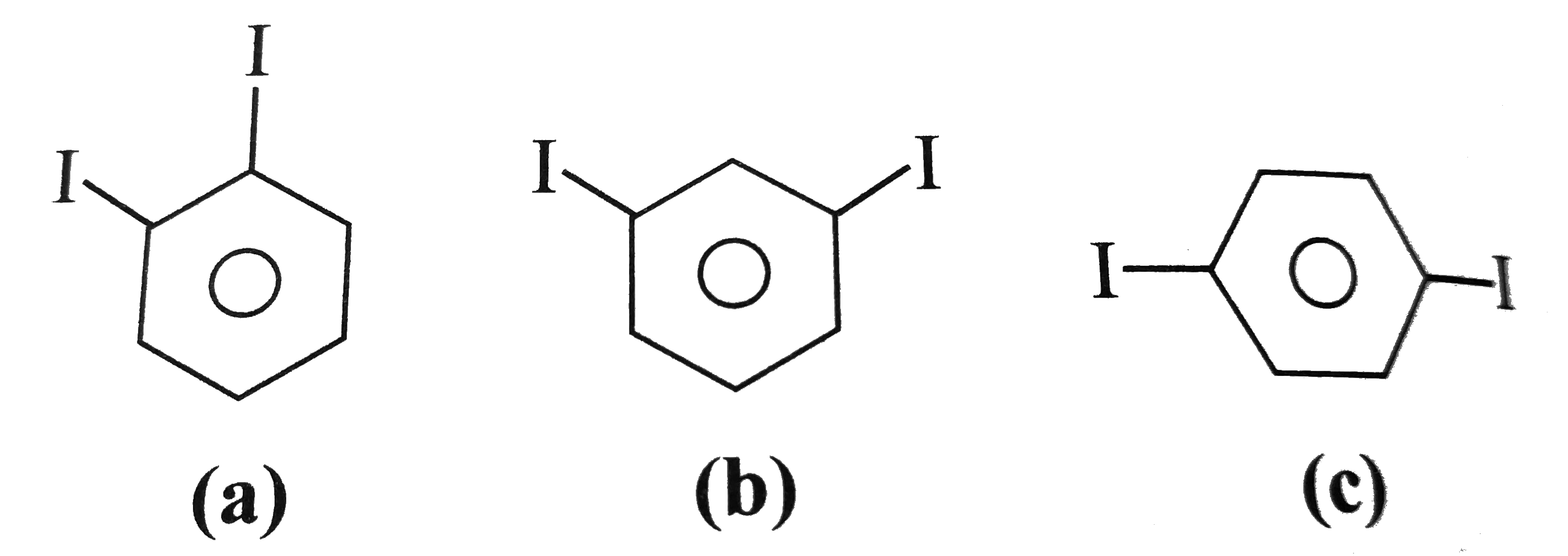
Which of the following statements are true?View SolutionCalculate the I-I distance in each of the three isomeric diiodobenzenes Assume that the ring is a regular hexagon and that each C−I bonds lies on a line through the centre of the hexagon .
Given C−I bond length =210 pm
The distance between two adjacent C-atom (i.e C-C)
=140 pm
 .View Solution
.View SolutionFor the given network calculate current I and I2.
 View Solution
View SolutionThe dipole moment of compound AB is 10.92 D and that of compound CD is 12.45 D. The bond length AB is 2.72 Å and that of CD is 2.56 Å then for these compound true statement is
View SolutionOne mole of H2 two moles of I2 and three moles of HI are injected in one litre flask. What will be the concentration of H2,I2 and HI at equilibrium at 500∘C.Kc for reaction H2+I2⇔2HI is 45.9.
View SolutionComment on the C-C bond length for C2H6 and C2F6 compounds
View Solution

