A force F=−k(yˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
For motion of the particle from (0,0)to(a,0),
→F=−K(0ˆi+aˆj)⇒→F=−Kaj
Displacement, →r=(aˆi+0ˆj)−(0ˆi+0ˆj)=aˆi
so work done from (0,0)to(a,0) is given by
W=→F.→r=−Kaˆj.aˆi=0
For motion (a,0) to (a,a)
→F=−K(aˆi+ˆj)
and displacement, →r=(aˆi+aˆj)−(aˆi+0ˆj)=aˆj
So work done from (a,0) to(a,a)
W=→F.→r=−K(aˆi+aˆj).aˆj=−Ka2
So total work done =−Ka2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Subjective28videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Single Correct51videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.119videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
Similar Questions
A force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View Solution
Knowledge Check
- Question 1 - Select One
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
A563 JB560 JC5603 JD3560 J
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
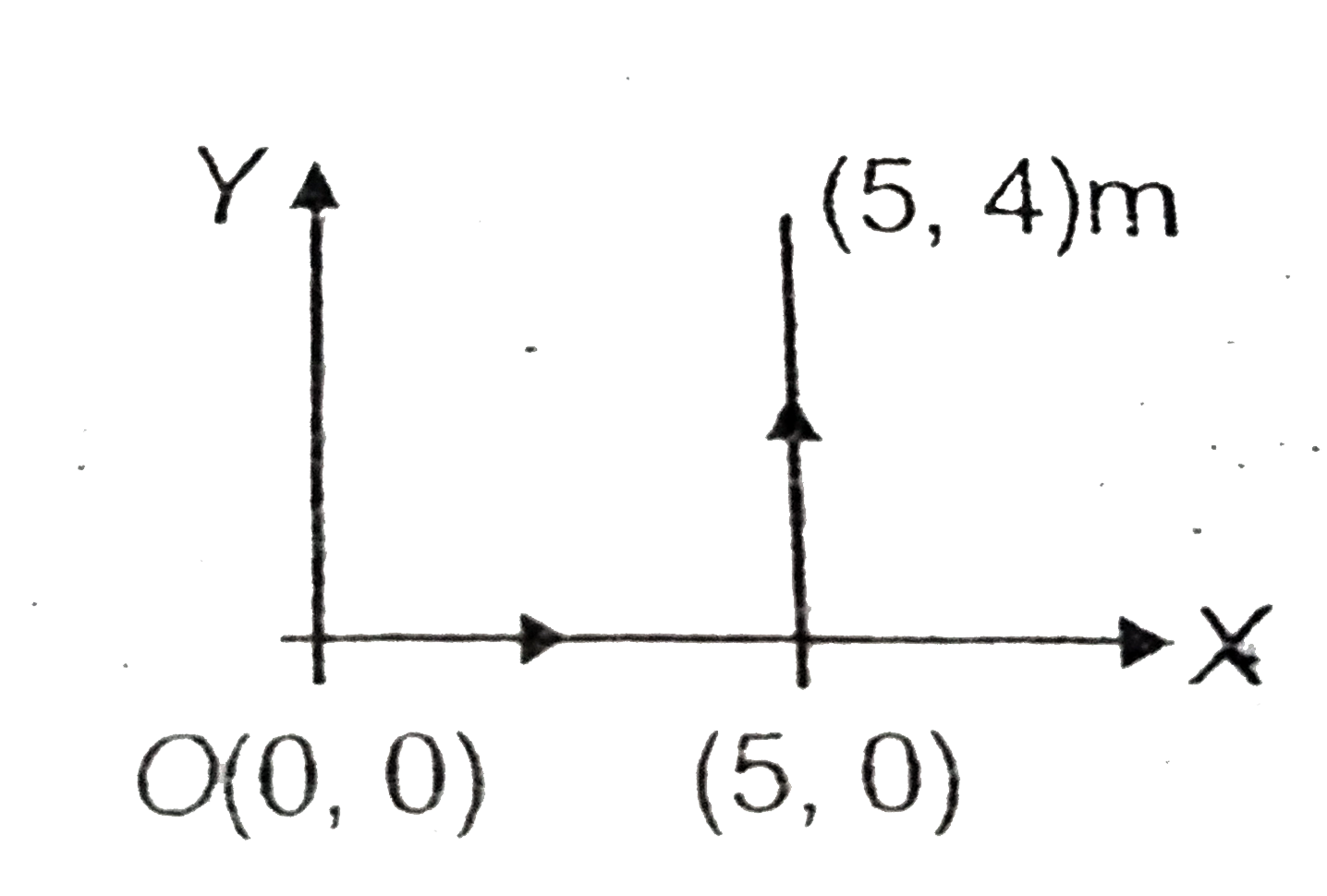 View Solution
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA particle moves in the x−y plane , accoding to the equation, r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View SolutionA uniform force of (3ˆi+ˆj) N acts on a particle of mass 2kg. Hence, the particle is displaced from position (2ˆi+ˆk)m to position (4ˆi+3ˆj−ˆk)m. The work done by the force on the particle is
View SolutionA particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
View SolutionThree components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
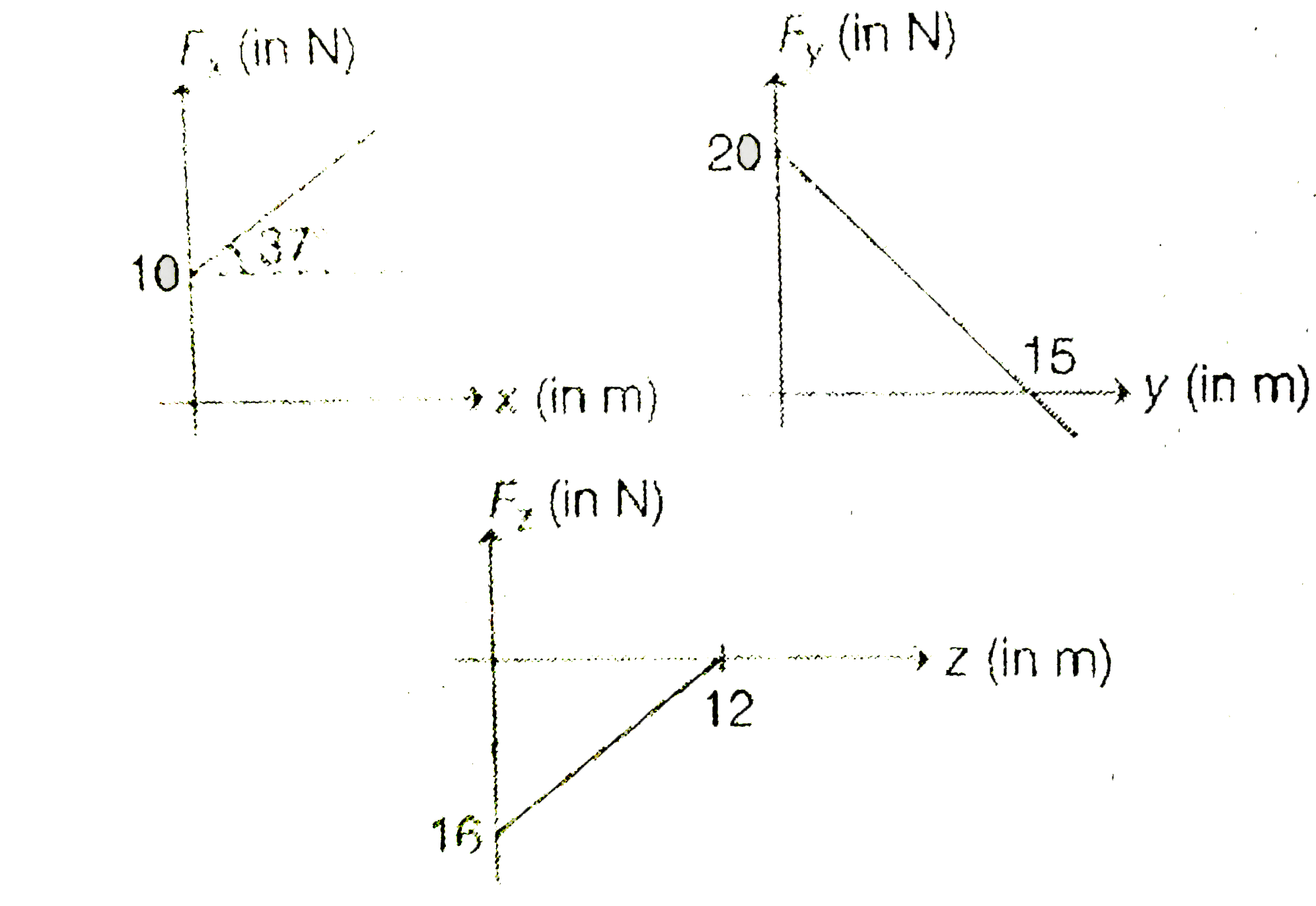 View Solution
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View Solution

