In an equilateral triangle ABC, AL, BM, and CN are medians. Forces along BC and BA represented by them will have a resultant represented by
2AL
2BM
2CN
AC
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Draw the Equilateral Triangle
We start by drawing an equilateral triangle ABC. In this triangle, all sides are equal, and we denote the vertices as follows:
- A is at the top vertex,
- B is the bottom left vertex,
- C is the bottom right vertex.
Step 2: Identify the Medians
The medians of the triangle are:
- AL: the median from vertex A to the midpoint L of side BC,
- BM: the median from vertex B to the midpoint M of side AC,
- CN: the median from vertex C to the midpoint N of side AB.
Step 3: Determine the Angles
In an equilateral triangle, each angle measures 60 degrees. When we consider the triangle formed by the median BM and the sides BC and BA, we can see that:
- The angle at vertex B (∠ABC) is 60 degrees.
- The angles at points L and M are 30 degrees each, since the median divides the triangle into two 30-60-90 triangles.
Step 4: Calculate the Length of the Median
Using the properties of a 30-60-90 triangle, we can find the length of the median BM. The formula for the length of a median in an equilateral triangle is:
BM=√32⋅a
where a is the length of each side of the triangle.
Step 5: Find the Resultant of Forces
The forces along BC and BA can be represented as vectors. Since BC and BA are equal in magnitude (both equal to a), we can find the resultant of these two forces using the cosine law:
R=√BC2+BA2+2⋅BC⋅BA⋅cos(60∘)
Substituting BC=BA=a and cos(60∘)=12:
R=√a2+a2+2⋅a2⋅12
R=√2a2+a2=√3a2=a√3
Step 6: Relate the Resultant to the Median
Since we have already calculated that the length of the median BM is √32a, we can express the resultant in terms of the median:
R=2⋅BM
Thus, the resultant of the forces along BC and BA is equal to twice the length of the median BM.
Conclusion
The resultant of the forces along BC and BA is represented by:
R=2⋅BM
We start by drawing an equilateral triangle ABC. In this triangle, all sides are equal, and we denote the vertices as follows:
- A is at the top vertex,
- B is the bottom left vertex,
- C is the bottom right vertex.
The medians of the triangle are:
- AL: the median from vertex A to the midpoint L of side BC,
- BM: the median from vertex B to the midpoint M of side AC,
- CN: the median from vertex C to the midpoint N of side AB.
In an equilateral triangle, each angle measures 60 degrees. When we consider the triangle formed by the median BM and the sides BC and BA, we can see that:
- The angle at vertex B (∠ABC) is 60 degrees.
- The angles at points L and M are 30 degrees each, since the median divides the triangle into two 30-60-90 triangles.
Using the properties of a 30-60-90 triangle, we can find the length of the median BM. The formula for the length of a median in an equilateral triangle is:
BM=√32⋅a
where a is the length of each side of the triangle.
The forces along BC and BA can be represented as vectors. Since BC and BA are equal in magnitude (both equal to a), we can find the resultant of these two forces using the cosine law:
R=√BC2+BA2+2⋅BC⋅BA⋅cos(60∘)
Substituting BC=BA=a and cos(60∘)=12:
R=√a2+a2+2⋅a2⋅12
R=√2a2+a2=√3a2=a√3
Since we have already calculated that the length of the median BM is √32a, we can express the resultant in terms of the median:
R=2⋅BM
Thus, the resultant of the forces along BC and BA is equal to twice the length of the median BM.
The resultant of the forces along BC and BA is represented by:
R=2⋅BM
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Subjective28videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
Similar Questions
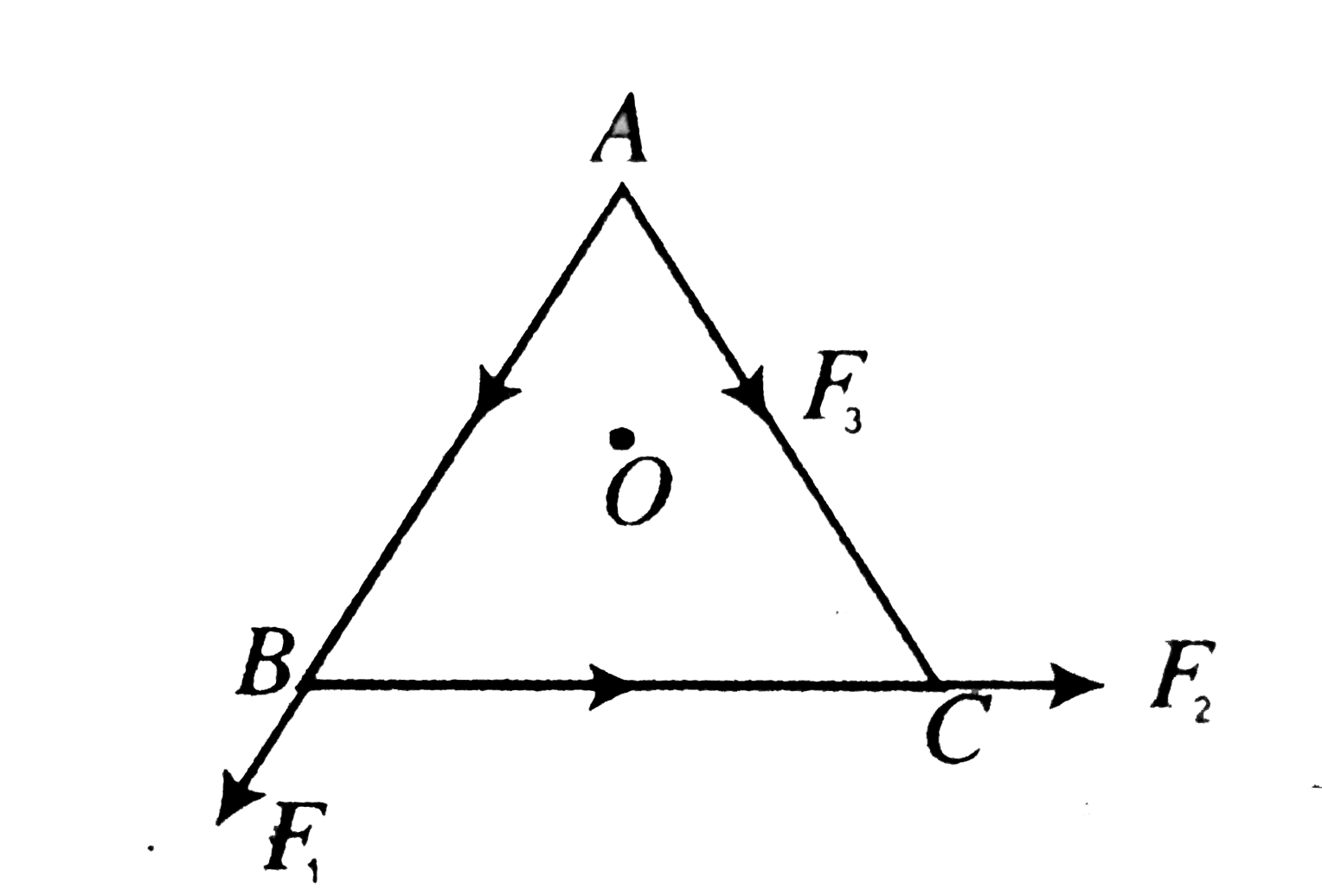
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
 View Solution
View SolutionConstruct an equilateral ΔABC in which BC=5cm.
View SolutionThree similar charges +q are placed on 3 corners of an equilateral triangle ABC of side a. How many minimum charges should be placed on a circle of radius a with centre at A so that resultant force on the charge placed at the centre is q24πε0a2 along x-axis,
 View Solution
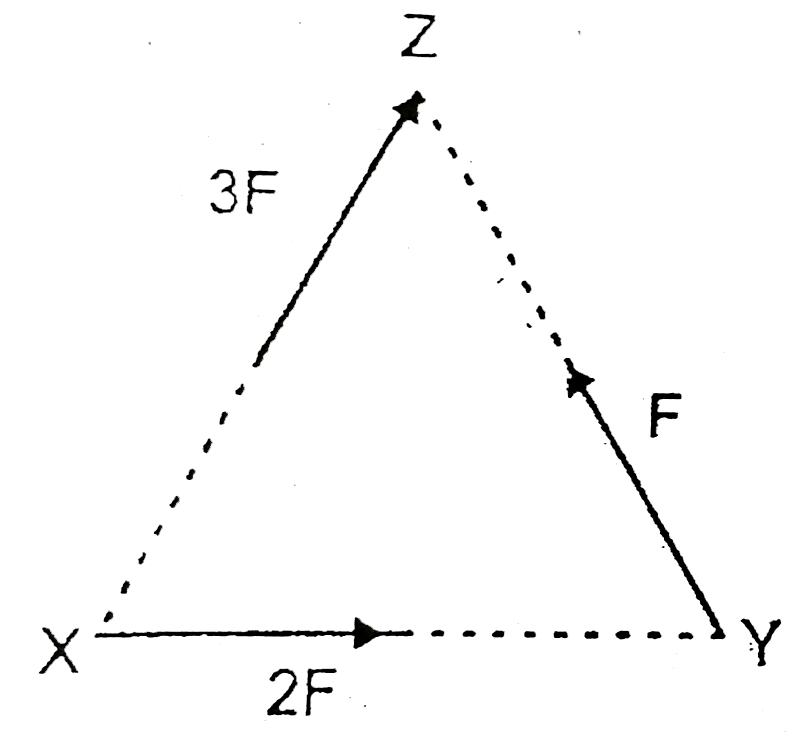
View SolutionIf XYZ is an equilateral triangle. Then the resultant of the three forces shown in the figure is :
 View Solution
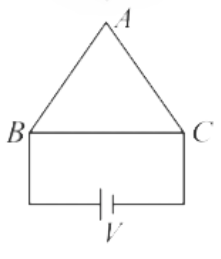
View SolutionAn equilateral triangle ABC of side length a is made. The sides AB and AC have resistance per unit length β, and side BC has resistasnce per unit length 2β. An ideal battery of EMF V is now connected across BC as shown. The magnetic field intensity at the centrroid of the triangle ABC is n(μ0V4πβ2), then the value of n is _______. (Consider only the field due to sides AB, BC and AC of the triangle, and neglect the field due to other wires)
 View Solution
View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is
 View Solution
View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is
 View Solution
View SolutionAn equilateral triangle ABC if formed by two Cu rods AB and BC and one Al rod

it is heated in such a way that temperature of each rod increases by ΔT. Find change in the angle ABC. [Coeff. Of linear expansion for Cu. is α1, Coeff. of linear expansion for Al is α2]View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionABC is an equilateral triangle. Taking BC as the base, construct a right angled triangle equal in area to equilateral triangle ABC.
View Solution

