Two point masses 1 and 2 move with uniform velocities →v1 and →v2, respectively. Their initial position vectors are →r1 and →r2, respectively. Which of the following should be satisfied for the collision of the point masses?
→r1−→r2|→r2−→r1|=→v2−→v1|→v2−→v1|
→r2−→r1|→r2−→r1|=→v2−→v1|→v2−→v1|
→r2−→r1|→r2+→r1|=→v2−→v1|→v2+→v1|
→r2−→r1|→r2+→r1|=→v2−→v1|→v2+→v1|
The correct Answer is:B
To determine the condition for the collision of two point masses moving with uniform velocities, we can follow these steps:
1. Define the Initial Conditions:
Let the initial position vectors of the two point masses be represented as:
- →r1 for mass 1
- →r2 for mass 2
Their velocities are given as:
- →v1 for mass 1
- →v2 for mass 2
2. Write the Position Vector Equations:
The position of each mass at time t can be expressed as:
- For mass 1: →r1(t)=→r1+→v1t
- For mass 2: →r2(t)=→r2+→v2t
3. Set the Condition for Collision:
For the two masses to collide, their position vectors must be equal at some time t:
→r1+→v1t=→r2+→v2t
4. Rearranging the Equation:
Rearranging the above equation gives:
→r1−→r2=(→v2−→v1)t
5. Expressing in Terms of Vectors:
We can express the left-hand side as:
→r1−→r2=→d(where →d is the vector from mass 2 to mass 1)
And the right-hand side as:
(→v2−→v1)t
6. Finding the Relationship:
To find a relationship between the vectors, we can equate the directions:
→d|→d|=→v2−→v1|→v2−→v1|
7. Final Condition:
Thus, the condition for collision can be summarized as:
→r1−→r2|→r1−→r2|=→v2−→v1|→v2−→v1|
Let the initial position vectors of the two point masses be represented as:
- →r1 for mass 1
- →r2 for mass 2
- →v1 for mass 1
- →v2 for mass 2
The position of each mass at time t can be expressed as:
- For mass 1: →r1(t)=→r1+→v1t
- For mass 2: →r2(t)=→r2+→v2t
For the two masses to collide, their position vectors must be equal at some time t:
→r1+→v1t=→r2+→v2t
Rearranging the above equation gives:
→r1−→r2=(→v2−→v1)t
We can express the left-hand side as:
→r1−→r2=→d(where →d is the vector from mass 2 to mass 1)
And the right-hand side as:
(→v2−→v1)t
To find a relationship between the vectors, we can equate the directions:
→d|→d|=→v2−→v1|→v2−→v1|
Thus, the condition for collision can be summarized as:
→r1−→r2|→r1−→r2|=→v2−→v1|→v2−→v1|
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Subjective28videos
VECTORS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)4videos
WORK, POWER & ENERGY
Similar Questions
Two particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionTwo forces →F1=500N due east and →F2=250N due north have their common initial point. →F2−→F1 is
View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
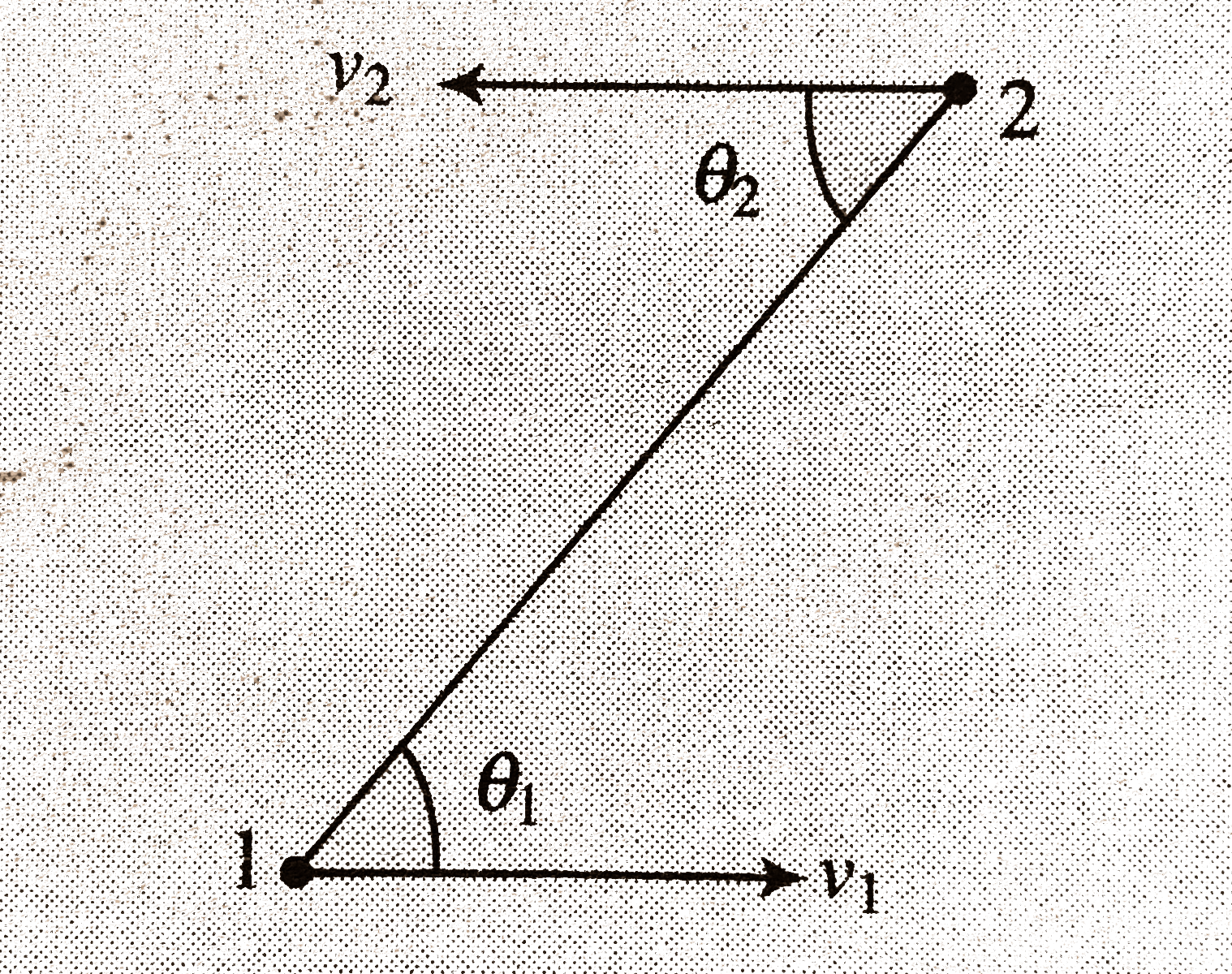 .View Solution
.View SolutionIf a and b are position vectors of A and B respectively the position vector of a point C on AB produced such that −−→AC=3−−→AB is
View SolutionIf →a and →b are position vectors of A and B respectively, then the position vector of a point C in −−→AB produced such that −−→AC =2015 −−→AB is
View SolutionP and Q are two points with position vectors 3→a−2→b and →a+→b respectively. Write the position vector of a point R which divides the line segment PQ in the ratio 2:1 externally.
View SolutionIf →aand→b are position vectors of points AandB respectively, then find the position vector of points of trisection of AB .
View SolutionFind the position vector of a point R which divides the line joining two points P and Q whose position vectors are (2 →a+→b) and (→a− 3→b) respectively, externally in the ratio 1:2.Also, show that P is the mid-point of the line segment RQ.
View SolutionAn impulse →I changes the velocity of a particle from →v1 to →v2. Kinetic energy gained by the particle is :-
View SolutionThe position vectors of P and Q are respectively →aand→b. If R is a point on −−→PQ such that −−→PR=5−−→PQ, then the position vector of R, is
View Solution

