An open vessel containing the liquid upto a height of 15 m. A small hole is made at height of 10 m from the base of the vessel then the initial velocity of efflux is (g = 10 m/s2)
1 m/s
10√2ms
5 m/s
10 m/s
The correct Answer is:D
To find the initial velocity of efflux of the liquid from the hole in the vessel, we can use Bernoulli's equation. Here’s a step-by-step solution:
Step 1: Identify the heights
The total height of the liquid in the vessel is given as 15 m. The hole is made at a height of 10 m from the base. Therefore, the height of the liquid column above the hole is:
h=15m−10m=5m
Step 2: Apply Bernoulli's equation
According to Bernoulli's principle, the sum of pressure energy, potential energy, and kinetic energy per unit volume is constant. We can apply Bernoulli's equation between two points:
- Point 1: At the surface of the liquid (where the velocity is negligible)
- Point 2: At the hole (where the liquid is exiting)
The equation can be written as:
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
Step 3: Assign values to the equation
At point 1 (surface of the liquid):
- Pressure P1=P0 (atmospheric pressure)
- Height h1=5m (height of liquid above the hole)
- Velocity v1=0 (negligible)
At point 2 (the hole):
- Pressure P2=P0 (atmospheric pressure)
- Height h2=0 (reference level at the hole)
- Velocity v2=ve (efflux velocity)
Substituting these values into Bernoulli's equation gives:
P0+ρg(5)+0=P0+0+12ρv2e
Step 4: Simplify the equation
Canceling P0 from both sides:
ρg(5)=12ρv2e
Dividing both sides by ρ:
g(5)=12v2e
Step 5: Solve for ve
Rearranging the equation gives:
v2e=2g(5)
ve=√2g(5)
Step 6: Substitute the value of g
Given g=10m/s2:
ve=√2×10×5
ve=√100
ve=10m/s
Final Answer
The initial velocity of efflux is:
10m/s
---
The total height of the liquid in the vessel is given as 15 m. The hole is made at a height of 10 m from the base. Therefore, the height of the liquid column above the hole is:
h=15m−10m=5m
According to Bernoulli's principle, the sum of pressure energy, potential energy, and kinetic energy per unit volume is constant. We can apply Bernoulli's equation between two points:
- Point 1: At the surface of the liquid (where the velocity is negligible)
- Point 2: At the hole (where the liquid is exiting)
P1+ρgh1+12ρv21=P2+ρgh2+12ρv22
At point 1 (surface of the liquid):
- Pressure P1=P0 (atmospheric pressure)
- Height h1=5m (height of liquid above the hole)
- Velocity v1=0 (negligible)
- Pressure P2=P0 (atmospheric pressure)
- Height h2=0 (reference level at the hole)
- Velocity v2=ve (efflux velocity)
P0+ρg(5)+0=P0+0+12ρv2e
Canceling P0 from both sides:
ρg(5)=12ρv2e
g(5)=12v2e
Rearranging the equation gives:
v2e=2g(5)
ve=√2g(5)
Given g=10m/s2:
ve=√2×10×5
ve=√100
ve=10m/s
The initial velocity of efflux is:
10m/s
Topper's Solved these Questions
Similar Questions
A body is projected with an initial Velocity 20 m/s at 60° to the horizontal. Its initial velocity vector is- (g=10 m/s2)
View SolutionA body of mass 2 kg is dropped from rest from a height 20 m from the surface of Earth. The body hits the ground with velocity 10 m/s, then work done: (g=10m/s2)
View Solution
Knowledge Check
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
An open vessel contains water upto height 50 cm in it. What is the velocity of efflux through an orifice at height 30 cm above the bottom level ? [Take g = 10 m/s2]
View SolutionIn a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x

View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
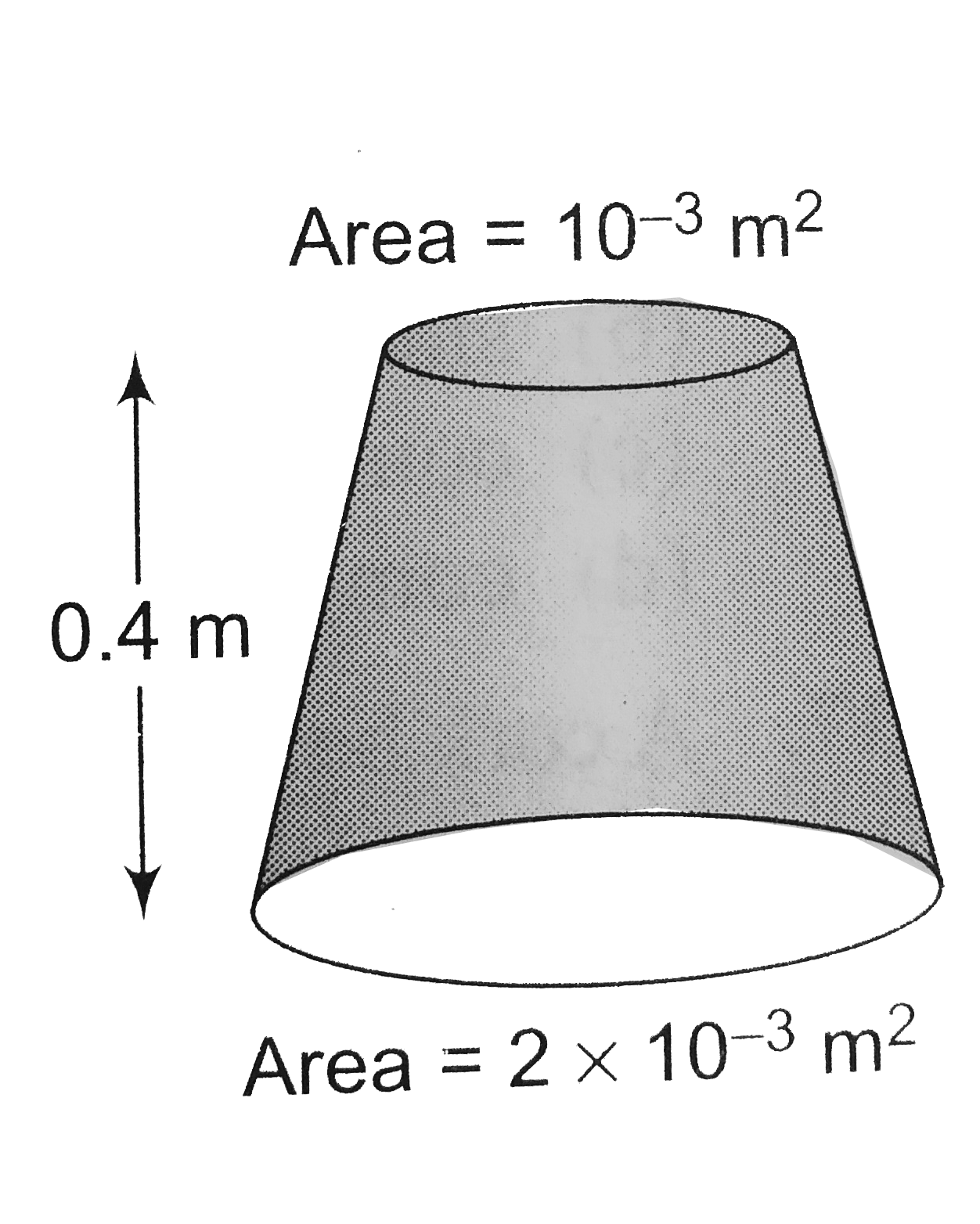
View SolutionA small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration a0=g2. Time taken by the block to reach the surface, if it is released with zero initial velocity is (g=10m/s2)
View SolutionLiquid is filled in a vessel of square base (2m×2m) upto a height of 2m as shown in figure (i). In figure (ii) the vessel is tilted from horizontal at 30∘.

What is the velocity of efflux in this case. Liquid does not spills out?
View Solution
