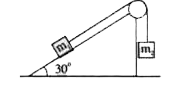
In fig.block A and B are connected together by a string and placed on a smooth inclined plane. B is connected to C(which is suspended vertically) by another string which passes over a smooth pulley fixed to th plane. The mass A is mA=1 kg and mass of B is mB=2kg.

(a) If the system is at rest, find the mass of C.
(b) If the mass of C is twice the mass calculate in (a) then find the acceleration of the system.
(a) From the free-body diagram of A :
T1: Tension in string betwwne A and B
NA: Normal reaction between A and incline
As A is at rest, net force parallel and perpendivular to inclined should be balanced.
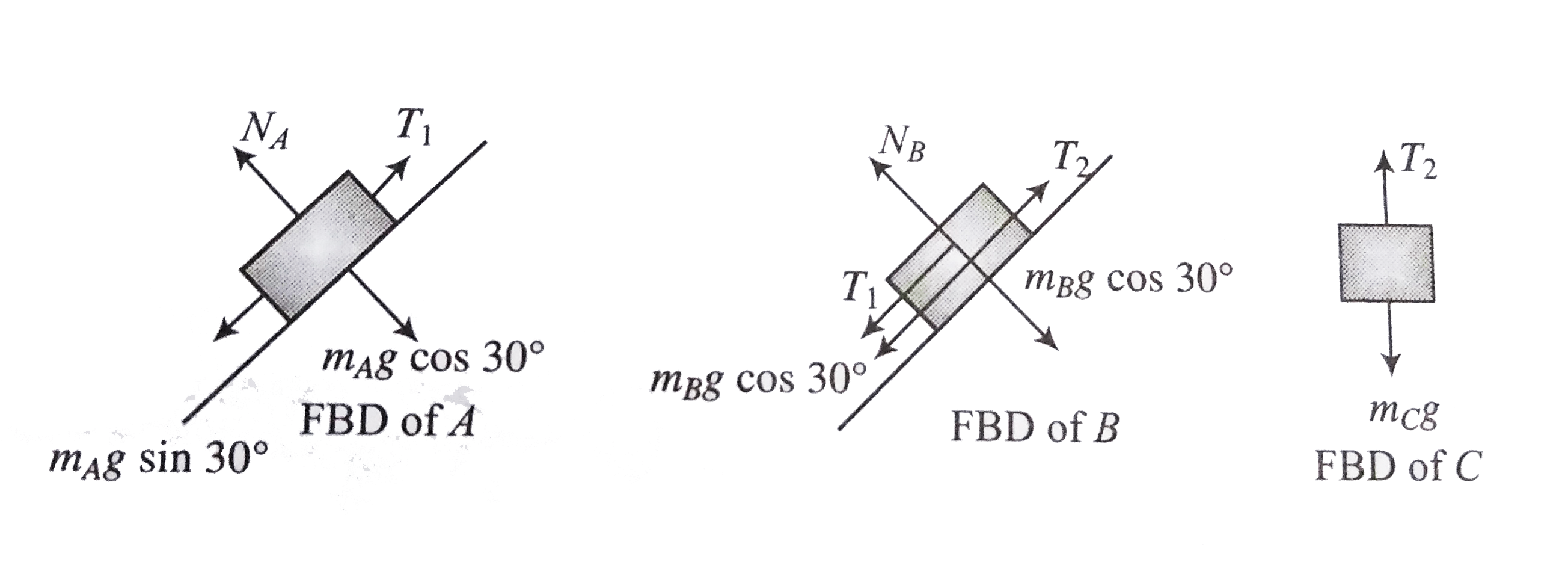
NA=mAgcosθ=10cos30∘=5√3N
T1=mAgsinθ=10sin30∘=5N
From the free-body diagram of B:
As B is connected to both strings, two tensions T1 and T2 will act on it.
T2 is the tension (force) of string between B and C acting upwards.
T1 is the tension of string between A and B acting downwards
Balancing forces:
NB=mBgcos30∘=20cos30∘=10√3N
T2=T1+mBgsin30∘=5+20sin30∘
=5+20×12=15N
Force diagram of C:
T2 is the pulling force of string on block C, therefore, mCg=T2, hence MC=1.5kg
(b) In this case, mass of C=3kg
Let the acceleration of the system be a. We can assume arbitrary direction of motion. Let the blocks move up the incline and block C move downward.
From FBD of A: T1−10sin30∘=1a ...(i)
From FBD of : T2−T1−20sin30∘=2a ...(ii)
From FBD of C: 30−T2=3a ...(iii)
Solving (i), (ii) and (iii) , a=2.5ms−2 .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionA light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
View SolutionThe figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.
 View Solution
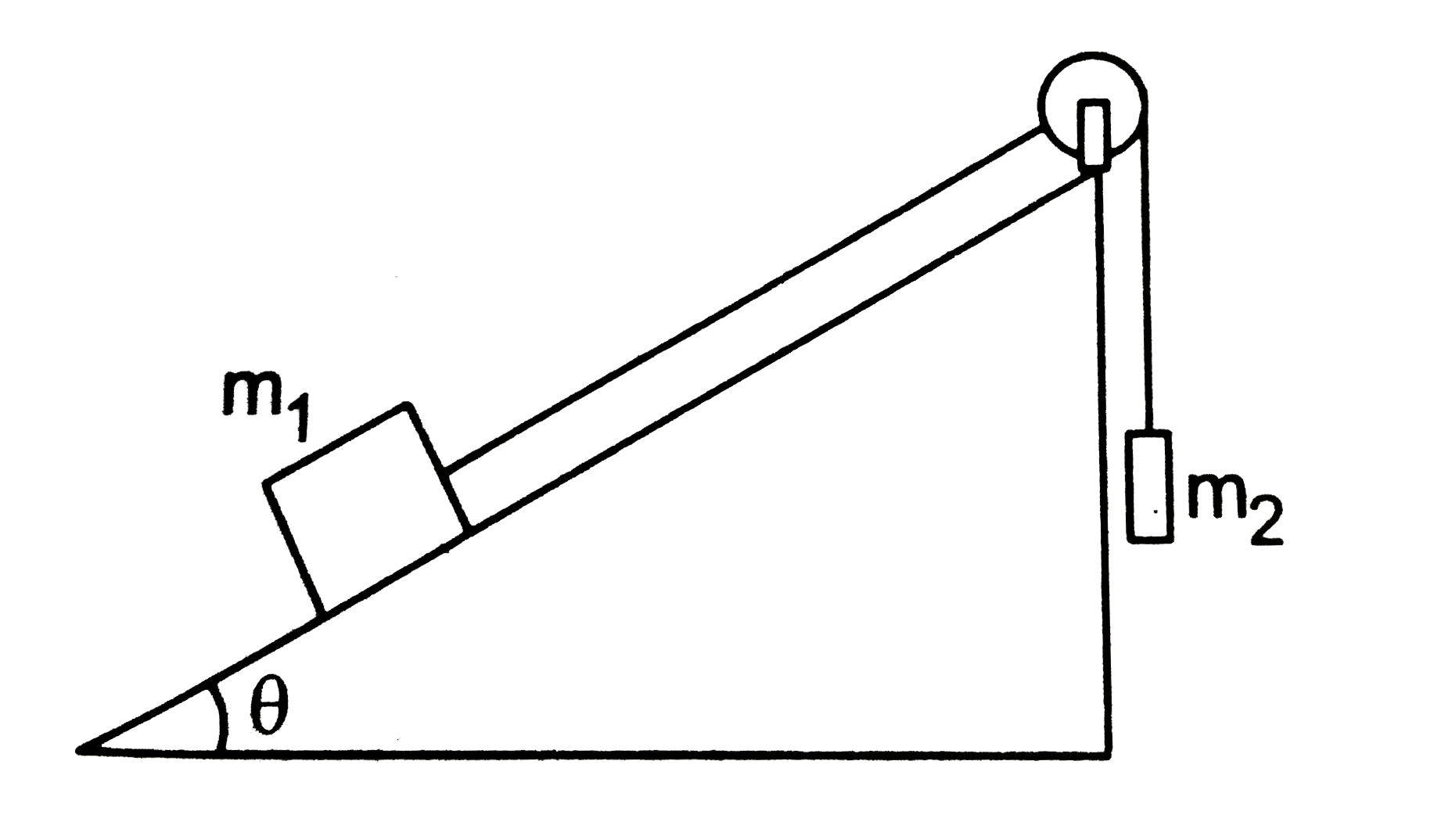
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
 View Solution
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionBlock A has mass 40kg and B has 15kg and F is 500N parallel to smooth inclined plane.The system is moving together
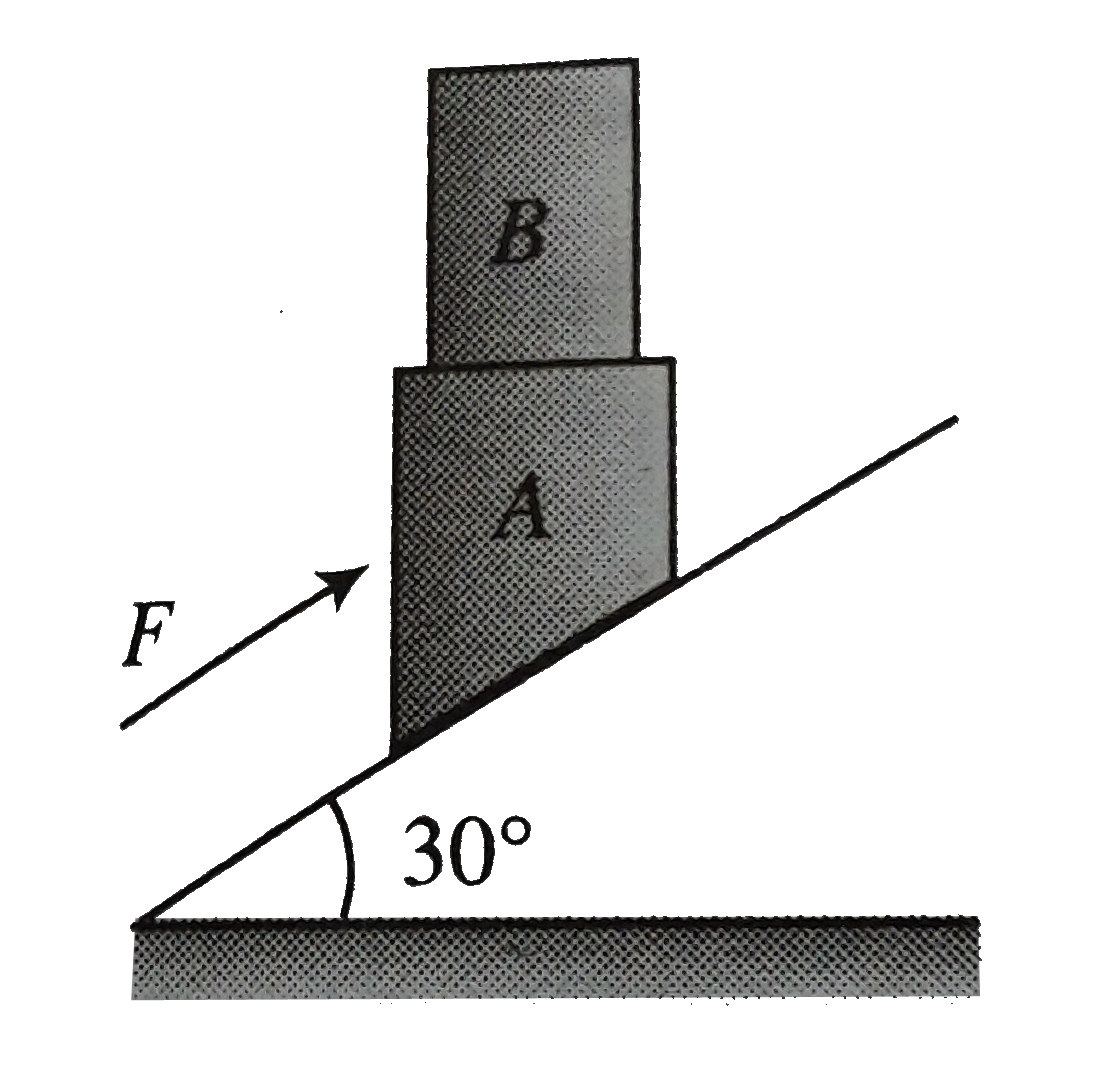
The acceleration of the system isView SolutionA block of mass m1 = 4kg lying on a plane inclined at an angle of 30∘, is connected to another freely suspended block of mass m2 = 6kg with the help of a string passing over a smooth pulley as shown in the figure. The acceleration of each block is (g = 10 m/s2)
 View Solution
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
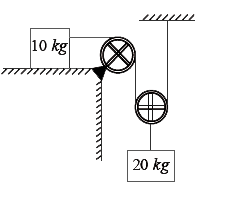 View Solution
View SolutionA bead B of mass 'm' can travel without frictionn on a smooth horizontalwire xx′. The bead is connected to a block of identical mass by an ideal string passing over an ideal pulley. The system, as shown, is in vertical plane.

The system is allowed to fall. Find the speed of block A at the instant when string connected to the bead B makes an angle 37∘ with vertical.View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View Solution

