Two particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
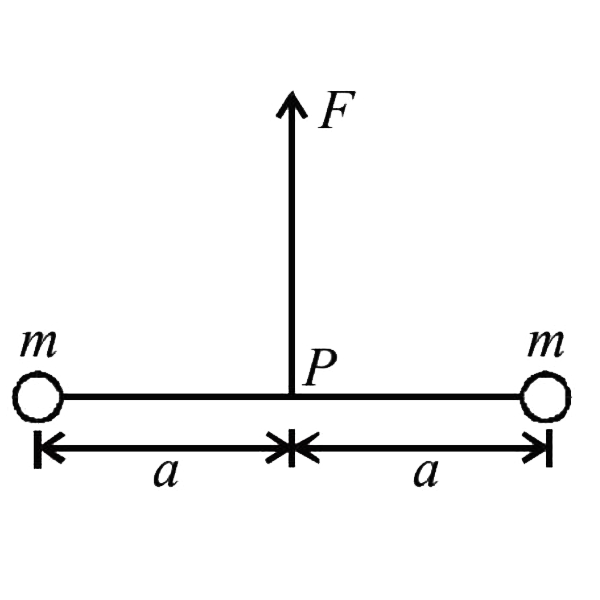
Let the tension in the string be T at any angular position θ. The acceleration of each ball along x and y axes be a and a1, respectively. Writing the equation of motion of m, we obtain
ΣFx=ma⇒Tcosθ=ma ..(i)
ΣFy=ma1⇒Tsinθ=ma1 ...(ii)
At point P, as it is accelerating with an acceleration a, therefore F−2tcosθ=mPa
Where mp=mass of the string at the point P≅0
⇒F=2Tcosθ ..(iii)
(ii)÷(iii)⇒tanθ=a1a
⇒a1=atanθ, where a=Tcosθm from (i).
Putting T=F2cosθ from (3), we obtain
a1=F2mtanθ.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.413videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Two bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
 View Solution
View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is
 View Solution
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then
 View Solution
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then
 View Solution
View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is
 View Solution
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then
 View Solution
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution

