A particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then
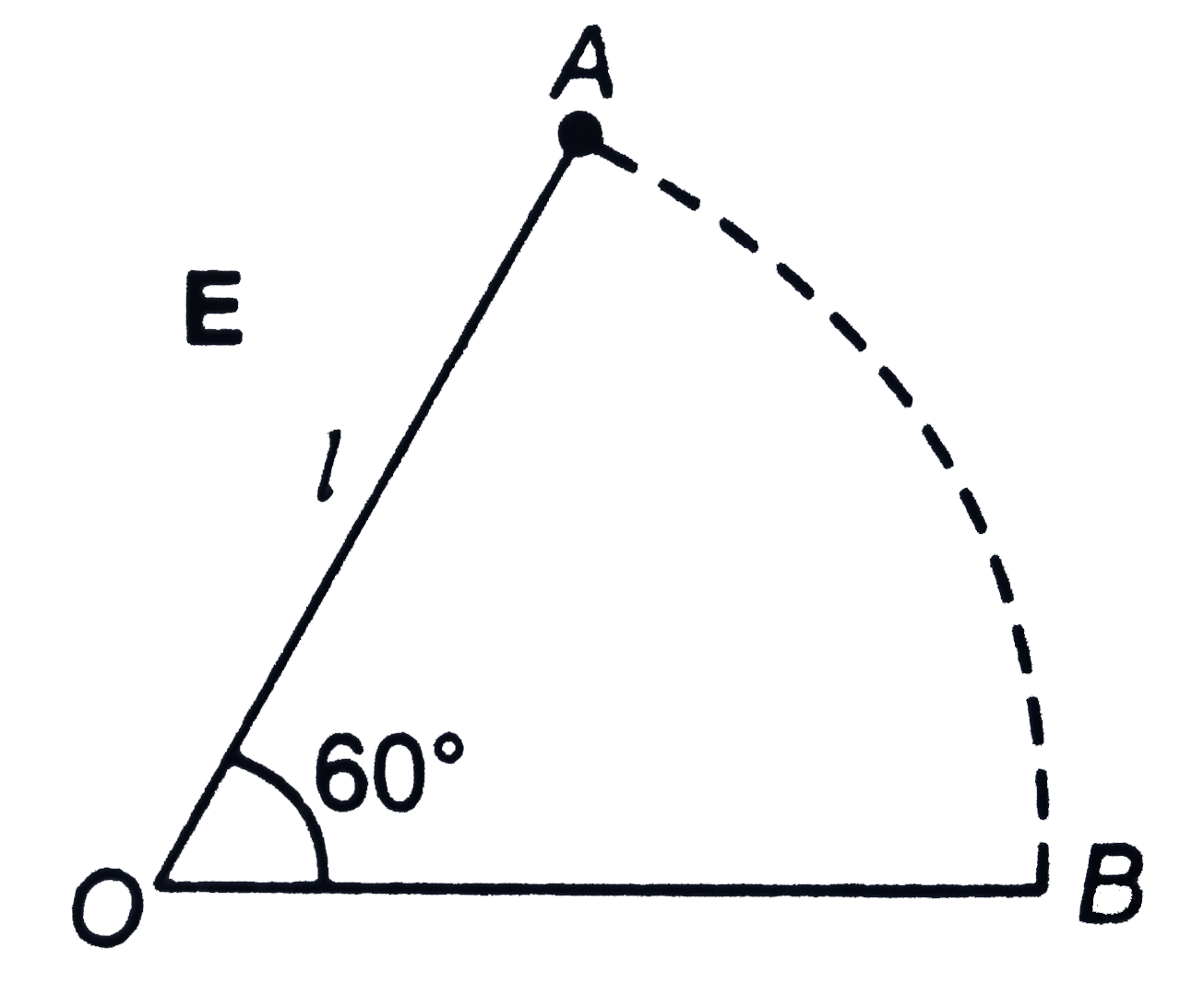
the speed of the particle when it reaches B is √2qElm
the speed of the particle when t reaches B is √qElm
the tension in the string when particles reaches at B is 2qE
the tension in the string when the particle reaches at B is zero
The correct Answer is:B, C
Work done by tension = 0
Work done by Electric field
=−qE×/(1−cos60∘)
(B)qEl2=12mV2⇒V=√qElm
(C)T−qE=mV2l⇒T=2qE
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.40
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.41
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.38
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A particle of mass m1 is fastened to one end of a string and one of m2 to the middle point, the other end of the string being fastened to a fixed point on a smooth horizontal table The particles are then projected, so that the two portions of the string are always in the same straight line and describes horizontal circles find the ratio of tensions in the two parts of the string

View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View Solution
Knowledge Check
Two identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.
 AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
The maximum angle made by the string with downward vertical is
View SolutionA particle of mass 'm' is attached to one end of a string of length 'l' while the other end is fixed to a point 'h' above the horizontal table, the particle is made to revolve in a circle on the table, so as to make P revolution per sec. The maximum value of P if the particle is to be contact with the table is
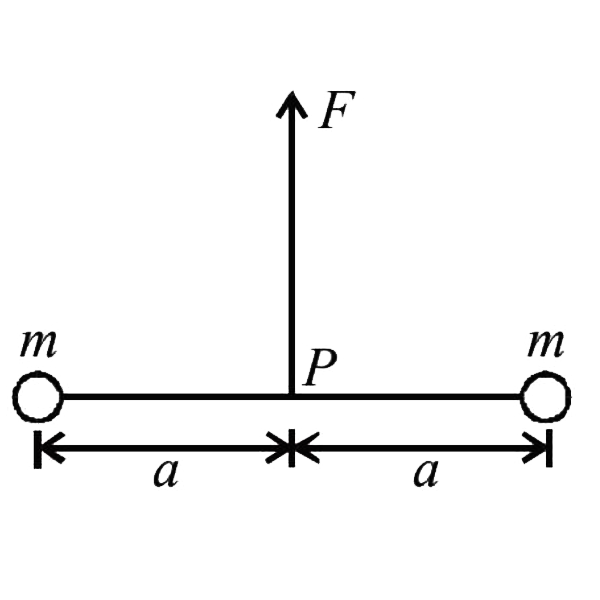
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
View SolutionTwo balls having masses m and 2m are fastened to two light strings of same length shown in the figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. (a). Find velocities of the balls just after their collision. (b). How high will the balls rise after the collision.

View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA heavy particle is tied to the end A of a string of the length1.6 m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60∘ with the horizontal. Then,
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View Solution