Two beads of equal masses m are attached by a string of length √2a and are free to move in a smooth circular ring lying in a vertical plane as shown in figure. Here a is the radius of the ring. Find the tension and acceleration of B just offer the heads are released to move.

Zero
mg
√2mg
mg/√2
The correct Answer is:D
As shown in fig. from FBD of A,
Tcos45∘=ma …(i)
From FBD of B:
Mg−Tcos45∘=ma..(ii)
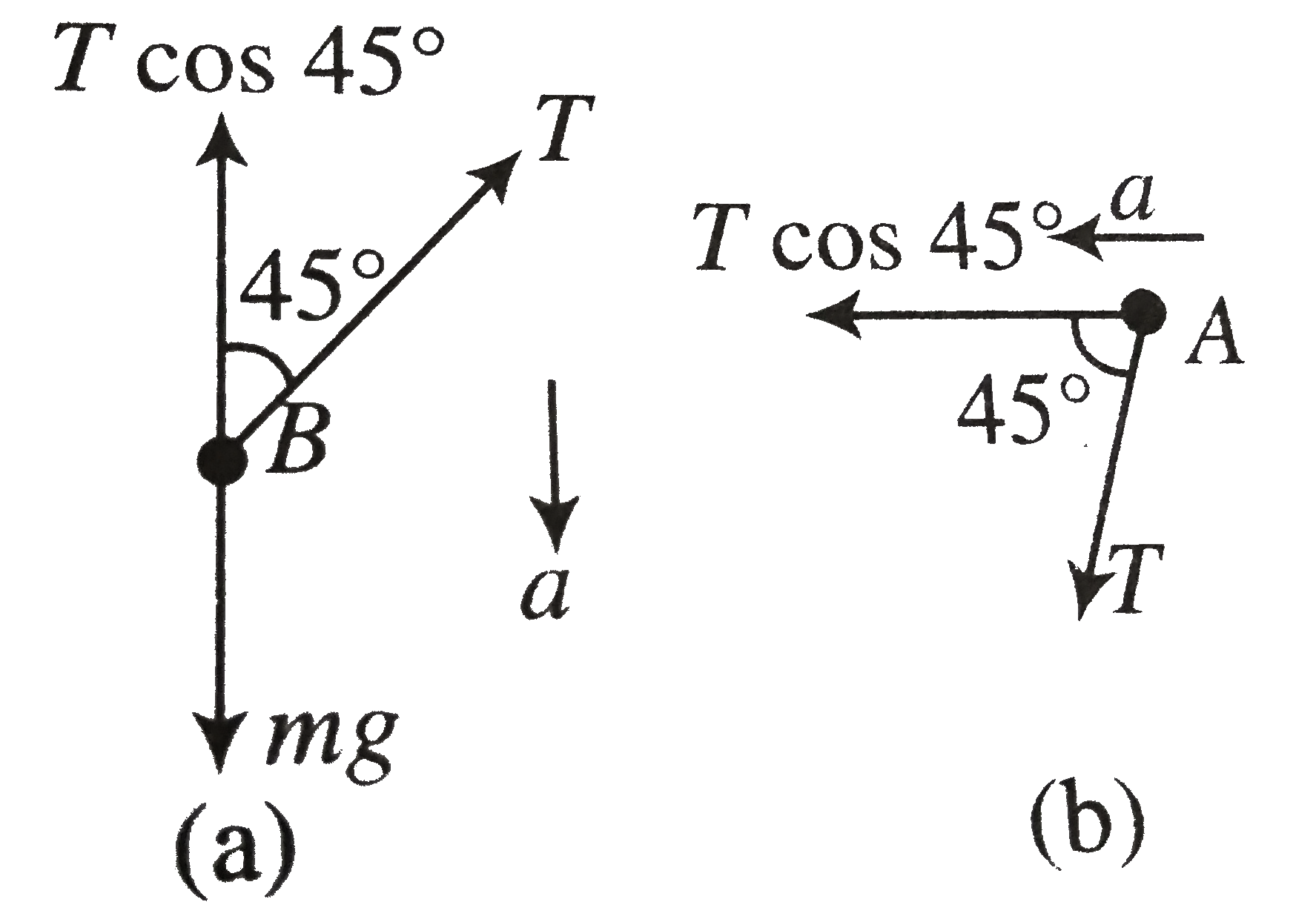
From (i) and (ii) we get T=mg/√2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
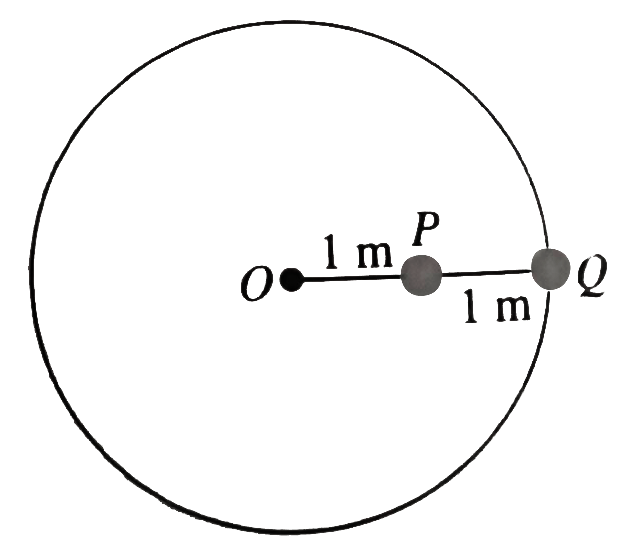
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio of their tension:
View SolutionA uniform string of length 10m and mass 20 kg lies on a smooth frictionless inclined plane. A force of 200N is applied as shown in the figure.

(a) Find the acceleration of the string.
(b) Find the tension in the string at 2m from end A.
View SolutionTwo beads of masses m1 and m2 are connected to each other by massless string. Both beads are free to mover over fixed smooth circular loop in vertical plane. At any instant they are in the position shown and subtends angle 90∘ at centre. Find tangential accelerations of both beads and tension in the string if string remains taut.

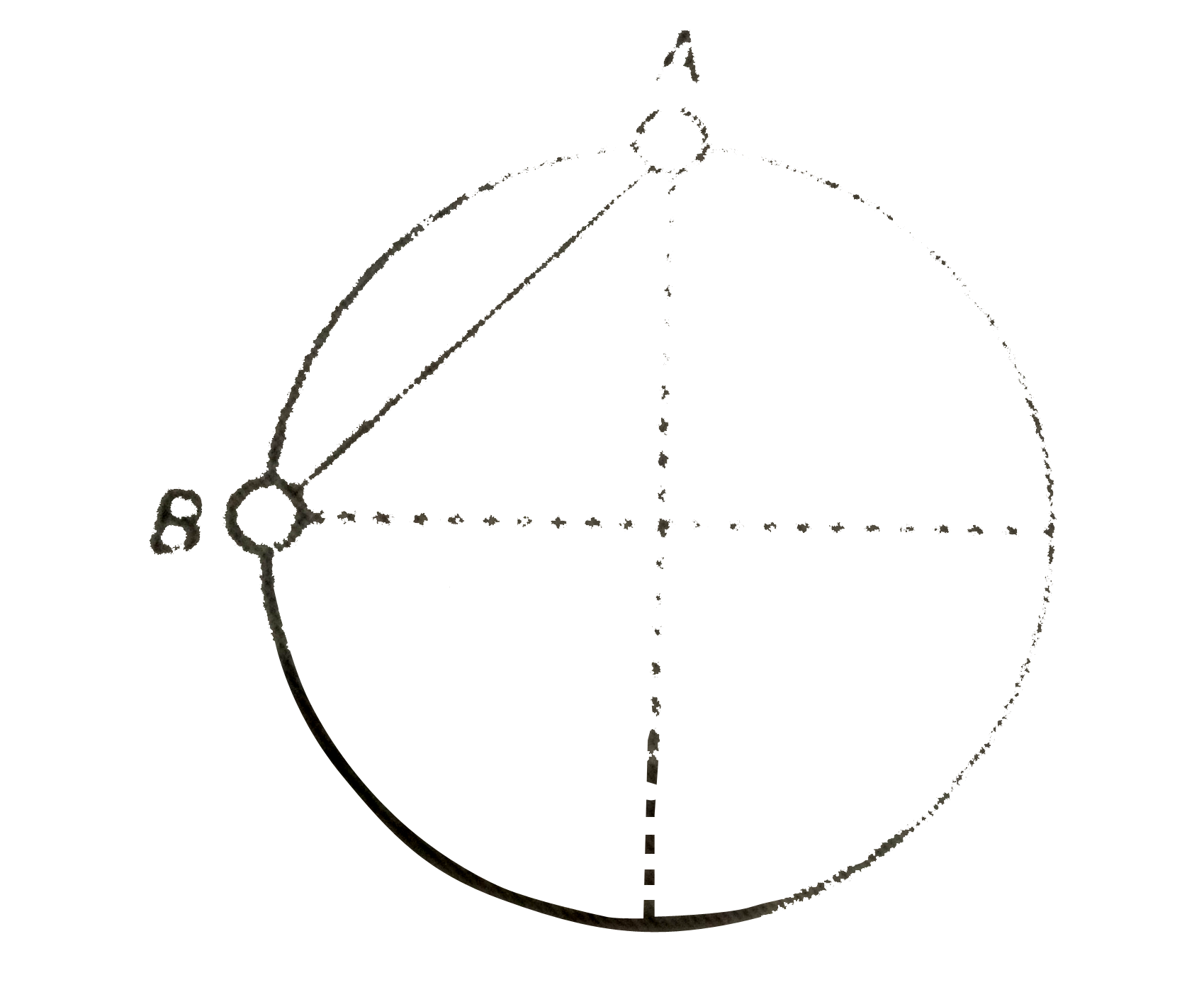
View SolutionTwo beads A and B of equal mass m are connected by a light inextensibe chord. They are constrined to move on a frictionless ring in vertical plane. The blocks are released from rest as shown in figure. The tension in the chord just after the release is
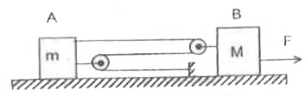
View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.
View SolutionTwo beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )
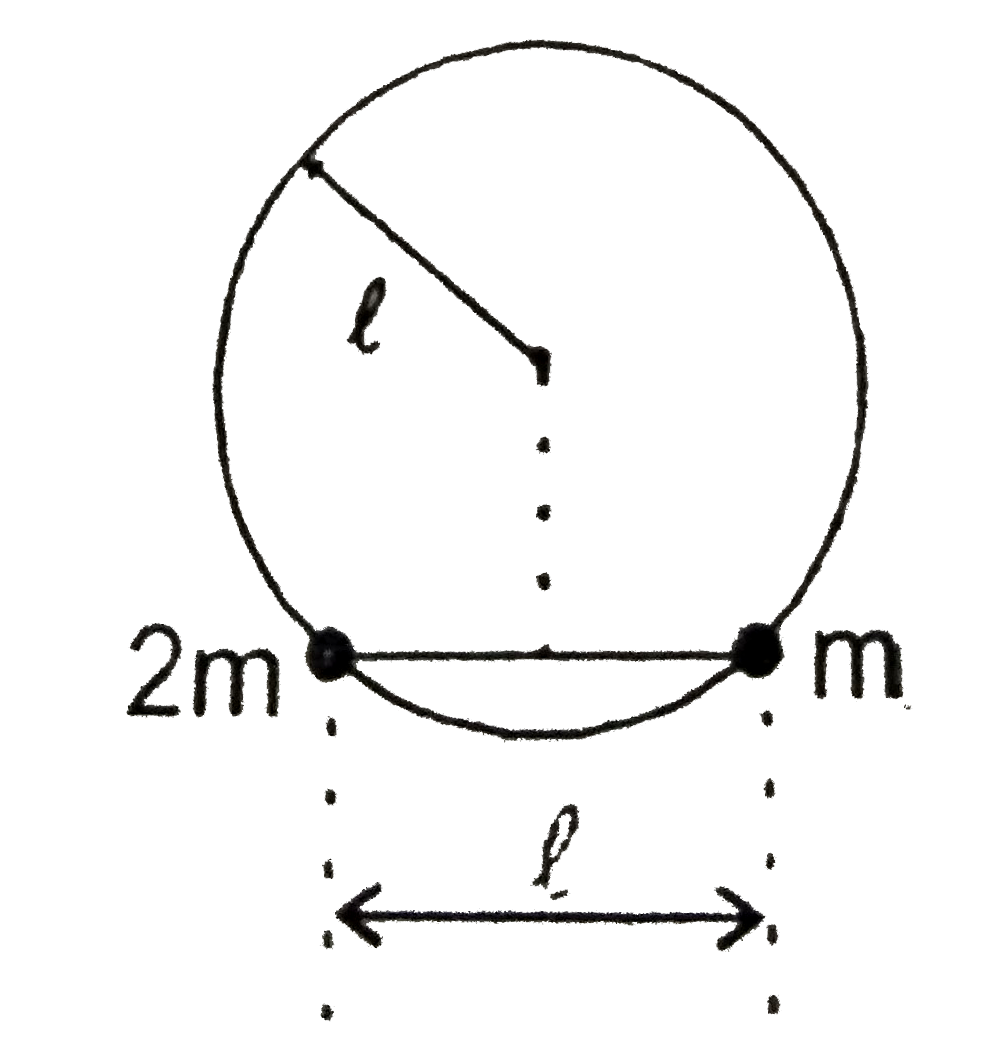
If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :
View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
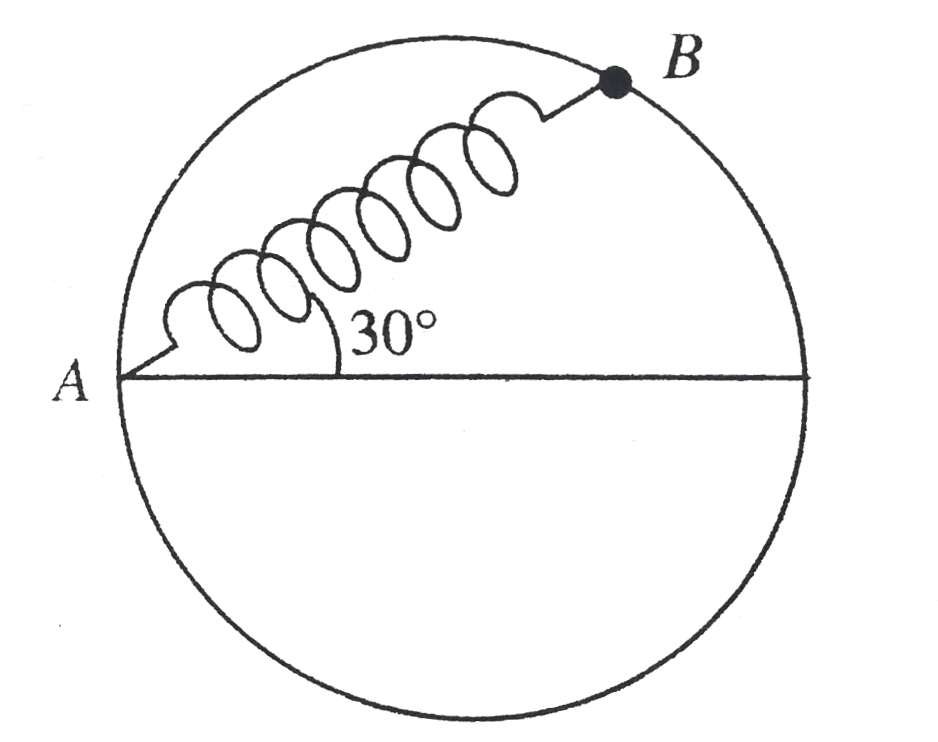
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View Solution
