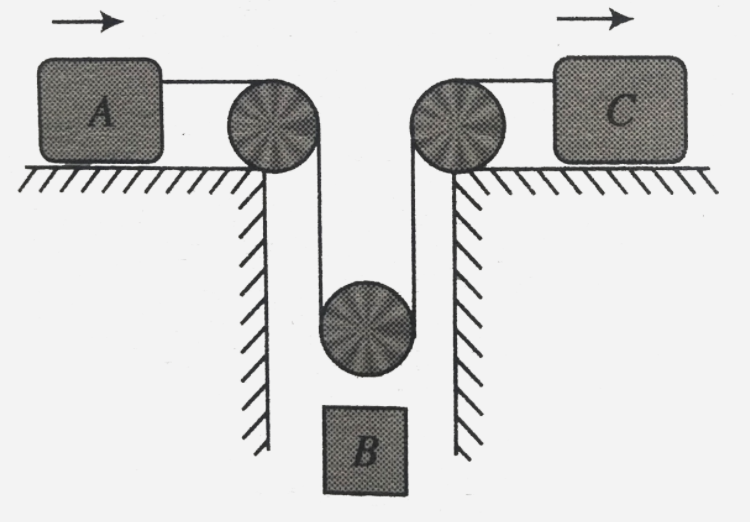
Block A and C starts from rest and move to the right with acceleration $a_{A} = 12 t m s^{- 2}$ and $a_{C} = 3 m s^{- 2}$ . Here t is in second. The time when block B again comes to rest is

A

2s

B

1s

C

$3 / 2 s$

D

$1 / 2 s$

Text Solution

Verified by Experts

The correct Answer is:D

From constraint relation we can see that the acceleration of block B in upward direction is
$a_{B} = (\frac{a_{C} + a_{A}}{2})$ with proper signs
So, $a_{B} = (\frac{3 - 12 t}{2}) = 1.5 - 6 t$
or $\frac{d v_{B}}{d t} = 1.5 - 6 t$ or $v_{B} \int 0 d v_{B} = 1 \int 0 (1.5 - 6 t) d t$
or $v_{B} = 1.5 t - 3 t^{2}$ or $v_{B} = 0$ at $t = 1 / 2 s$ .

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Block A and C start from rest and move to the right with acceleration $a_{A} = 12 t m / s^{2}$ and $a_{C} = 3 m / s^{2}$ Here t is in seconds. The time when block B attain comes to rest is:

A2s
B1s
C $3 / 2 s$
D $1 / 2 s$
Question 2 - Select One
Blocks $m_{1}$ and $m_{2}$ starts from rest and move to right with accelerations as shown. If $t$ is in second then the time when block $m_{3}$ again come to rest from $t = 0$ is (pulley and strings are ideal) :
.
A $\frac{\sqrt{5}}{2} sec$
B $\frac{1 + \sqrt{5}}{2} sec$
C $\frac{1 + \sqrt{3}}{2} sec$
D $1 sec$
Question 3 - Select One
A particle starts from rest with a time varying acceleration $a = (2 t - 4)$ . Here $t$ is in second and $a$ in $m / s^{2}$
The velocity time graph of the particle is
Aparabola passing through origin
Bstraight line not passing through origin
Cparabola not passing through origin
Dstraight line passing through origin

CENGAGE PHYSICS ENGLISH-NEWTON'S LAWS OF MOTION 1-Single Correct

Home
Ask Doubt
Profile