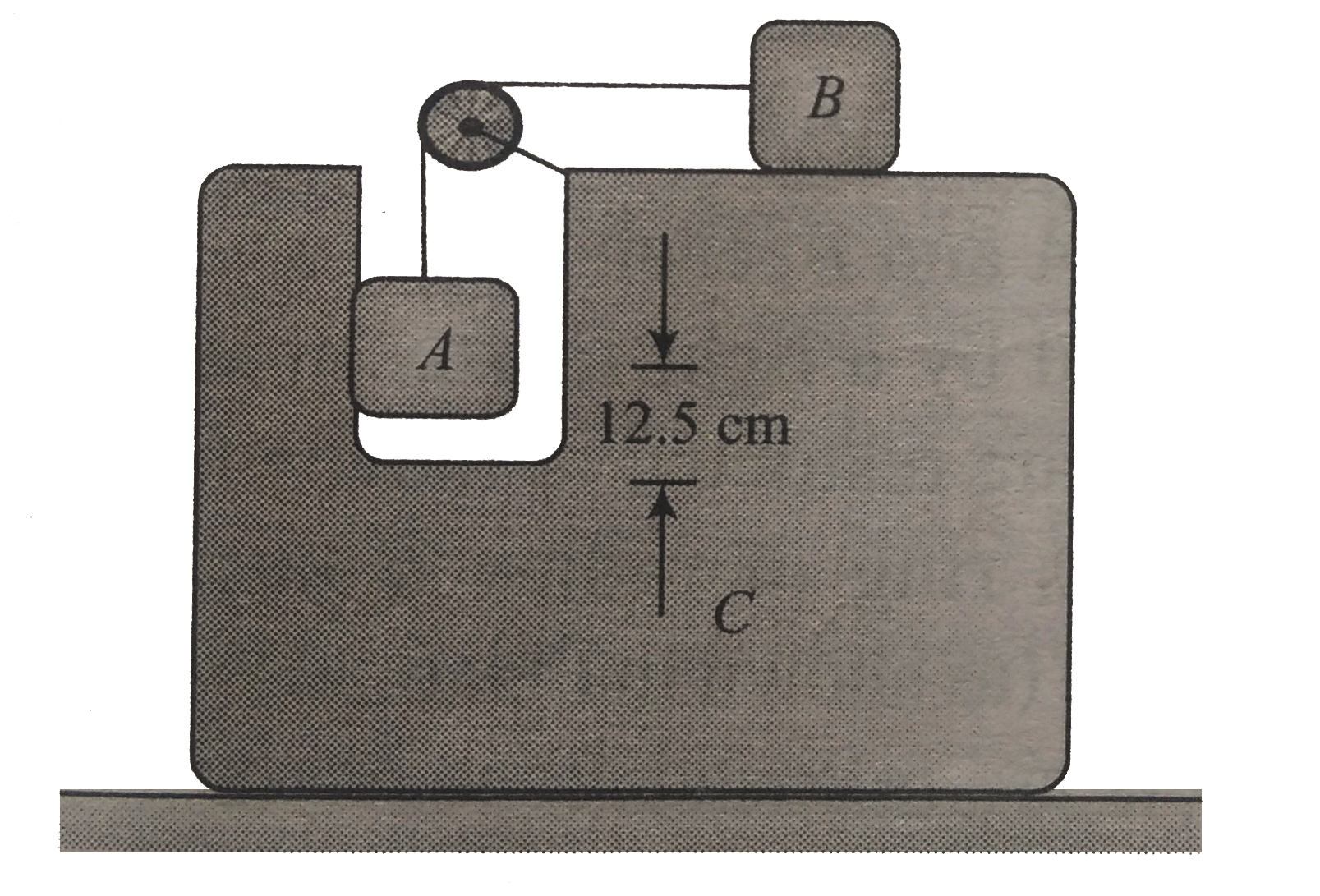
A small, light pulley is attached with a block C of mass 4 kg as shown in fig. Block B of mass 1.5 kg is placed on the top horizontal surface of C. Another block A of mass 2 kg is hanging from a string, attached with B and passing over the pulley. Taking g=10ms−2 and neglecting friction, calculate the acceleration of each block when the system is released from rest.
1/4ms−2
2/7ms−2
5/4ms−2
1/3ms−2
The correct Answer is:C
Let acceleration of block C be a1 (rightwards) and acceleration of block B be a2 (lefwards).
Then acceleration of A will be (a1+a2) downwards and a1 rightwards.
Free body diagram of A is shown in fig.
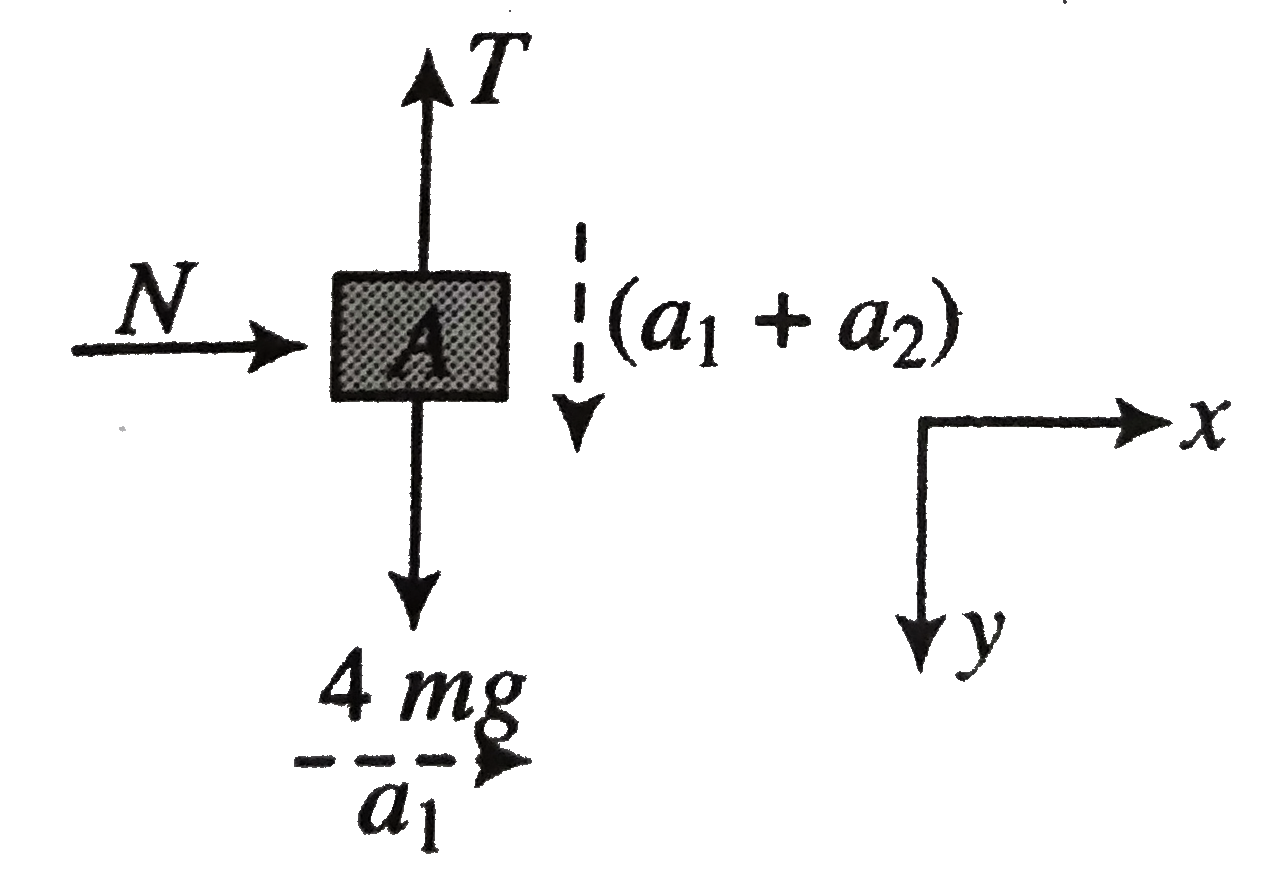
Using ΣFx=max and ΣFy=may, we get
N=4m(a1) ..(i)
and 4mg−T=4m(a1+a2) ..(ii)
Free bocy diagram of B (showing horizontal force only) is shown in the figure.

Using ΣFx=max, we get
T=3ma2 ...(iii)
Free body diagram of C (showing horizontal force only) is shown in fig.
Using ΣFx=max, we get
T−N=8ma1...(iv)
We have four unknowns T,N,a1, and a2. solving these four equations, we get
a1=g8 and a2=g2, a1+a2=58g
Thus, acceleration of A is g/8 in horizontal direction and 5g/8 in vertical direction.
Acceleration of B is g/2 in horizontal direction (leftwards) and acceleration of C is g//8 in horizontal direction (rightwards).
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
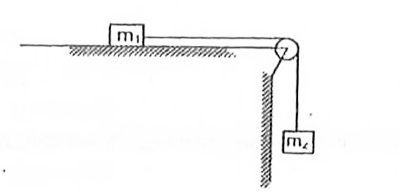
A block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionA block of mass M placed on a frictionless horizontal table is pulled by another block of mass m hanging vertically by a massless string passing over a frictionless pulley. The tension in the string is :
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
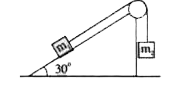
View SolutionA block of mass m1 = 4kg lying on a plane inclined at an angle of 30∘, is connected to another freely suspended block of mass m2 = 6kg with the help of a string passing over a smooth pulley as shown in the figure. The acceleration of each block is (g = 10 m/s2)
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View SolutionA 2kg block lying on smooth table which is connected by a body of mass 1 kg by a string which passes through a pulley. Take 1 kg mass hanging vertically. Find the acceleration of block & tension in string.
View SolutionA wooden block of mass 0.8 kg is dragged along a level frictionless surface by a hanging block of mass 0.2 kg as shown in the figure. Calculate the tension in the string and the acceleration of blocks.
View SolutionFigure shows three blocks of mass m each hanging on a string passing over a pulley. Calculate the tension in the string connecting A to B and B to C?

View Solution
