The ball of mas m moves with speed v againest a smooth , fixed vertical circular groove of radius R kept on smooth horizontal surface find the
a. normal reaction of the floor or the ball.
b. normal reaction of the vertical wall on the ball.
To solve the problem, we will analyze the forces acting on the ball in both the vertical and horizontal directions.
Step 1: Analyze the forces acting on the ball.
- The ball of mass m is moving in a vertical circular groove with a radius R.
- The forces acting on the ball are:
- The gravitational force acting downwards, mg.
- The normal reaction force from the floor, Nfloor, acting upwards.
- The normal reaction force from the wall, Nwall, acting horizontally towards the center of the circular groove.
Step 2: Determine the normal reaction of the floor on the ball.
- Since the ball does not accelerate vertically, we can apply Newton's second law in the vertical direction:
∑Fy=Nfloor−mg=0
- Rearranging gives:
Nfloor=mg
- Thus, the normal reaction of the floor on the ball is Nfloor=mg.
Step 3: Determine the normal reaction of the vertical wall on the ball.
- In the horizontal direction, the ball is undergoing circular motion, which requires a centripetal force.
- The centripetal force is provided by the normal reaction from the wall:
Nwall=mv2R
- Here, v is the speed of the ball and R is the radius of the circular groove.
Final Answers:
a. The normal reaction of the floor on the ball is Nfloor=mg.
b. The normal reaction of the vertical wall on the ball is Nwall=mv2R.
---
- The ball of mass m is moving in a vertical circular groove with a radius R.
- The forces acting on the ball are:
- The gravitational force acting downwards, mg.
- The normal reaction force from the floor, Nfloor, acting upwards.
- The normal reaction force from the wall, Nwall, acting horizontally towards the center of the circular groove.
- Since the ball does not accelerate vertically, we can apply Newton's second law in the vertical direction:
∑Fy=Nfloor−mg=0
- Rearranging gives:
Nfloor=mg
- Thus, the normal reaction of the floor on the ball is Nfloor=mg.
- In the horizontal direction, the ball is undergoing circular motion, which requires a centripetal force.
- The centripetal force is provided by the normal reaction from the wall:
Nwall=mv2R
- Here, v is the speed of the ball and R is the radius of the circular groove.
a. The normal reaction of the floor on the ball is Nfloor=mg.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Figure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
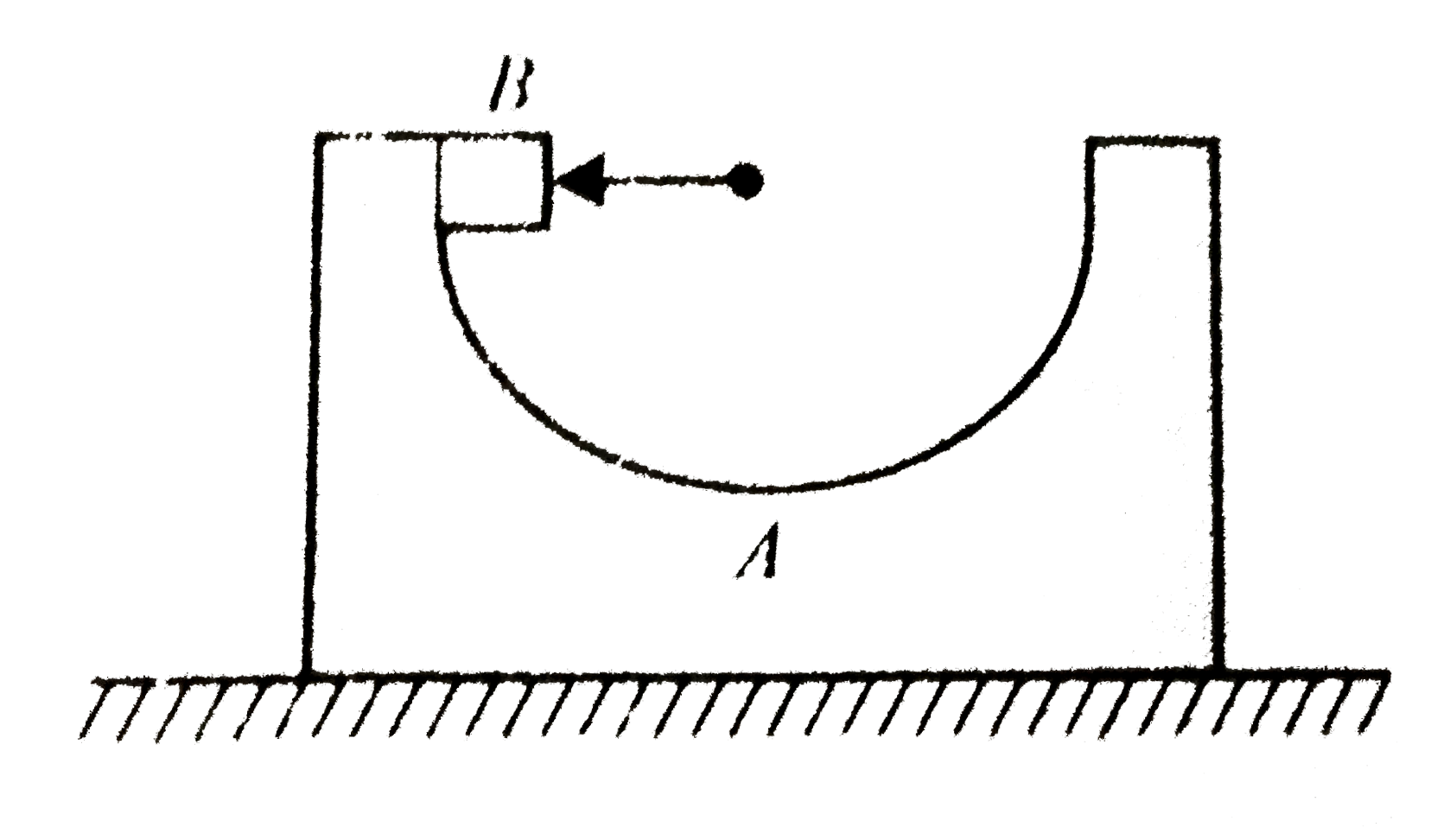 View Solution
View SolutionA ball of mass m when dropped from certain height as shown in diagram, strikes a wedge kept on smooth horizontal surface and move horizontally just after impact. If the ball strikes the ground at a distance d from its initial line of fall, thenthe amplitude of oscillation of wedge after being hit by the ball will be
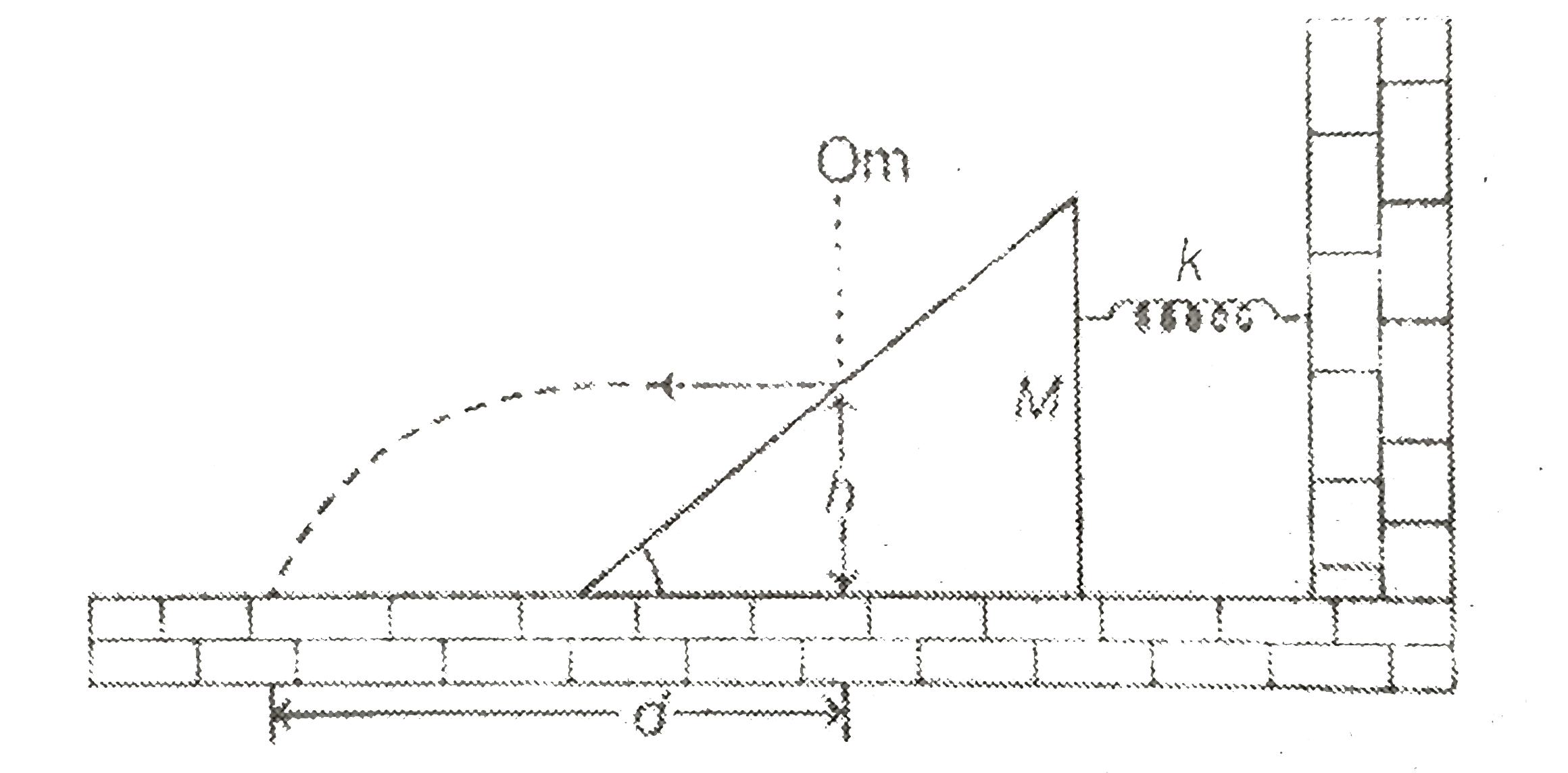 View Solution
View SolutionIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
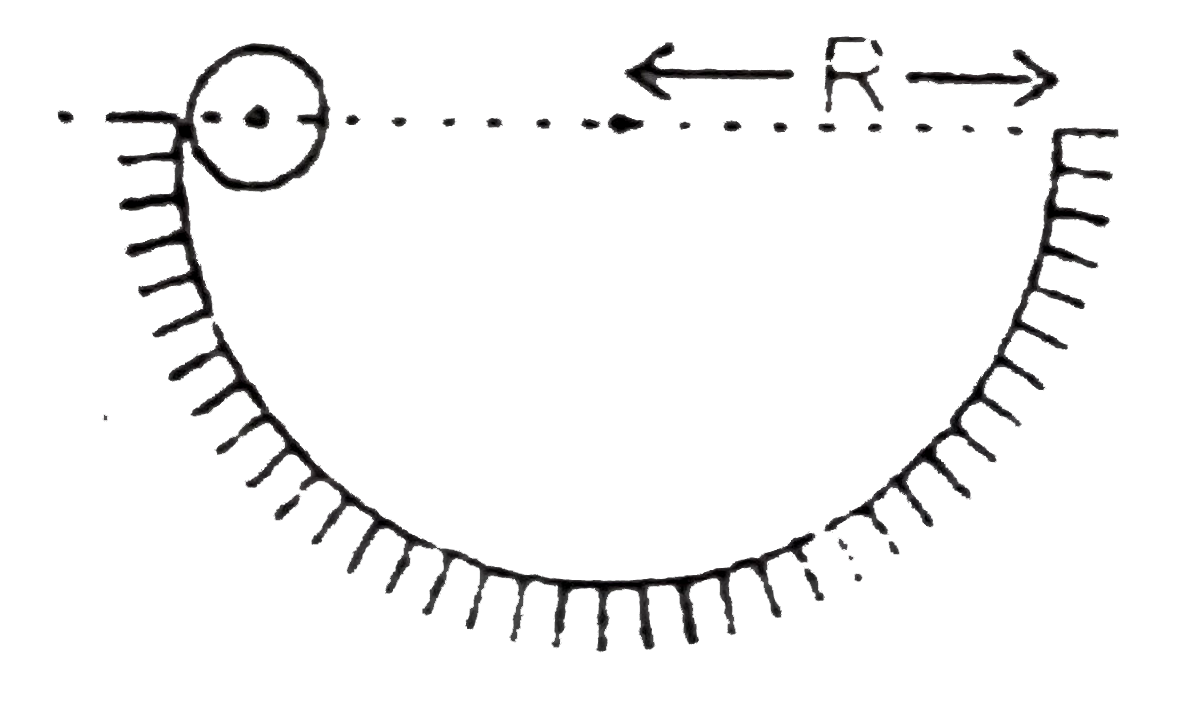 View Solution
View SolutionA ball of mass 'm' is rotating in a circle of radius 'r' with speed v inside a smooth cone as shown in figure. Let N be the normal reaction on the ball by the cone .then choose the wrong option.
 View Solution
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is
 View Solution
View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View SolutionA ball of mass m moves with speed v and stricks a wall having infinite mass and it returns with same speed then the work done by the ball on the wall is
View Solution
A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.View SolutionA small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
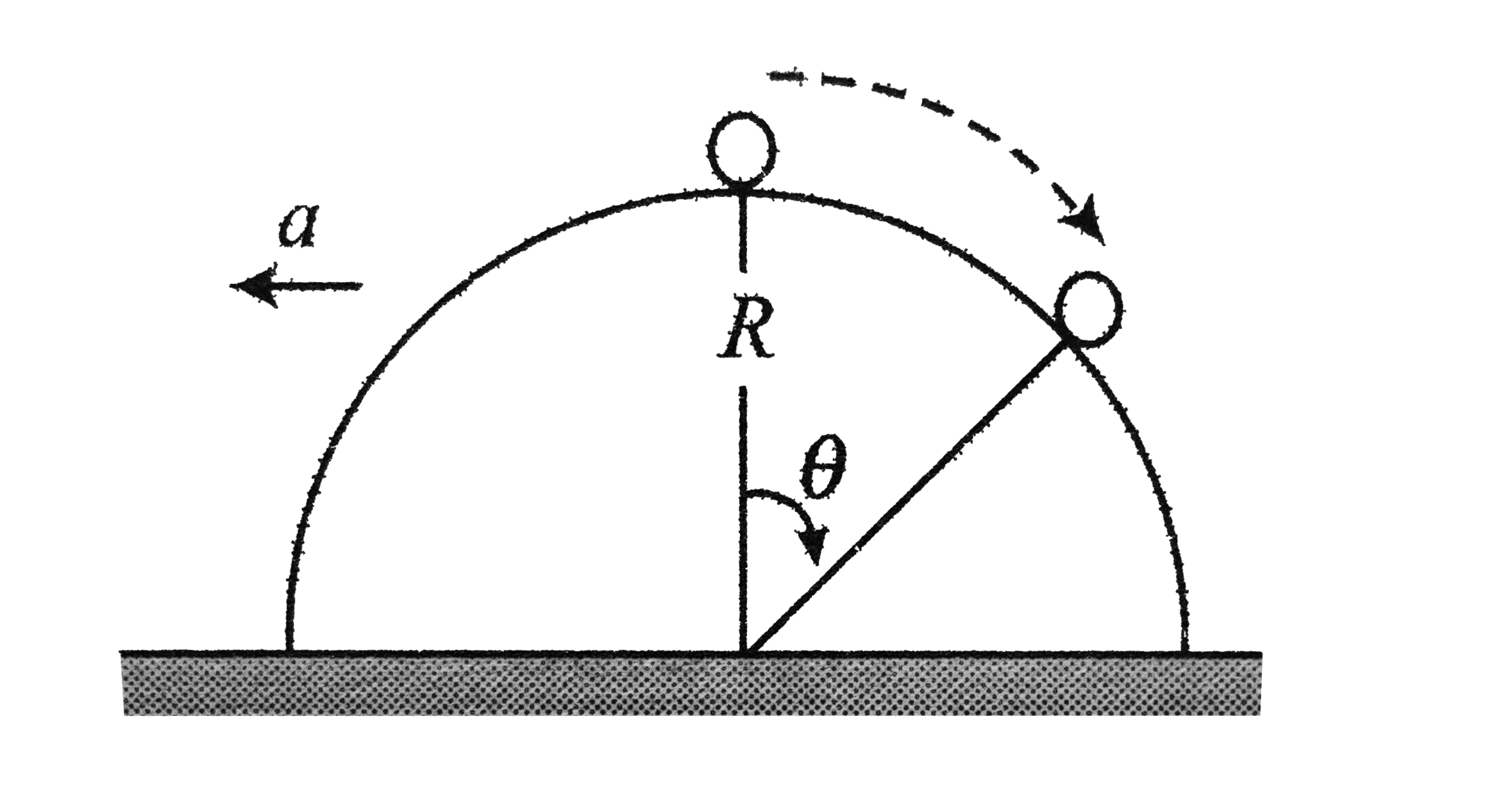 View Solution
View SolutionA ball of mass 'm' is rotating in a circle of radius 'r' with speed v inside a smooth cone as shown in figure. Let N be the normal reaction on the ball by the cone .then choose the wrong option.
 View Solution
View Solution

