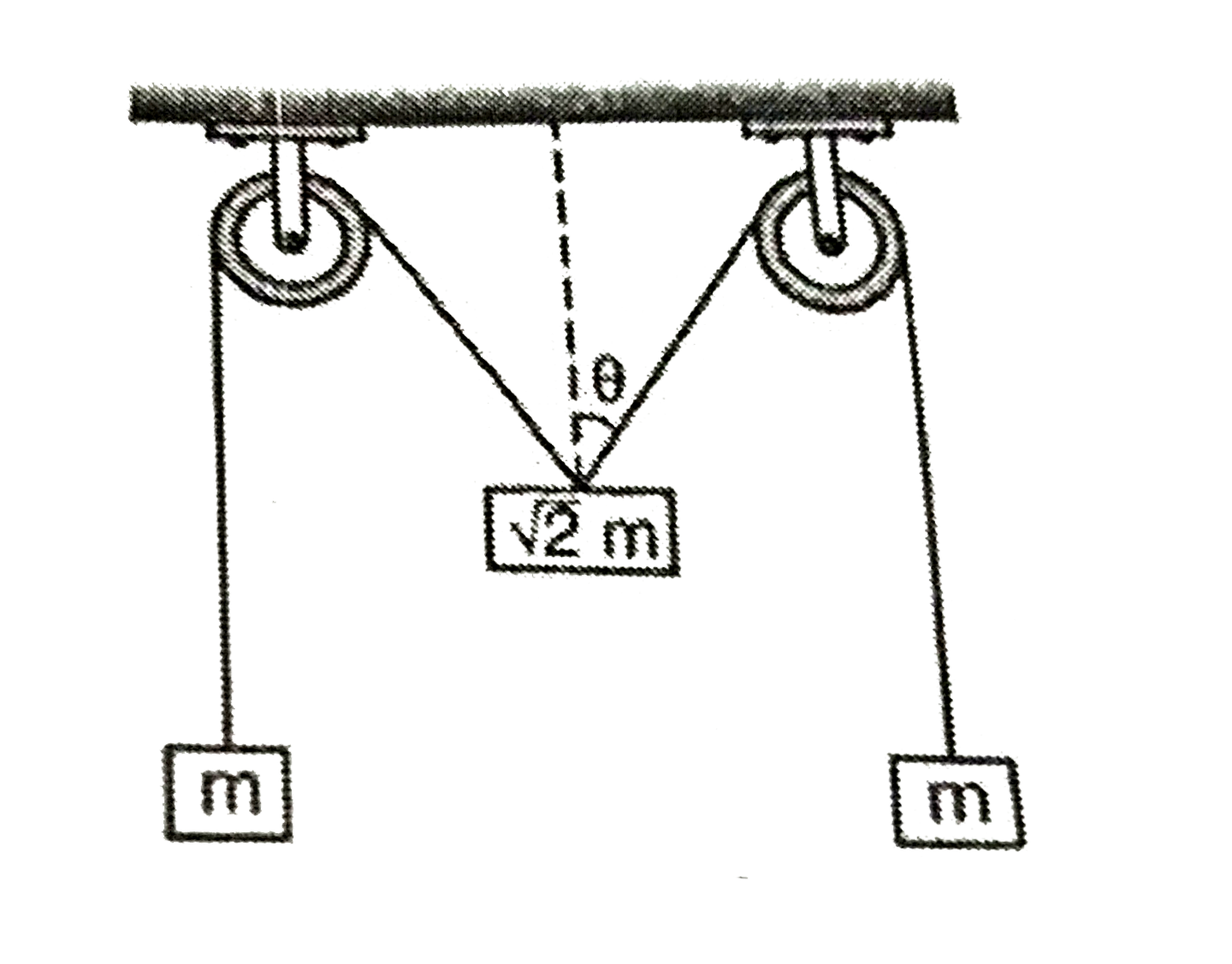
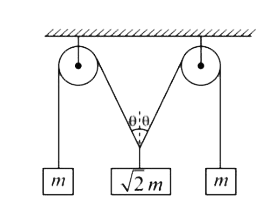
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle θ should be
0∘
30∘
45∘
60∘
The correct Answer is:c
For equilibrium in vertical direction for body B we have

√2mg=2Tcosθ
=2(mg)cosθ
T=mg(at equilibrium )
∴Cosθ=1√2⇒θ=45∘
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple correct answer type3videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Assertion -reasoning2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False4videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
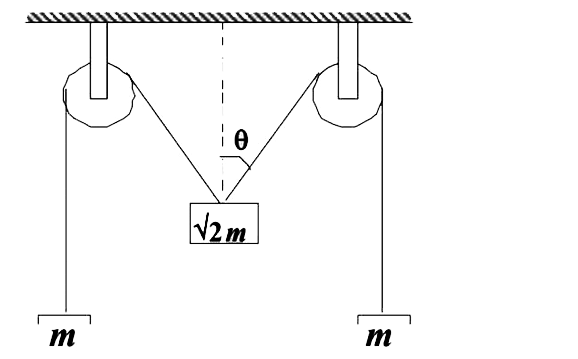
The pulley and strings shown in fig 15.3.16 are smooth and of negligible mass. For the system to remiain in equilibrium the angle θ should be
 AzeroB30∘C45∘D60∘
AzeroB30∘C45∘D60∘
The pulley and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle θ should be:
 View Solution
View SolutionA smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?
 View Solution
View SolutionFor the system shown in figure , to be in equilibrium , determine mass m .
 View Solution
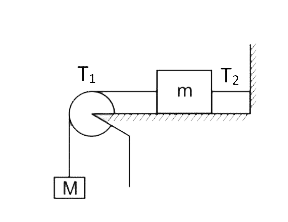
View SolutionFor the system shown in figure, the tensions in the string
 View Solution
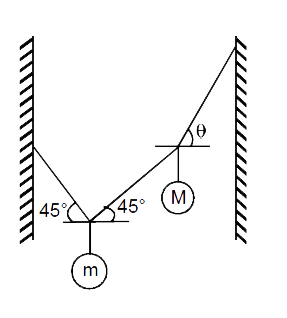
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
 View Solution
View SolutionFor the equilibrium of the system shown, the value of mass m should be
 View Solution
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
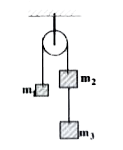
The tension in the string between masses m2andm3 isView Solution