Two masses each equal to m are lying on x-axis at (−a,0)(+a,0) respectively as shown in figure They are connected by a light string A force F is applied at the origin along vertical direction As a result the masses move toward each other without loosing contact with ground What is the acceleration of each mass? Assume the instantanceous position of the masses as(−x,0)and (x,0)
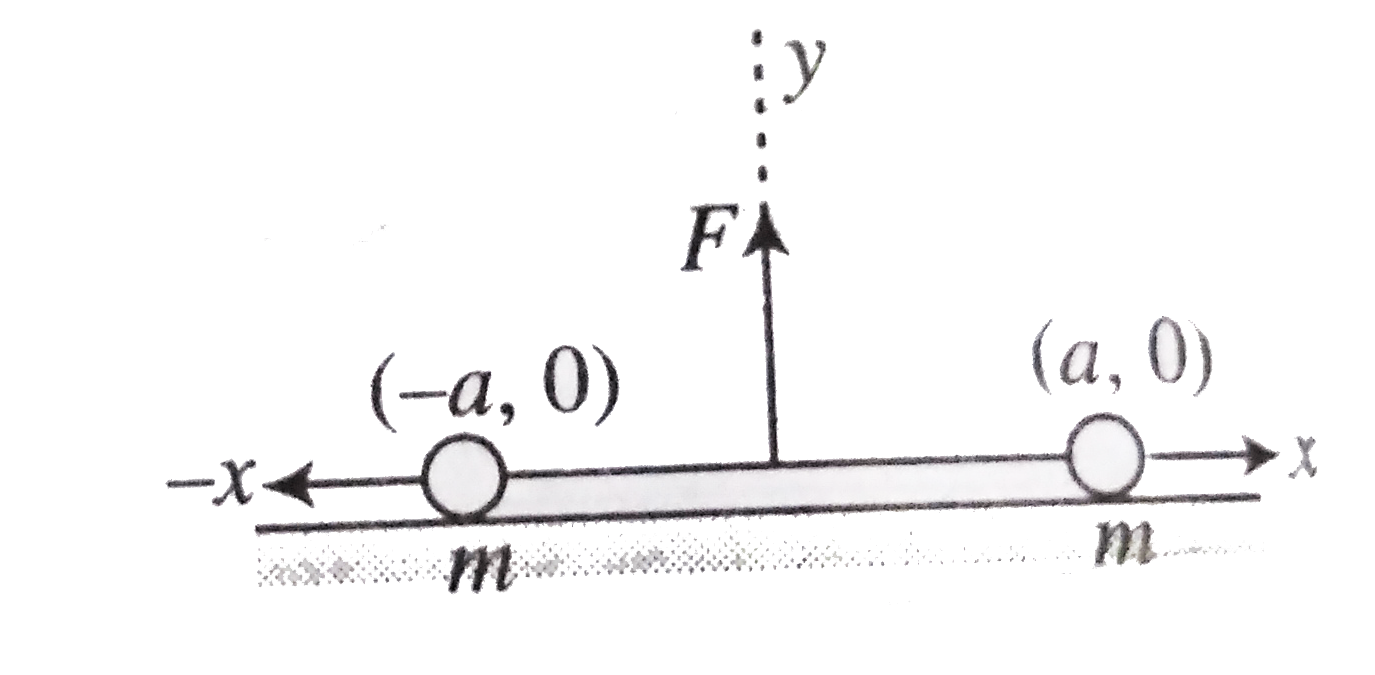
a. 2Fm√a2−x2x
b. 2Fm.x√a2−x2
c, F2m.x√a2−x2
d. Fmx√a2−x2
The correct Answer is:c
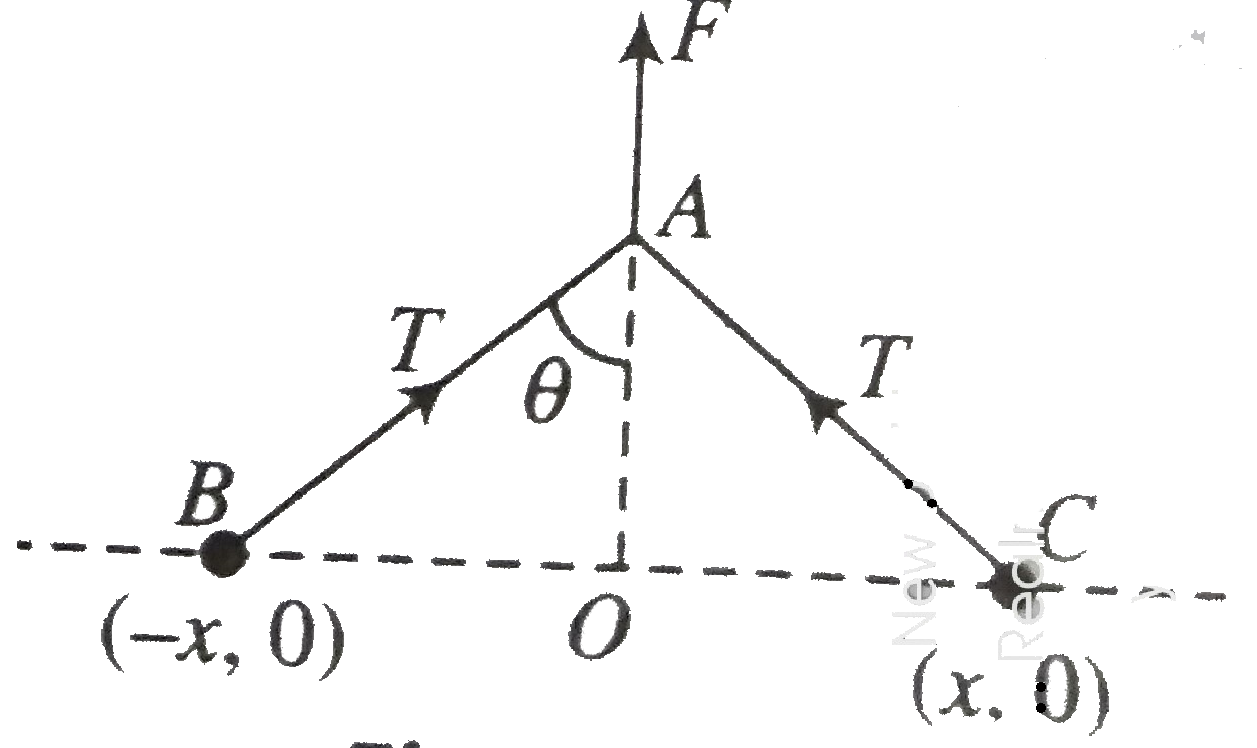
From figure F=2Tcosθ
T=F/2cosθ
The force responsible for motion of masses m x-axis is Tsinθ
ma=Tsinθ=F2sinθ×sinθ
=F2tanθ=F2×OBOA=F2×x√(a2−x2)
So a=F2m=x√a2−x2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple correct answer type3videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Assertion -reasoning2videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False4videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
Two masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is
 View Solution
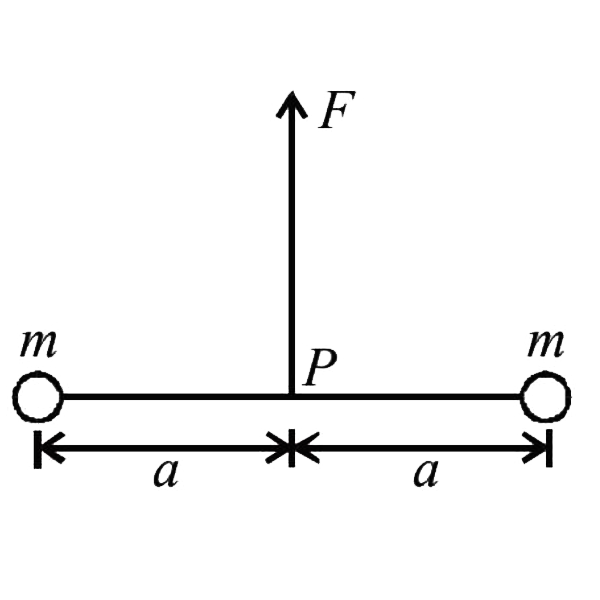
View SolutionTwo particles of mass m each are tied at the ends of a light string of length 2a. The whole system is kept on a frictionless horizontal surface with the string held tight so that each mass is at a distance a from the centre P (as shown in the figure). Now, the mid-point of the string is pulled vertically upwards with a small but constant force F. As a result, the particles move towards each other on the surface. The magnitude of acceleration, when the separation between them becomes 2x, is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.
 AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
AF2ma√a2−x2BF2m−x√a2−x2CF2mxaDF2m√a2−x2x
Three blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt
 View Solution
View SolutionThree blocks with masses m , 2m and 3m are connected by strings, as shown in the figure. After an upward force F is applied on block m , the masses move upward at costant speed v . What is the net force on the block of mass 2m ? (g is the acceleration due to gravity). ltBrgt
 View Solution
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
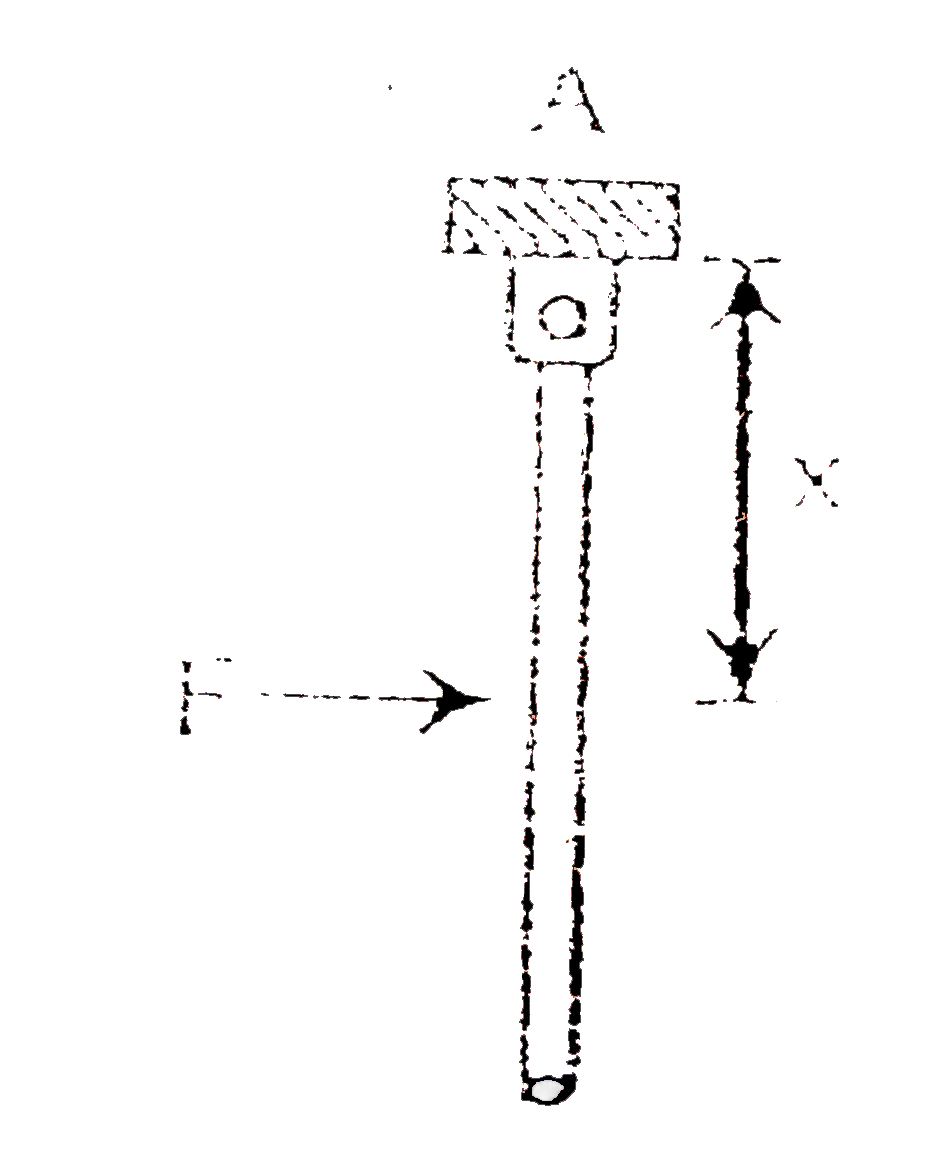 View Solution
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
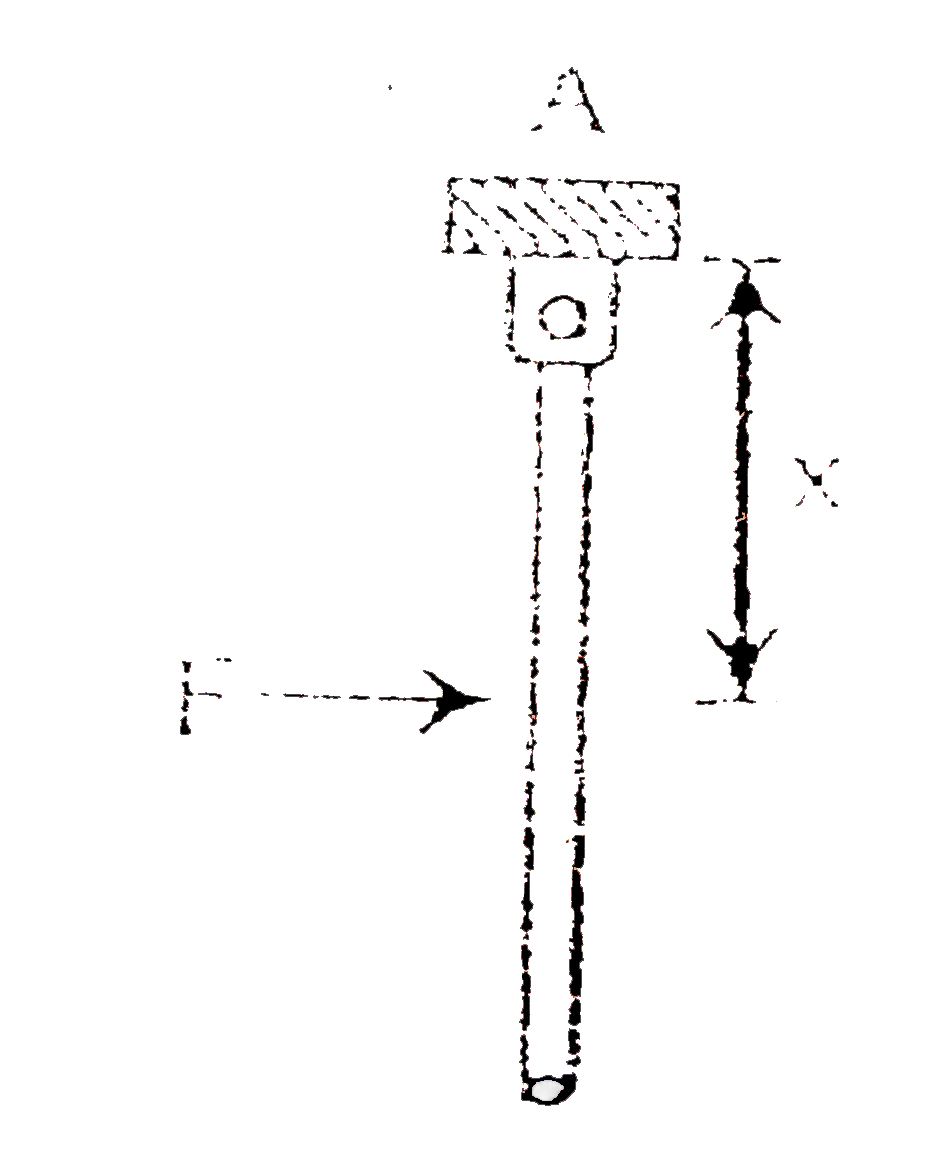 View Solution
View SolutionTwo blocks of masses M and 2M are connected to each other through a light spring as shown in figure . If we push the mass M with a force F which cause acceleration a in mass M. what will the acceleration in 2M?
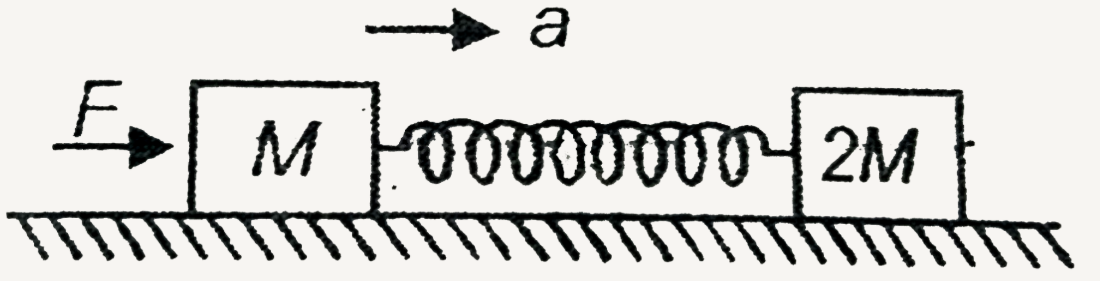 View Solution
View SolutionTwo charges, each equal to q, aer kept at x=−a and x=a on the x-axis. A particle of mass m and charge q0=q2 is placed at the origin. If charge q0 is given a small displacement (ylt lt a) along the y-axis, the net force acting on the particle is proportional to
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as
 View Solution
View Solution

