A block m1 strikes a stationary block m3 inelastically. Another block m2 is kept on m3. Neglecting the friction between all contacting surfaces, calculate the fractional decrease in KE of the system in collision.
To solve the problem of the inelastic collision between the blocks, we will follow these steps:
Step 1: Understand the System
We have three blocks:
- Block m1 is moving with an initial velocity v.
- Block m2 is resting on block m3, which is stationary.
- Block m3 is initially at rest.
Step 2: Apply Conservation of Momentum
Since the collision between m1 and m3 is inelastic, they will stick together after the collision. The momentum before the collision must equal the momentum after the collision.
Before the collision:
- Momentum of m1 = m1v
- Momentum of m2 = 0
- Momentum of m3 = 0
Total initial momentum = m1v
After the collision, let the combined mass of m1 and m3 move with a velocity V:
- Total mass after collision = m1+m3
- Total momentum after collision = (m1+m3)V
Setting the initial momentum equal to the final momentum:
m1v=(m1+m3)V
From this, we can solve for V:
V=m1vm1+m3
Step 3: Calculate Initial Kinetic Energy
The initial kinetic energy (KE) of the system is only due to block m1:
KEinitial=12m1v2
Step 4: Calculate Final Kinetic Energy
After the collision, the kinetic energy of the combined mass (m1+m3) moving with velocity V is:
KEfinal=12(m1+m3)V2
Substituting V from step 2:
KEfinal=12(m1+m3)(m1vm1+m3)2
=12(m1+m3)m21v2(m1+m3)2
=12m21v2m1+m3
Step 5: Calculate the Change in Kinetic Energy
The change in kinetic energy is given by:
ΔKE=KEinitial−KEfinal
Substituting the values:
ΔKE=12m1v2−12m21v2m1+m3
Factoring out 12v2:
ΔKE=12v2(m1−m21m1+m3)
Finding a common denominator:
=12v2(m1(m1+m3)−m21m1+m3)
=12v2(m1m3m1+m3)
Step 6: Calculate the Fractional Decrease in Kinetic Energy
The fractional decrease in kinetic energy is given by:
Fractional decrease=ΔKEKEinitial=12v2(m1m3m1+m3)12m1v2
Simplifying:
=m3m1+m3
Final Answer
The fractional decrease in kinetic energy of the system during the collision is:
m3m1+m3
We have three blocks:
- Block m1 is moving with an initial velocity v.
- Block m2 is resting on block m3, which is stationary.
- Block m3 is initially at rest.
Since the collision between m1 and m3 is inelastic, they will stick together after the collision. The momentum before the collision must equal the momentum after the collision.
- Momentum of m1 = m1v
- Momentum of m2 = 0
- Momentum of m3 = 0
- Total mass after collision = m1+m3
- Total momentum after collision = (m1+m3)V
m1v=(m1+m3)V
V=m1vm1+m3
The initial kinetic energy (KE) of the system is only due to block m1:
KEinitial=12m1v2
After the collision, the kinetic energy of the combined mass (m1+m3) moving with velocity V is:
KEfinal=12(m1+m3)V2
Substituting V from step 2:
KEfinal=12(m1+m3)(m1vm1+m3)2
=12(m1+m3)m21v2(m1+m3)2
=12m21v2m1+m3
The change in kinetic energy is given by:
ΔKE=KEinitial−KEfinal
Substituting the values:
ΔKE=12m1v2−12m21v2m1+m3
Factoring out 12v2:
ΔKE=12v2(m1−m21m1+m3)
Finding a common denominator:
=12v2(m1(m1+m3)−m21m1+m3)
=12v2(m1m3m1+m3)
The fractional decrease in kinetic energy is given by:
Fractional decrease=ΔKEKEinitial=12v2(m1m3m1+m3)12m1v2
Simplifying:
=m3m1+m3
The fractional decrease in kinetic energy of the system during the collision is:
m3m1+m3
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
In fig two block of mass mAandmB are rotating at radius r kept on a rough table consider friction (μ) between all the contact surface pulley is frictionless determine the angular speed of the turn table for which the blocks just begin to slide

View SolutionTwo blocks of masses m1 and m2 inter connected by a spring of stiffness k are placed on a horizontal surface. If a constant horizontal force F acts on the block m1 it slides through a distance x whereas m2 remains stationary. If the coefficient of friction between all contacting surfaces is μ, find the speed of the block m1 as the function x.

View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
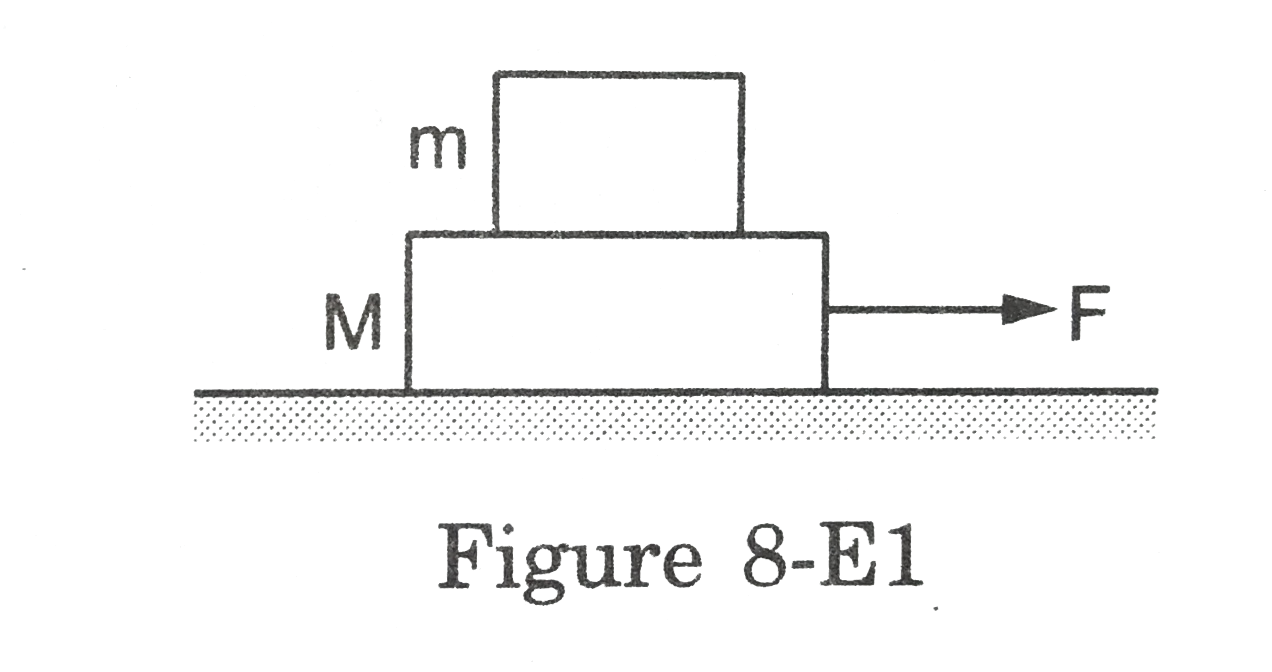
View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
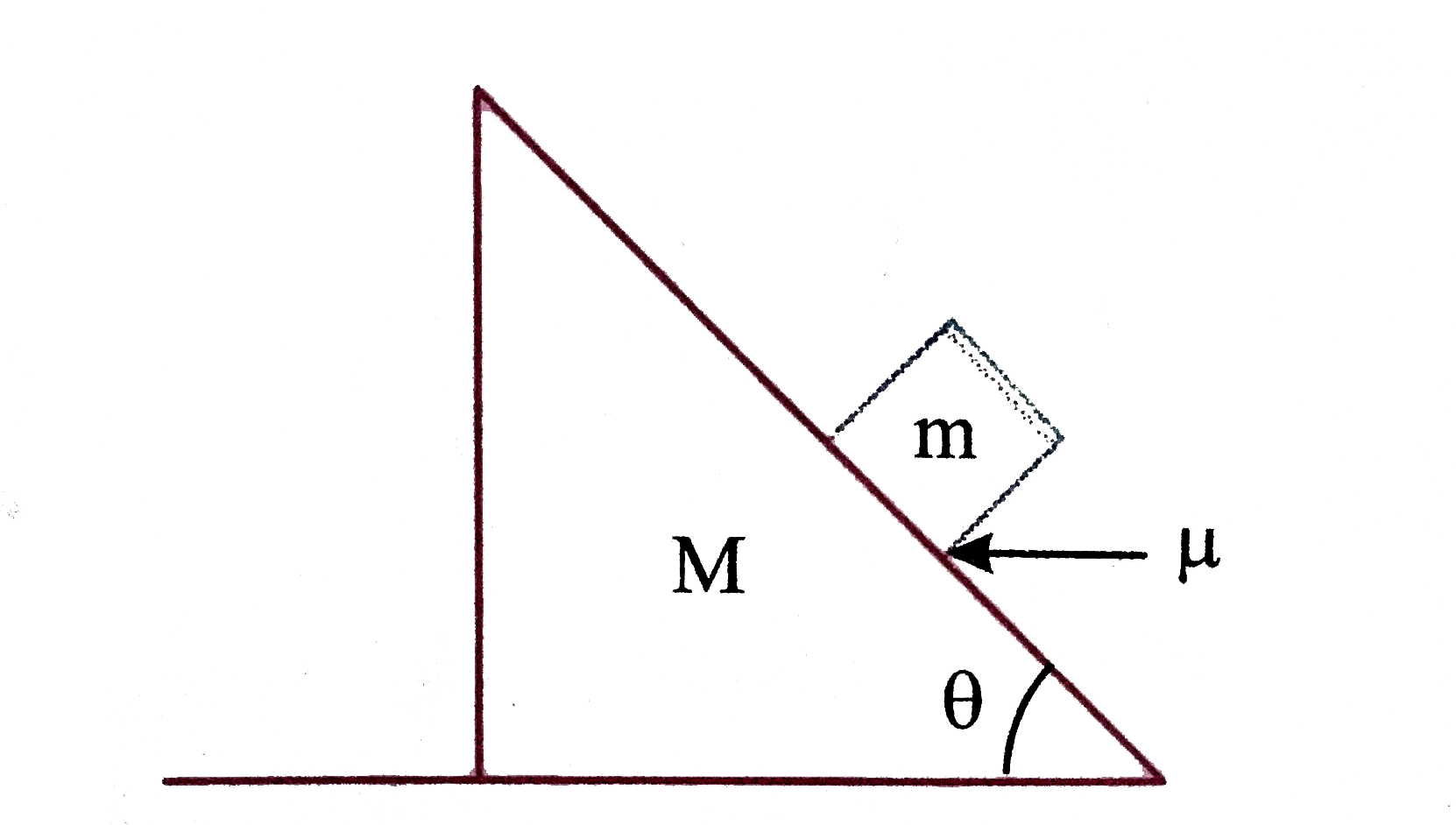
View SolutionCalculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
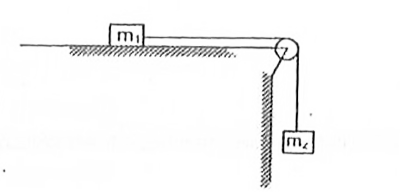
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionConsider three blocks placed one over the other as shown in Fig. Let as now pull the blocks with the force of magnitudes 18N,100N and 15N Take m1=m2=m3=10kg If the coefficient of static and kinetic friction between all contacting surface are μg=0.2 respectively find the

(a) Acceleration of the block s
(b) Friction at each surface
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA small block B of mass m2 is placed on another block A of mass m1 A constant horizontal force F is applied to the block A. All the surfaces are assumed to be frictionless. Find the acceleration of center of mass of the system
View Solution
