A man standing on a trolley pushes another identical a trolley (both trolleys are at rest on a rough surface), are set in motion and stop alter some time so that they If the ratio of mass of first trolley with man to mass of second trolley is 3, then find the ratio of the stopping distances of the second trolley to that of the first trolley. (Assume coefficient of friction to be the same for both the trolleys)
The correct Answer is:9
To solve the problem, we will follow these steps:
Step 1: Define the masses
Let the mass of the second trolley be M. According to the problem, the mass of the first trolley with the man is 3M.
Step 2: Apply the conservation of momentum
When the man pushes the second trolley, the momentum before and after must be conserved. Initially, both trolleys are at rest, so the total initial momentum is zero. After the push, let v1 be the velocity of the first trolley (with the man) and v2 be the velocity of the second trolley.
Using conservation of momentum:
(3M)v1+(M)v2=0
This implies:
3Mv1+Mv2=0⟹v2=−3v1
(Note: The negative sign indicates that the trolleys move in opposite directions.)
Step 3: Calculate the stopping distances
The stopping distance for an object under uniform deceleration can be calculated using the equation:
v2=u2+2as
Where:
- v is the final velocity (0 when stopping),
- u is the initial velocity,
- a is the acceleration (deceleration in this case),
- s is the stopping distance.
Rearranging gives:
s=u22a
For the first trolley (with the man):
s1=v212a
For the second trolley:
s2=v222a
Step 4: Substitute for v2
From our earlier finding, v2=−3v1. Thus:
s2=(−3v1)22a=9v212a
Step 5: Find the ratio of stopping distances
Now we can find the ratio of the stopping distances:
s2s1=9v212av212a=9v21v21=9
Conclusion
The ratio of the stopping distances of the second trolley to that of the first trolley is:
s2s1=9
Let the mass of the second trolley be M. According to the problem, the mass of the first trolley with the man is 3M.
When the man pushes the second trolley, the momentum before and after must be conserved. Initially, both trolleys are at rest, so the total initial momentum is zero. After the push, let v1 be the velocity of the first trolley (with the man) and v2 be the velocity of the second trolley.
(3M)v1+(M)v2=0
This implies:
3Mv1+Mv2=0⟹v2=−3v1
(Note: The negative sign indicates that the trolleys move in opposite directions.)
The stopping distance for an object under uniform deceleration can be calculated using the equation:
v2=u2+2as
Where:
- v is the final velocity (0 when stopping),
- u is the initial velocity,
- a is the acceleration (deceleration in this case),
- s is the stopping distance.
s=u22a
s1=v212a
s2=v222a
From our earlier finding, v2=−3v1. Thus:
s2=(−3v1)22a=9v212a
Now we can find the ratio of the stopping distances:
s2s1=9v212av212a=9v21v21=9
The ratio of the stopping distances of the second trolley to that of the first trolley is:
s2s1=9
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Integer16videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Two bodies of masses 1 kg and 2 kg moving with same velocities are stopped by the same force. Then, the ratio of their stopping distances is
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionTwo light trollwys of masses m1 and m2(=3m1) are connected by a spring. The spring is compressed and bound by a cord. The cord is burnt through, the spring expands and the trolleys move off in opposite direction. Assume that the coefficient of friction is the same for both trollwys.
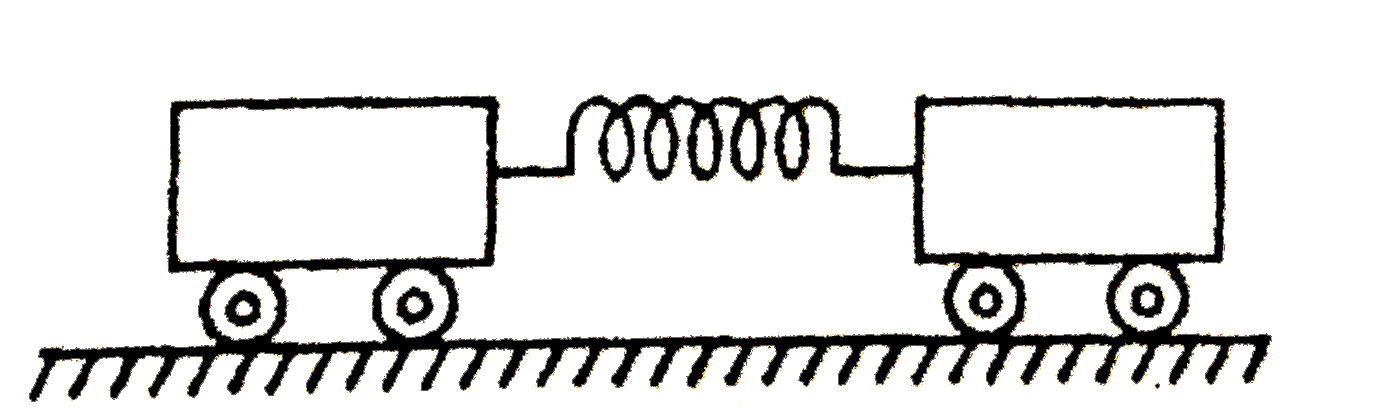 View Solution
View SolutionA sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
View SolutionA ball falls freely from rest. The ratio of the distance travelled in first, second, third and fourth second is
View SolutionA constant force F is applied on a trolley of initial mass m0 kept over a smooth surface. Sand is poured gently over the trolley at a constant rate of (μ)kg//s. Afer time t, find

(a) mass of the trolley (with sand)
(b) net force on the trolley
(c) velocity of trolleyView SolutionTwo trolleys of masses m and 3 m are connected by a spring. The spring is compressed and released the trolleys move off in opposite directions and come to rest after travelling distances s1, and s2, respectively. Assuming coefficient of friction is same for both the ratio of sto s1 to s2 is
View SolutionA man of mass m is standing at one end of a trolley of mass Mand length L placed at rest on a smooth horizontal surface. The man starts moving towards the other end and covers distance L, then distance moved by man w.r.t ground is
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution

