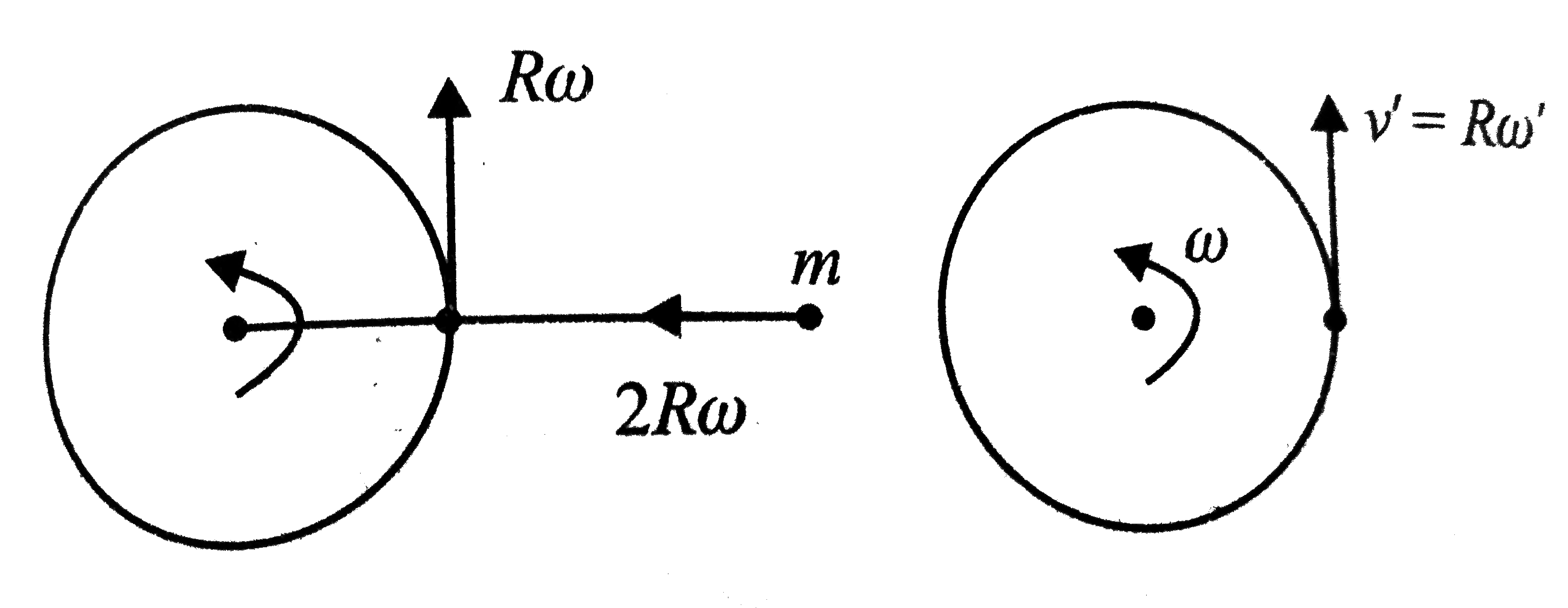
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
√173mωR
√353mωR
√373mωR
√293mωR
The correct Answer is:C
Apply conservation of angular momentum,
mR22ω=(mR22+mR2)ω'
ω'=ω3
|Pl|=2mRω
Impulse on particle= change in linear momentum
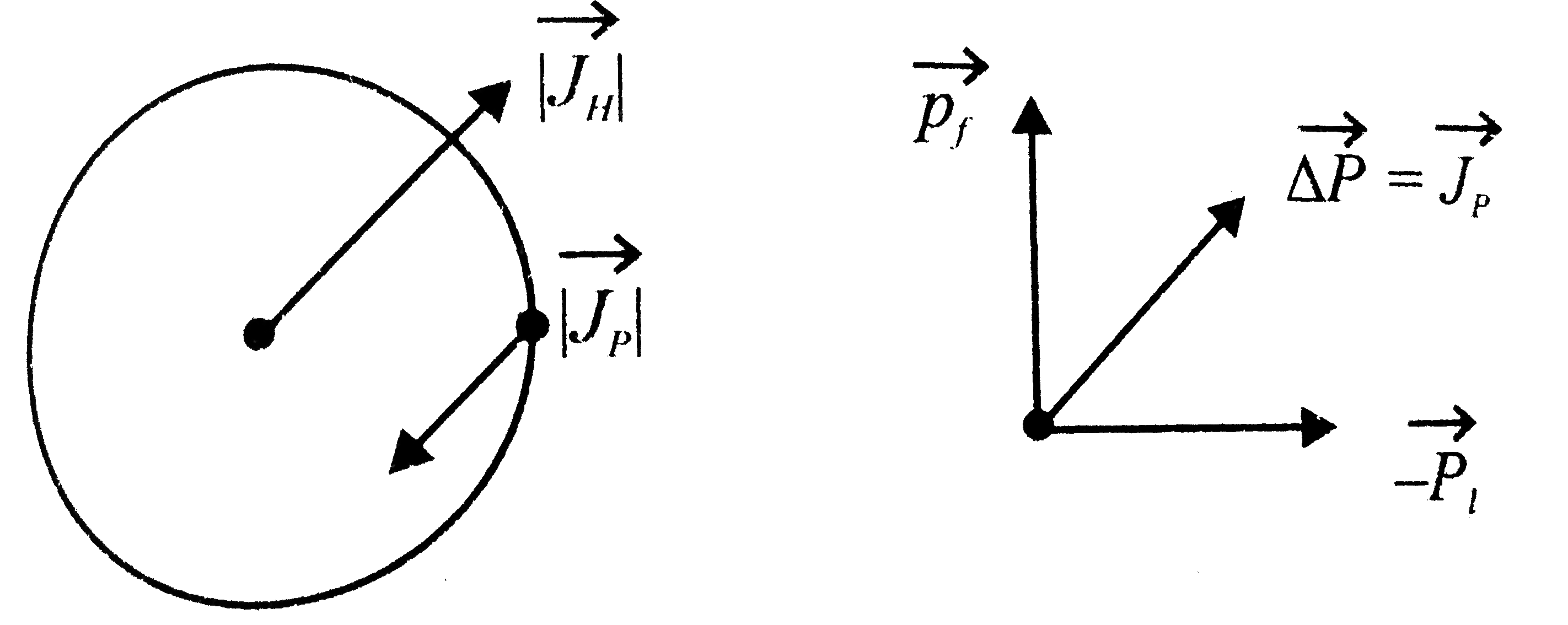
→J=△→p=→pj−→pi
|△→p|=√(mRω3)2+(2mrω)2=√373mRω
Impulse on hinge is negative of impulse on disc.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Fill In The Blanks
7 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionA nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity ω . The magnt moment of this disc is .
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. another disc of the same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is 2ω/√5.
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.
View Solution
