Two liquid jets coming out of the small holes at P and Q intersect at the point R. Find the position of R if We maintain the liquid level constant.
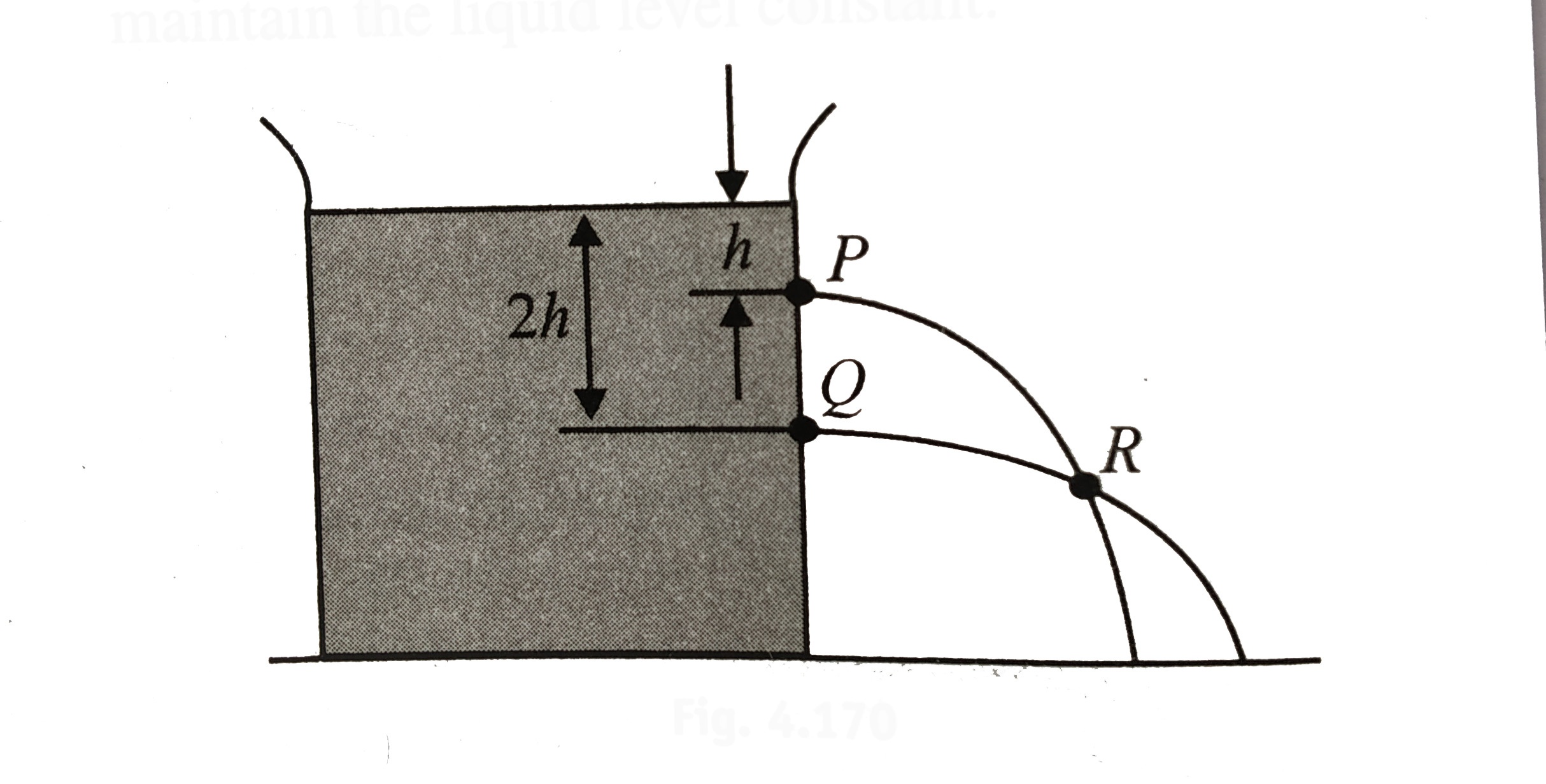
The correct Answer is:2√2h
Since y=gx2/2v2 for a horizontal projection for the same x we have y1,y2 and v1,v2.Putting y1−y2=h and other values find x and ys.
y1=gx22.2gh and y2=gx22.4gh
y1−y2=h=gx28gh⇒x=2√2h
and y2=g(8h2)2.4.gh⇒y2=h

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.410videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
The velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is
 View Solution
View SolutionThe velocity of the liquid coming out of a small hole of a vessel containing two different liquids of densities 2ρ and ρ as shown in the figure is
 View Solution
View SolutionLines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View SolutionLines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View SolutionLiquid is filled vessel of height 2H3. At the bottom of the vessel there is a spot P and a hole from which liquid is coming out. Let d be the distance of image of P from an eye at height H from bottom at an instant when level of liquid in vessel is x. If we plot a graph between d and x it be like
 View Solution
View SolutionA variable plane at constant distance p form the origin meets the coordinate axes at P,Q, and R. Find the locus of the point of intersection of planes drawn through P,Q, r and parallel to the coordinate planes.
View Solution_E01_218_Q01.png)
A large tank is filled with two liquids of specific gravities 2σ and σ. Two holes are made on the wall of the tank as shown. Find the ratio of the distance from O of the points on the ground where the jets from holes A & B strike.View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
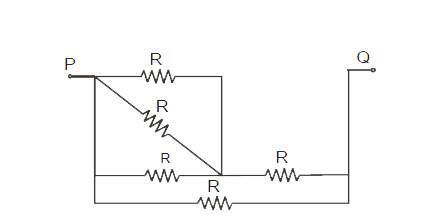
View SolutionThe equivalent resistance between the terminal point P and Q is 4Ω in the given circuit, then find out the resistance of R in ohms
 View Solution
View Solution

