A spaceship approaches the Moon (mass and radius along a parabolic path which is almost tangential to its surface. At the moment of the maximum approach, the brake rocket is fired to convert the spaceship into a satellite of the Moon. Find the change in speed.
The correct Answer is:
To solve the problem of finding the change in speed of a spaceship that approaches the Moon and then becomes a satellite, we can follow these steps:
Step 1: Understand the Initial Conditions
The spaceship is initially moving along a parabolic path, which means it is at the escape velocity from the Moon. The escape velocity ve from the Moon is given by the formula:
ve=√2GMR
where G is the universal gravitational constant, M is the mass of the Moon, and R is the radius of the Moon.
Step 2: Determine the Final Conditions
When the spaceship fires its brake rocket, it converts into a satellite of the Moon. The orbital velocity vo for a circular orbit around the Moon is given by:
vo=√GMR
Step 3: Calculate the Change in Speed
The change in speed Δv is the difference between the initial speed (escape velocity) and the final speed (orbital velocity):
Δv=vo−ve
Substituting the expressions for vo and ve:
Δv=√GMR−√2GMR
Step 4: Factor Out Common Terms
We can factor out √GMR:
Δv=√GMR(1−√2)
Step 5: Simplify the Expression
We know that √2≈1.414, so:
1−√2≈1−1.414=−0.414
Thus, we can express the change in speed as:
Δv≈−0.414√GMR
Final Result
The change in speed required to convert the spaceship into a satellite of the Moon is:
Δv=√GMR(1−√2)
The spaceship is initially moving along a parabolic path, which means it is at the escape velocity from the Moon. The escape velocity ve from the Moon is given by the formula:
ve=√2GMR
where G is the universal gravitational constant, M is the mass of the Moon, and R is the radius of the Moon.
When the spaceship fires its brake rocket, it converts into a satellite of the Moon. The orbital velocity vo for a circular orbit around the Moon is given by:
vo=√GMR
The change in speed Δv is the difference between the initial speed (escape velocity) and the final speed (orbital velocity):
Δv=vo−ve
Substituting the expressions for vo and ve:
Δv=√GMR−√2GMR
We can factor out √GMR:
Δv=√GMR(1−√2)
We know that √2≈1.414, so:
1−√2≈1−1.414=−0.414
Thus, we can express the change in speed as:
Δv≈−0.414√GMR
The change in speed required to convert the spaceship into a satellite of the Moon is:
Δv=√GMR(1−√2)
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Single Correct
122 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.4
16 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
A spaceship approaches the Moon along a parabolic trajectory which is almost tangent to the Moon's surface. At the moment of the maximum approach the brake rocket was fired for a short time interval, and the spaceship was transferred into a circular orbit of a Moon satellic. Find how the spaceship velocity modulus increased in the process of braking.
View Solution
A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.
View Solution
Knowledge Check
Two stars each of mass M and radius R are approaching each other for a head-on collision. They start approaching each other when their separation is r>>R. If their speed at this separation are negligible, the speed v with which they collide would be
Av=√GM(1R−1r)Bv=√GM(12R−1r)Cv=√GM(1R+1r)Dv=√GM(12R+1r)
The moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
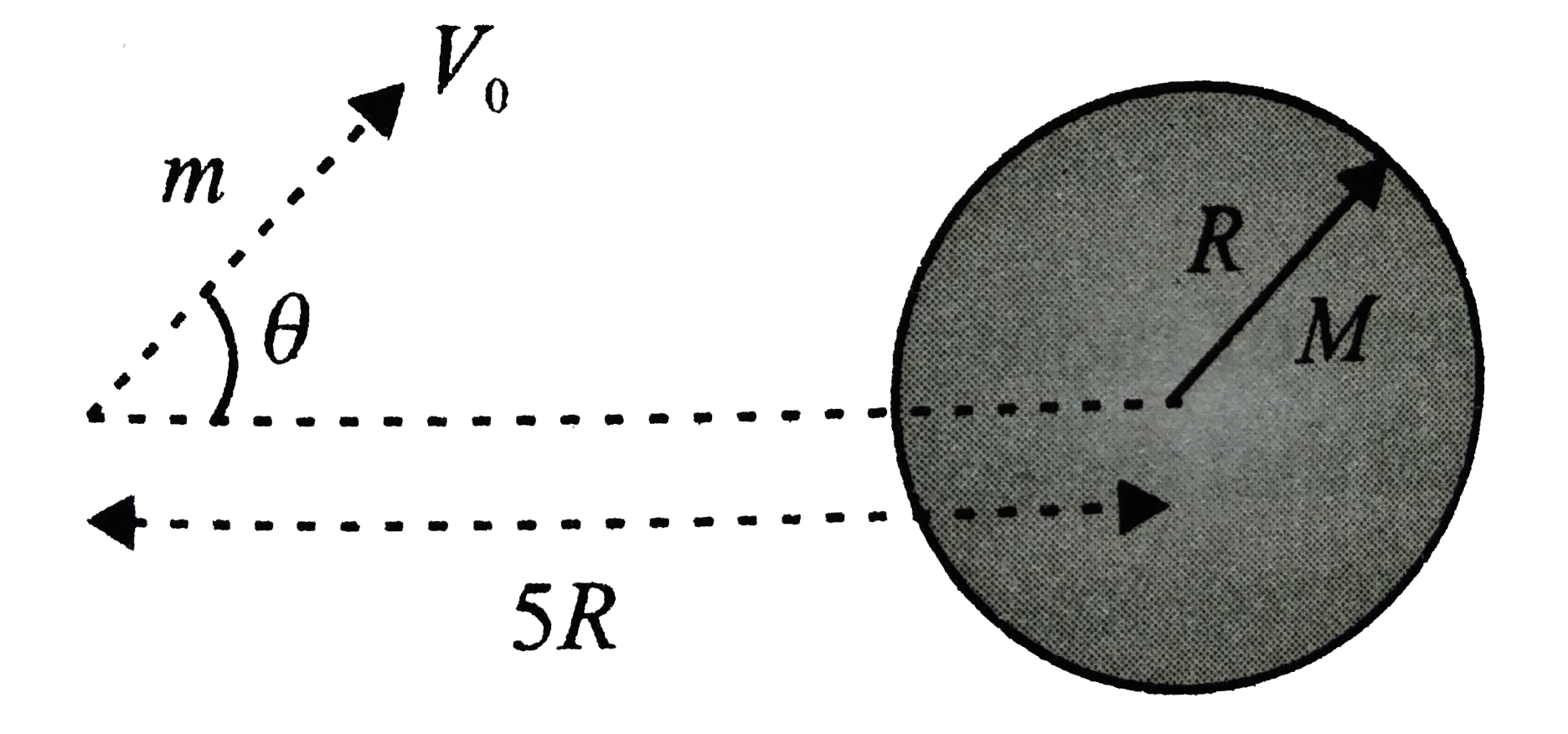
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?

View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionConsider the earth as a uniform sphere if mass M and radius R. Imagine a straight smooth tunnel made through the earth which connects any two points on its surface. Show that the motion of a particle of mass m along this tunnel under the action of gravitation would be simple harmonic. Hence, determine the time that a particle would take to go from one end to the other through the tunnel.
View Solution_E01_028_Q01.png)
Spacemen Fred's spaceship (which has negligible mass) is in an elliptical orbit about planet Bob. The minimum distance between the spaceship and the planet is R, the maximum distance between the spaceship and the planet is 2R. At the point of maximum distance, spaceman fred is traveling at speed v0. he then fires his thrusters so that he enters a circular orbit of radius 2R. what is his new speed?
View SolutionA small object of mass 'm' is moved over a rough, curved surface as shown. The force which moves it along the dotted path shown is always tangential to the curved path. If the object moves with negligible speed, find the work done by the force F in moving it from A to B. The coefficient of friction between the object and the curved surface is μ.

View Solution
