Two similarly and equally charged identical metal spheres A and B repel each other with a force of 2×10−5N. A third identical unchared sphere C is touched with A and then placed at the midpoint between A and B. Find the net electric force on C.
The correct Answer is:2×10−5 N toward sphere B
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Setup
We have two identical metal spheres A and B, both positively charged and repelling each other with a force of FAB=2×10−5N. A third identical uncharged sphere C is touched with sphere A and then placed at the midpoint between A and B.
Step 2: Determine the Charge Distribution
When sphere C is touched with sphere A, the charge from A will redistribute between A and C. Since both spheres A and C are identical, the charge on each will be half of the original charge Q on A. Thus, after touching:
- Charge on A: QA=Q2
- Charge on C: QC=Q2
Step 3: Define the Distances
Let the distance between spheres A and B be R. Since C is placed at the midpoint, the distances from C to A and C to B are both:
- Distance AC=R2
- Distance BC=R2
Step 4: Calculate the Forces on Sphere C
Using Coulomb's Law, we can calculate the forces acting on sphere C due to spheres A and B.
Force between A and C (F_CA):
FCA=kQA⋅QC(AC)2=k(Q2)(Q2)(R2)2=kQ24R24=kQ2R2
Force between B and C (F_CB):
Since sphere B retains the original charge Q:
FCB=kQB⋅QC(BC)2=kQ⋅(Q2)(R2)2=kQ22R24=2kQ2R2
Step 5: Determine the Net Force on Sphere C
The net force Fnet on sphere C is the difference between the forces due to spheres B and A:
Fnet=FCB−FCA=2kQ2R2−kQ2R2=kQ2R2
Step 6: Relate the Net Force to the Given Force
From the problem, we know that:
FAB=kQ2R2=2×10−5N
Thus, the net force on sphere C is:
Fnet=2×10−5N
Step 7: Conclusion
The net electric force on sphere C is directed away from sphere B, as FCB is greater than FCA.
Final Answer
The net electric force on sphere C is 2×10−5N directed away from sphere B.
---
We have two identical metal spheres A and B, both positively charged and repelling each other with a force of FAB=2×10−5N. A third identical uncharged sphere C is touched with sphere A and then placed at the midpoint between A and B.
When sphere C is touched with sphere A, the charge from A will redistribute between A and C. Since both spheres A and C are identical, the charge on each will be half of the original charge Q on A. Thus, after touching:
- Charge on A: QA=Q2
- Charge on C: QC=Q2
Let the distance between spheres A and B be R. Since C is placed at the midpoint, the distances from C to A and C to B are both:
- Distance AC=R2
- Distance BC=R2
Using Coulomb's Law, we can calculate the forces acting on sphere C due to spheres A and B.
FCA=kQA⋅QC(AC)2=k(Q2)(Q2)(R2)2=kQ24R24=kQ2R2
Since sphere B retains the original charge Q:
FCB=kQB⋅QC(BC)2=kQ⋅(Q2)(R2)2=kQ22R24=2kQ2R2
The net force Fnet on sphere C is the difference between the forces due to spheres B and A:
Fnet=FCB−FCA=2kQ2R2−kQ2R2=kQ2R2
From the problem, we know that:
FAB=kQ2R2=2×10−5N
Thus, the net force on sphere C is:
Fnet=2×10−5N
The net electric force on sphere C is directed away from sphere B, as FCB is greater than FCA.
The net electric force on sphere C is 2×10−5N directed away from sphere B.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two equally charged identical metal spheres X and Y repel each other with a force 5⋅10−4⋅ N another identical uncharged sphere C is touched to A and then placed at the mid-point between X and Y. Net electric force on C is
View SolutionTwo equally charged, indentical metal spheres A and B repel each other with a force F. The spheres are kept fixed with a distance r between them. A third identical, but uncharged sphere C is brought in contact with A and removed. The magnitude of the net electric force on A is
View Solution
Knowledge Check
Two point charges of +3μCand+4μC repel each other with a force of 10 N. If each is given an additional charge of −6μC, the new force is
A2 NB4 NC5 ND7.5 N
Two uniform spheres A (Hollow) and B (solid) of same radius R (√125GmPr, where P is _____
View SolutionTwo point charge +2C and +6C repel each other with a force of 12N . If a charge of −4C is given to each other of these charges , the force will now be
View SolutionTwo point charges +10 muC and +20 muC repel each other with a force of 100N. If a charge of-2 muC is added to each charge, then force between them will become
View SolutionTwo positive charges separated by a distance 2m repel each other with a force of 0.36N. If the combined charge is 26μC, the charges are
View SolutionTwo identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between them is F. A third identical conducting spheres, C,is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to :
View SolutionTwo identical conducting spheres 1 and 2 carry equal amounts of charge and are ficed apart at a certain distance larger than their diameters. The spheres repel each other with an electrical force of 88mN. A thired identical sphere 3, having an insulating handle and initially uncharged, is touched first to sphere 1 and then to sphere 2 and finally removed. Find the force between spheres 1 and 2 as shown if Figure.
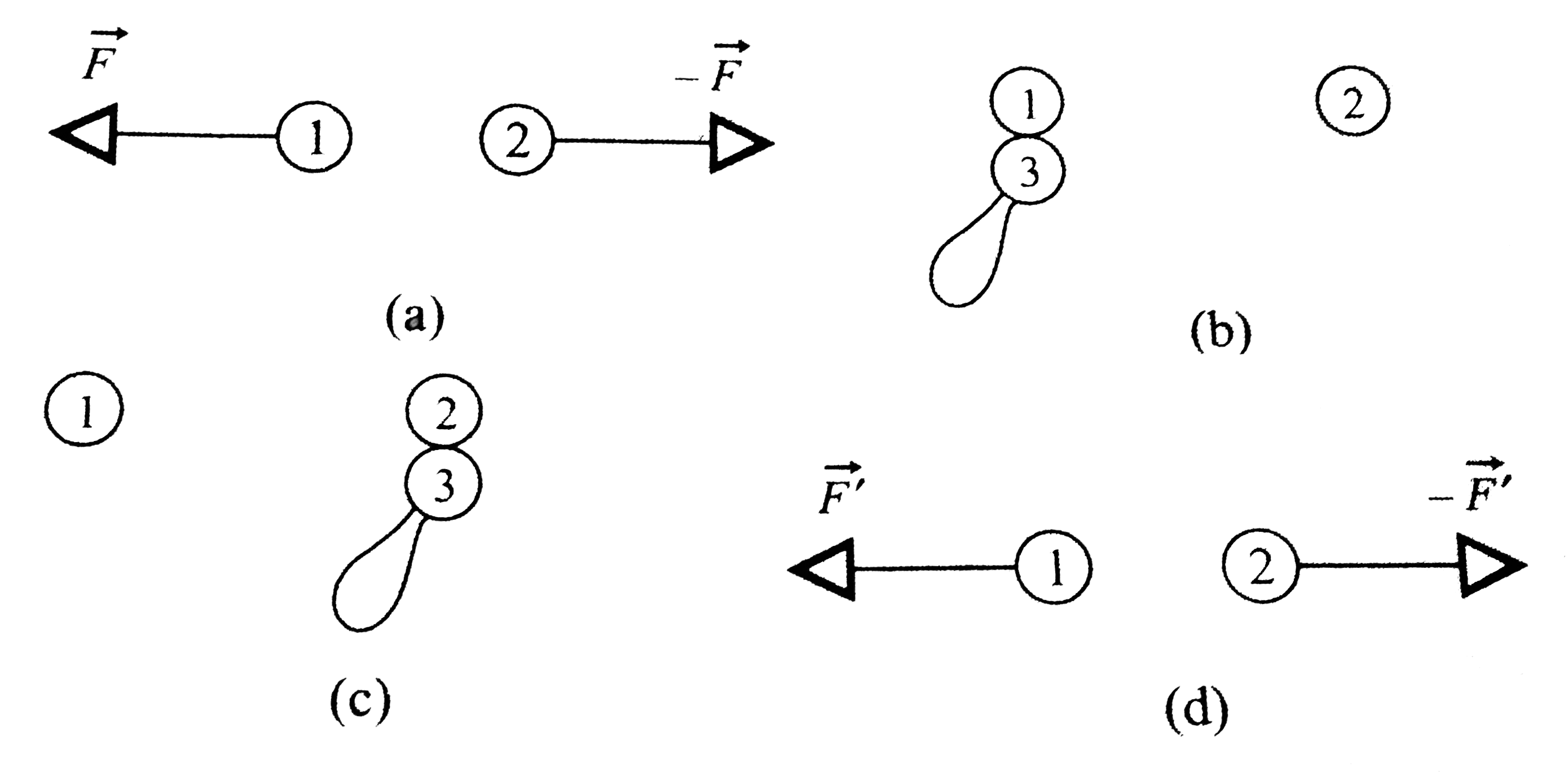 ,
,
View SolutionTwo point charges +2C and +6C repel each other with a force of 12N. If a charge q is given the each of the these charges then they attract with 4N. Then value q is
View Solution