A cube of side l has one corner at the origin of coordinates and extends along the positive Suppose that the electric field in this region is given by . Determine the charge inside the cube (a and b are some constants).
To determine the charge inside the cube given the electric field →E=(a+by)^j, we will use Gauss's law, which states:
ΦE=Qencϵ0
where ΦE is the electric flux through a closed surface, Qenc is the charge enclosed within that surface, and ϵ0 is the permittivity of free space.
1. Identify the Cube and Electric Field:
- The cube has a side length l and one corner at the origin, extending along the positive x, y, and z axes.
- The electric field is given as →E=(a+by)^j.
2. Determine the Relevant Surfaces:
- The cube has six faces, but only the faces that are perpendicular to the y-axis will contribute to the electric flux. These faces are located at y=0 and y=l.
3. Calculate the Electric Flux:
- The electric flux ΦE through a surface is given by the integral:
ΦE=∫→E⋅d→A
- For the face at y=l:
- The area vector d→A points in the ^j direction, and the area is l2.
- Thus, the electric field at this face is →E(y=l)=a+bl.
- Therefore, the flux through this face is:
ΦE,y=l=(a+bl)l2
- For the face at y=0:
- The electric field at this face is →E(y=0)=a+b(0)=a.
- The area vector d→A points in the negative ^j direction, so it is −l2^j.
- Therefore, the flux through this face is:
ΦE,y=0=a(−l2)=−al2
4. Total Electric Flux:
- The total electric flux ΦE through the cube is the sum of the fluxes through the two relevant faces:
ΦE=ΦE,y=l+ΦE,y=0=(a+bl)l2−al2
- Simplifying this gives:
ΦE=bl3
5. Apply Gauss's Law:
- According to Gauss's law:
ΦE=Qencϵ0
- Substituting the expression for ΦE:
bl3=Qencϵ0
6. Solve for the Enclosed Charge:
- Rearranging gives:
Qenc=bl3ϵ0
Final Answer:
The charge enclosed inside the cube is:
Qenc=bl3ϵ0
- The cube has a side length l and one corner at the origin, extending along the positive x, y, and z axes.
- The electric field is given as →E=(a+by)^j.
- The cube has six faces, but only the faces that are perpendicular to the y-axis will contribute to the electric flux. These faces are located at y=0 and y=l.
- The electric flux ΦE through a surface is given by the integral:
ΦE=∫→E⋅d→A
- For the face at y=l:
- The area vector d→A points in the ^j direction, and the area is l2.
- Thus, the electric field at this face is →E(y=l)=a+bl.
- Therefore, the flux through this face is:
ΦE,y=l=(a+bl)l2
- The electric field at this face is →E(y=0)=a+b(0)=a.
- The area vector d→A points in the negative ^j direction, so it is −l2^j.
- Therefore, the flux through this face is:
ΦE,y=0=a(−l2)=−al2
- The total electric flux ΦE through the cube is the sum of the fluxes through the two relevant faces:
ΦE=ΦE,y=l+ΦE,y=0=(a+bl)l2−al2
- Simplifying this gives:
ΦE=bl3
- According to Gauss's law:
ΦE=Qencϵ0
- Substituting the expression for ΦE:
bl3=Qencϵ0
- Rearranging gives:
Qenc=bl3ϵ0
The charge enclosed inside the cube is:
Qenc=bl3ϵ0
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Example
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.1
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
Electric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
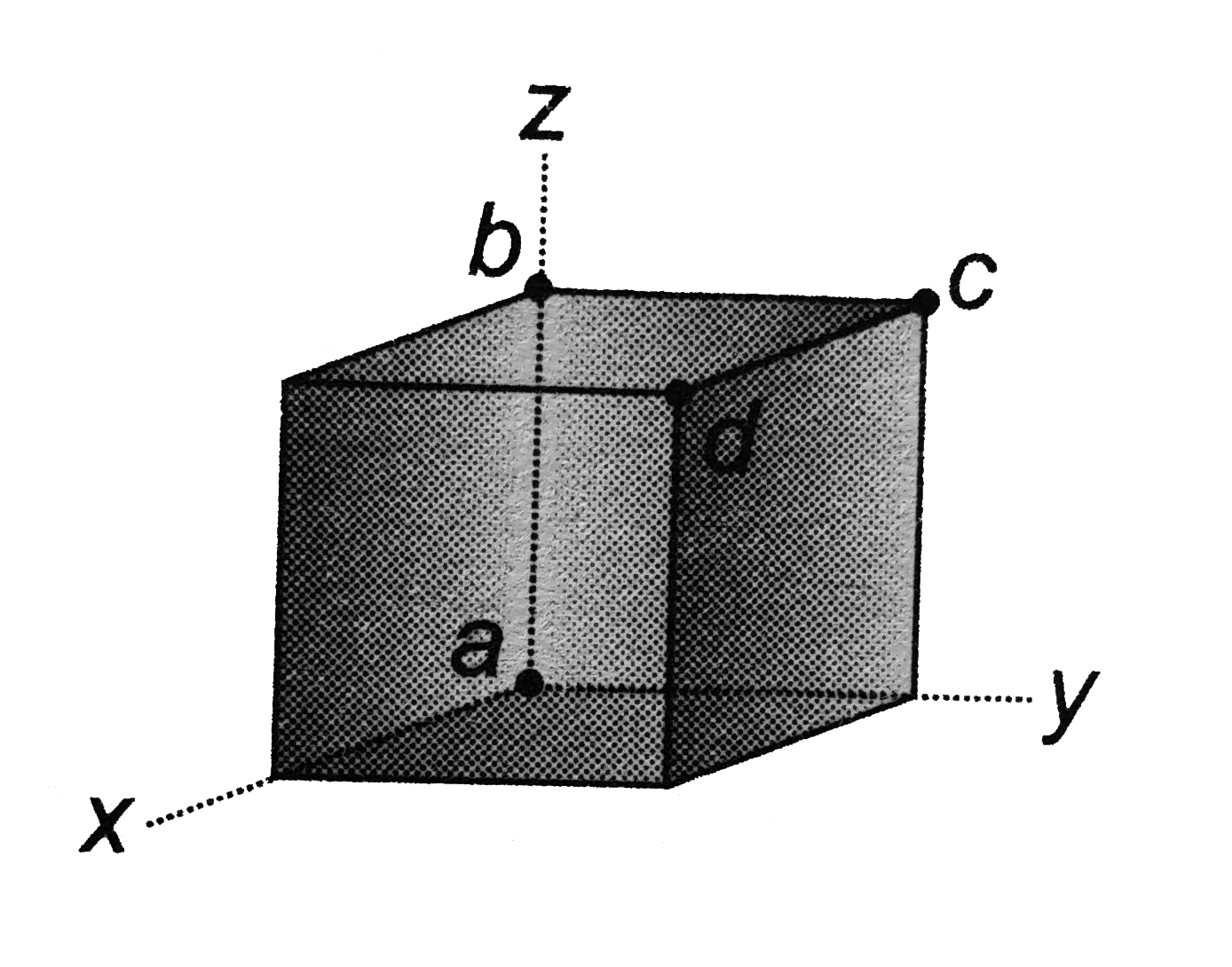
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
View SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
View SolutionA cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube is
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
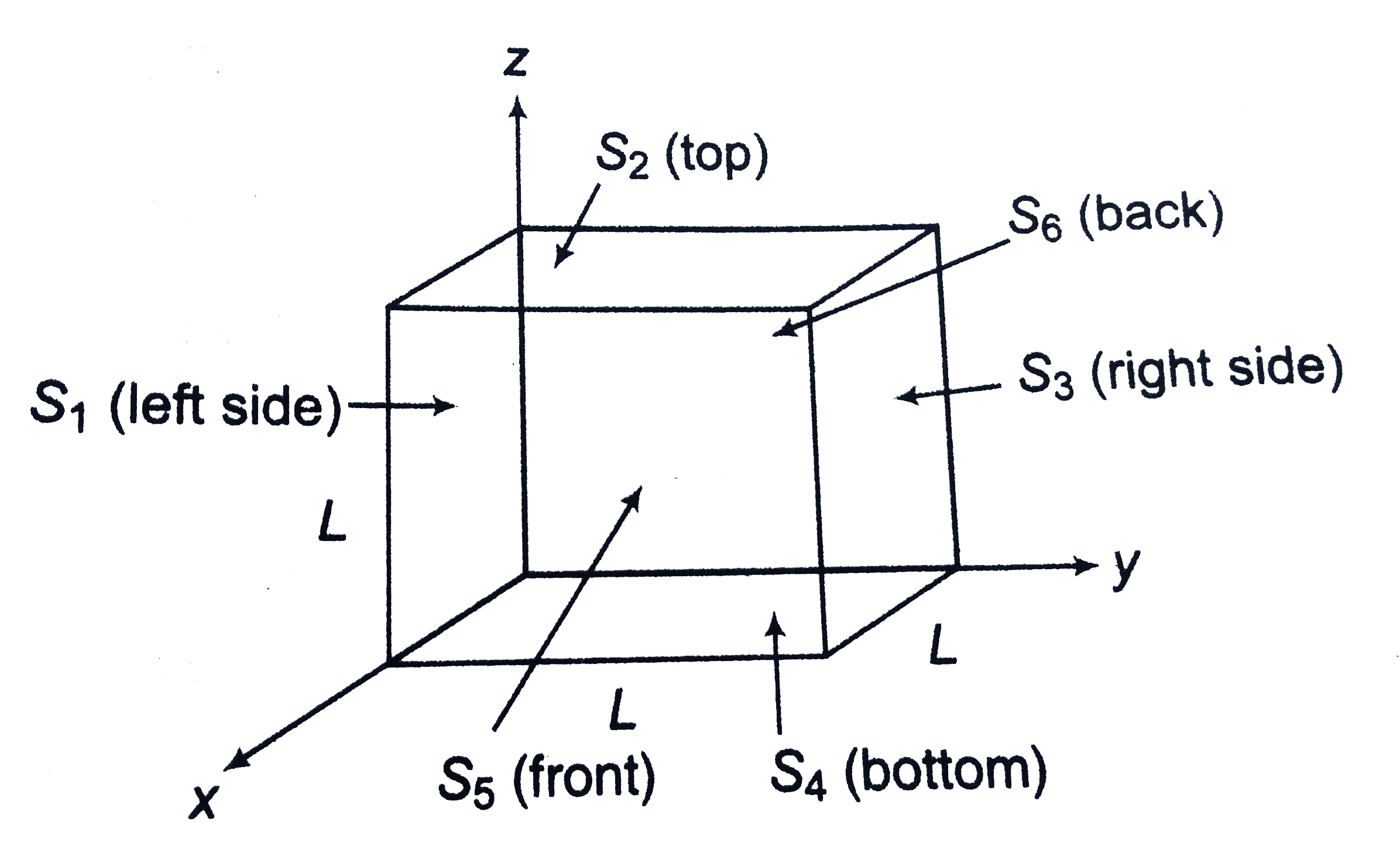
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.
View SolutionA positively charged particle is moving along the positive x-axis in a unifom electric field→E=E0ˆj and magnetic field →B=B0ˆk (where E0 and B0 are positive constants), then
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View Solution
