The surface density on a copper sphere is σ. The electric field strength on the surface of the sphere is
σ
σ/2
σ/2ε0
σ/ε0
The correct Answer is:D
To find the electric field strength on the surface of a copper sphere with a surface charge density σ, we can use Gauss's Law. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a copper sphere with a uniform surface charge density σ. We need to calculate the electric field strength E at the surface of the sphere.
Step 2: Apply Gauss's Law
Gauss's Law states that the electric flux ΦE through a closed surface is equal to the charge Qenc enclosed by that surface divided by the permittivity of free space ϵ0:
ΦE=Qencϵ0
Step 3: Choose a Gaussian Surface
For a sphere, we can choose a Gaussian surface that is also a sphere with the same radius as the copper sphere. The electric field E is uniform and radial at the surface of the sphere.
Step 4: Calculate the Electric Flux
The electric flux through the Gaussian surface is given by:
ΦE=E⋅A
where A is the surface area of the Gaussian sphere. The surface area A of a sphere is given by:
A=4πr2
where r is the radius of the sphere.
Step 5: Calculate the Enclosed Charge
The total charge Qenc enclosed by the Gaussian surface is given by the surface charge density multiplied by the surface area of the sphere:
Qenc=σ⋅A=σ⋅4πr2
Step 6: Substitute into Gauss's Law
Substituting the expressions for electric flux and enclosed charge into Gauss's Law:
E⋅(4πr2)=σ⋅(4πr2)ϵ0
Step 7: Simplify the Equation
We can cancel 4πr2 from both sides of the equation (assuming r≠0):
E=σϵ0
Conclusion
Thus, the electric field strength E on the surface of the copper sphere is:
E=σϵ0
We have a copper sphere with a uniform surface charge density σ. We need to calculate the electric field strength E at the surface of the sphere.
Gauss's Law states that the electric flux ΦE through a closed surface is equal to the charge Qenc enclosed by that surface divided by the permittivity of free space ϵ0:
ΦE=Qencϵ0
For a sphere, we can choose a Gaussian surface that is also a sphere with the same radius as the copper sphere. The electric field E is uniform and radial at the surface of the sphere.
The electric flux through the Gaussian surface is given by:
ΦE=E⋅A
where A is the surface area of the Gaussian sphere. The surface area A of a sphere is given by:
A=4πr2
where r is the radius of the sphere.
The total charge Qenc enclosed by the Gaussian surface is given by the surface charge density multiplied by the surface area of the sphere:
Qenc=σ⋅A=σ⋅4πr2
Substituting the expressions for electric flux and enclosed charge into Gauss's Law:
E⋅(4πr2)=σ⋅(4πr2)ϵ0
We can cancel 4πr2 from both sides of the equation (assuming r≠0):
E=σϵ0
Thus, the electric field strength E on the surface of the copper sphere is:
E=σϵ0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
A spherical charged conductor has surface density of charge as σ. The electric field intensity on its surface is E. If the radius of the surface is doubled, keeping σ uncharged, what will be the electric field intensity on the new sphere ?
View SolutionCharge density of the given surface is s. Then electric field stranght at the centre (of quarter sphere) is
 View Solution
View SolutionConsider two concentric conducting spheres. The outer sphere is hollow and initially has a charge −7Q on it. The inner sphere is solid and has a charge +2Q on it.
a. How much charge is on the outer surface and inner surface of the outer sphere.
b. If a wire is connected between the inner and outer sphere, after electrostatic equilibrium is established how much total charge is on the outer sphere? How much charge is on the outer surface and inner surface of the outer sphere? Does the electric field at the surface of the inside sphere change when the wire is connected?
c. We return to original condition in (a). We now connect the outer sphere to ground with a wire and then disconnect it. How much total charge will be on the outer sphere? How much charge will be on the inner surface and outer surface of the outer sphere?View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
 View Solution
View SolutionImagine a short diploe at the center of a spherical surface. If the magnitude of the electric field at a certain point on the surface of he sphere is 10NC_1 then which of the following cannot be the magnitude of the electric field anywhere on the surface of the sphere?
View SolutionEquipotential surfaces are shown in figure. Then the electric field strength will be
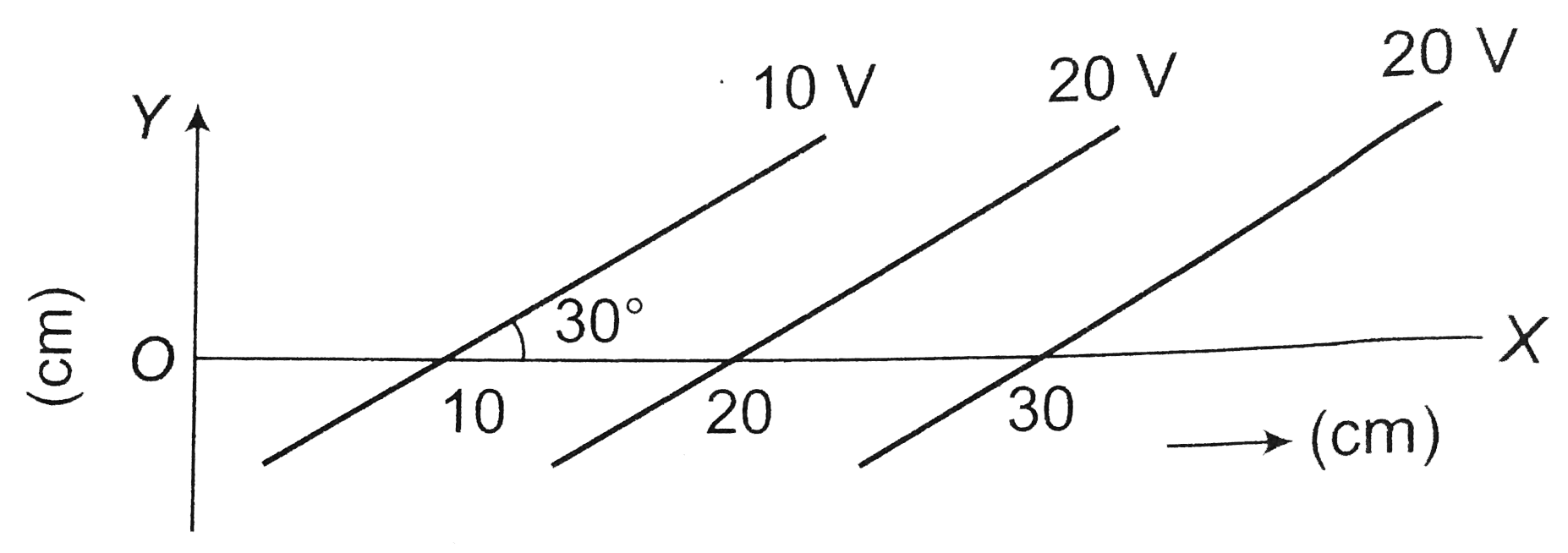 View Solution
View SolutionA spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V .Now radius of sphere is halved keeping the charge density as constant .The new electric field on the surface and potential at the centre of the sphere are
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionThe electric potential on the surface of a sphere of radius R and charge 3×10−6 C is 500 V The intensity of electric field on the surface of the sphere ( inNC−1) is
View Solution

