Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
−4
−32/25
32/25
4
To solve the problem, we need to find the ratio of the volume charge densities ρ1 and ρ2 of two non-conducting solid spheres of radii R and 2R respectively, given that the net electric field at a distance 2R from the center of the smaller sphere is zero.
1. Identify the Electric Fields:
- The electric field E1 due to the smaller sphere (radius R) at a distance 2R from its center can be calculated using the formula for the electric field outside a uniformly charged sphere:
E1=KQ1(2R)2
- The charge Q1 of the smaller sphere can be expressed in terms of its volume charge density ρ1:
Q1=ρ1⋅Volume of the sphere=ρ1⋅43πR3
- Substituting Q1 into the equation for E1:
E1=K(ρ1⋅43πR3)4R2=Kρ1⋅πR3
2. Electric Field from the Larger Sphere:
- The electric field E2 due to the larger sphere (radius 2R) at a distance 2R from the center of the smaller sphere can be calculated using the formula for the electric field inside a uniformly charged sphere:
E2=ρ2R3ϵ0
- Here, R is the radius of the smaller sphere, and ρ2 is the charge density of the larger sphere.
3. Set the Electric Fields Equal:
- Since the net electric field at the point 2R from the center of the smaller sphere is zero, we have:
E1=E2
- Substituting the expressions for E1 and E2:
Kρ1⋅πR3=ρ2R3ϵ0
4. Simplify the Equation:
- Cancel R and 13 from both sides:
Kρ1⋅π=ρ2ϵ0
5. Find the Ratio ρ1ρ2:
- Rearranging gives:
ρ1ρ2=1K⋅πϵ0
- Since K=14πϵ0:
ρ1ρ2=1(14πϵ0)⋅πϵ0=4ϵ201=4
Final Result:
The ratio ρ1ρ2 is 4:1.
- The electric field E1 due to the smaller sphere (radius R) at a distance 2R from its center can be calculated using the formula for the electric field outside a uniformly charged sphere:
E1=KQ1(2R)2
- The charge Q1 of the smaller sphere can be expressed in terms of its volume charge density ρ1:
Q1=ρ1⋅Volume of the sphere=ρ1⋅43πR3
- Substituting Q1 into the equation for E1:
E1=K(ρ1⋅43πR3)4R2=Kρ1⋅πR3
- The electric field E2 due to the larger sphere (radius 2R) at a distance 2R from the center of the smaller sphere can be calculated using the formula for the electric field inside a uniformly charged sphere:
E2=ρ2R3ϵ0
- Here, R is the radius of the smaller sphere, and ρ2 is the charge density of the larger sphere.
- Since the net electric field at the point 2R from the center of the smaller sphere is zero, we have:
E1=E2
- Substituting the expressions for E1 and E2:
Kρ1⋅πR3=ρ2R3ϵ0
- Cancel R and 13 from both sides:
Kρ1⋅π=ρ2ϵ0
- Rearranging gives:
ρ1ρ2=1K⋅πϵ0
- Since K=14πϵ0:
ρ1ρ2=1(14πϵ0)⋅πϵ0=4ϵ201=4
The ratio ρ1ρ2 is 4:1.
Similar Questions
A non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
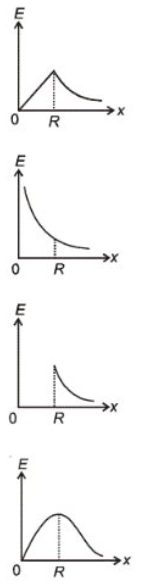 View Solution
View SolutionTwo non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region
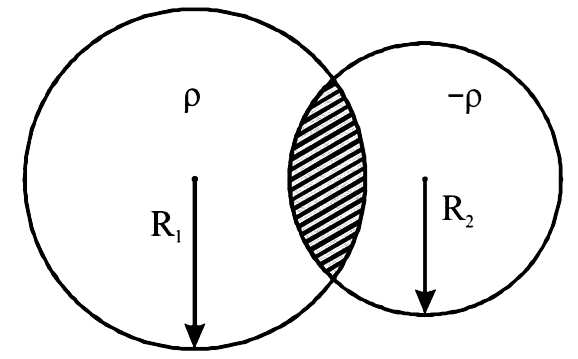 View Solution
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionA nonconducting sphere of radius R is filled with uniform volume charge density −ρ. The center of this sphere is displaced from the origin by →d. The electric field →E at any point P having position vector inside the sphere is
 View Solution
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View Solution

