Two long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
The correct Answer is:C
To find the current per unit length flowing from one coaxial conducting cylinder to another, we can follow these steps:
Step 1: Understand the Setup
We have two long coaxial conducting cylinders with inner radius a and outer radius b. They are separated by a material with conductivity σ, and a constant potential difference V is maintained between them.
Step 2: Consider a Differential Element
To analyze the current flow, we can consider a thin cylindrical shell of radius x and thickness dx between the two cylinders. The length of the cylinder is L.
Step 3: Calculate the Resistance of the Differential Element
The resistance dR of the differential element can be expressed as:
dR=dxσ⋅A
where A is the cross-sectional area through which the current flows. For a cylindrical shell, the area A is given by:
A=2πxL
Thus, the resistance becomes:
dR=dxσ⋅(2πxL)=12πσL⋅dxx
Step 4: Integrate to Find Total Resistance
To find the total resistance R between the two cylinders, we integrate dR from a to b:
R=∫badR=∫ba12πσL⋅dxx
This integral evaluates to:
R=12πσL(lnx)ba=12πσL(lnb−lna)=12πσLlnba
Step 5: Use Ohm's Law to Find Current
According to Ohm's Law, the current I flowing through the resistance R with a potential difference V is given by:
I=VR
Substituting the expression for R:
I=V⋅⎛⎝2πσLlnba⎞⎠
Step 6: Find Current per Unit Length
To find the current per unit length I′, we divide the total current I by the length L:
I′=IL=V⋅2πσlnba
Final Answer
Thus, the current per unit length flowing from one cylinder to the other is:
I′=2πσVlnba
We have two long coaxial conducting cylinders with inner radius a and outer radius b. They are separated by a material with conductivity σ, and a constant potential difference V is maintained between them.
To analyze the current flow, we can consider a thin cylindrical shell of radius x and thickness dx between the two cylinders. The length of the cylinder is L.
The resistance dR of the differential element can be expressed as:
dR=dxσ⋅A
where A is the cross-sectional area through which the current flows. For a cylindrical shell, the area A is given by:
A=2πxL
Thus, the resistance becomes:
dR=dxσ⋅(2πxL)=12πσL⋅dxx
To find the total resistance R between the two cylinders, we integrate dR from a to b:
R=∫badR=∫ba12πσL⋅dxx
This integral evaluates to:
R=12πσL(lnx)ba=12πσL(lnb−lna)=12πσLlnba
According to Ohm's Law, the current I flowing through the resistance R with a potential difference V is given by:
I=VR
Substituting the expression for R:
I=V⋅⎛⎝2πσLlnba⎞⎠
To find the current per unit length I′, we divide the total current I by the length L:
I′=IL=V⋅2πσlnba
Thus, the current per unit length flowing from one cylinder to the other is:
I′=2πσVlnba
Similar Questions
A long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionConsider a hollow cylinder of length L and inner radius a and outer radius b, as shown in figure. The material has resistivity ρ.
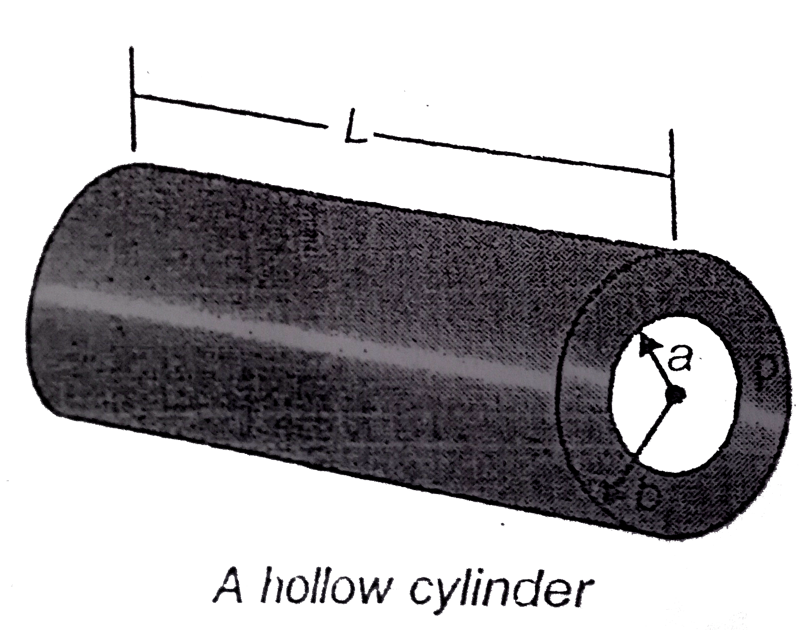
(a) Suppose a potential difference is applied between te ends of the cylinder and produces a current parallel to the axis. What is the resistance measure ?
(b) If instead the potential difference is applied between the inner outer surfaces so that current flows radially outward, what is the resistance measure ?View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
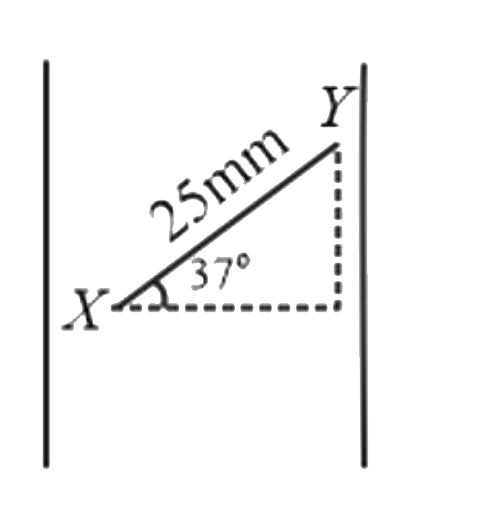 View Solution
View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
(a) K1+K2 (b) K1K2/(K1+K2)
(c )(K1+3K2)/4
(d) (3K1+K2)/4.View SolutionTwo conducting spheres of radii 3 cm and 1 m are separated by a distance of 10 cm in free space. If the spheres are charged to same potential of 10 V each, then the force of repulsion between them is
View SolutionA long cylinder of radius a carrying a uniform surface charge rotates about its axis with an angular velocity ω. Find the magnetic field energy per unit length of the cylinder if the linear charge density equals λ and μ=1.
View SolutionFind the force per unit area on the surface of a long hollow cylinder carrying uniform current I and radius of the cylinder is R.
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
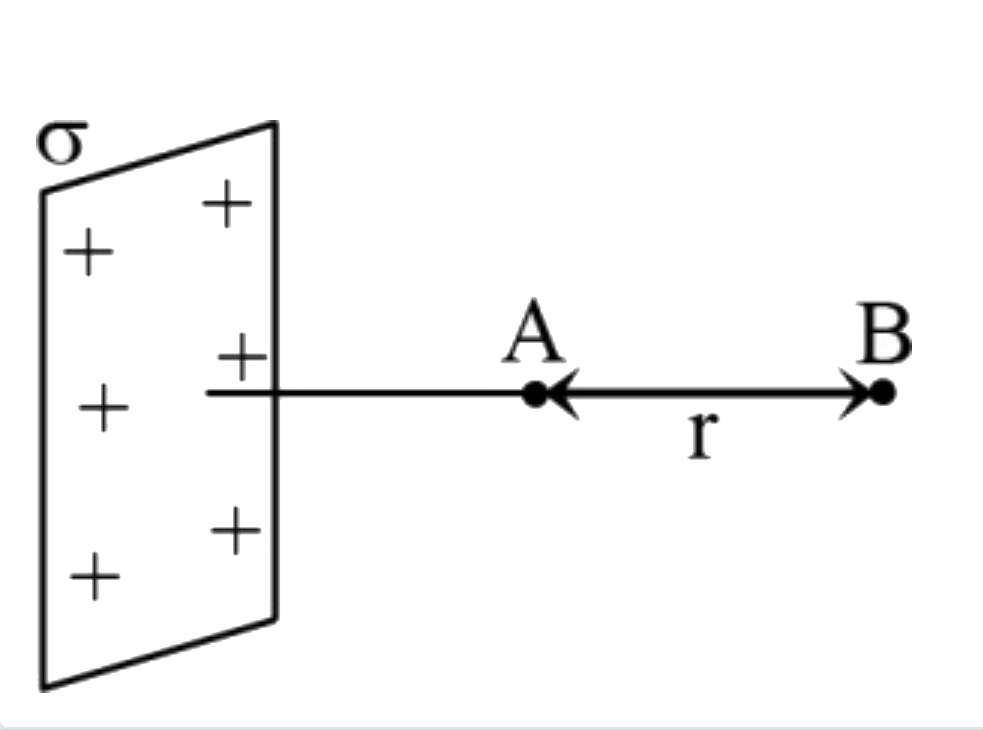 View Solution
View Solution

