The Young's double-slit experiment is done in a medium of refractive index 4/3. A light of 600 nm wavelength isfalling on the slits having 0.45 mm separation. The lower shift S2 is covered by a thin glass sheet of refractive index. 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in Figure
a. Find the location of central maximum (bright fringe with zero path difference) on the y-axis.
b. Find the light intensity of point O relative to the maximum fringe intensity.
c. Now , if 600 nm light is replaced by white light of range 400 - 700 nm, find the wavelengths of the light that from maxima exaclty at point O.
(All wavelength in the problem are for the given medium of refractive index 4/3 Ignoe dispersion.)
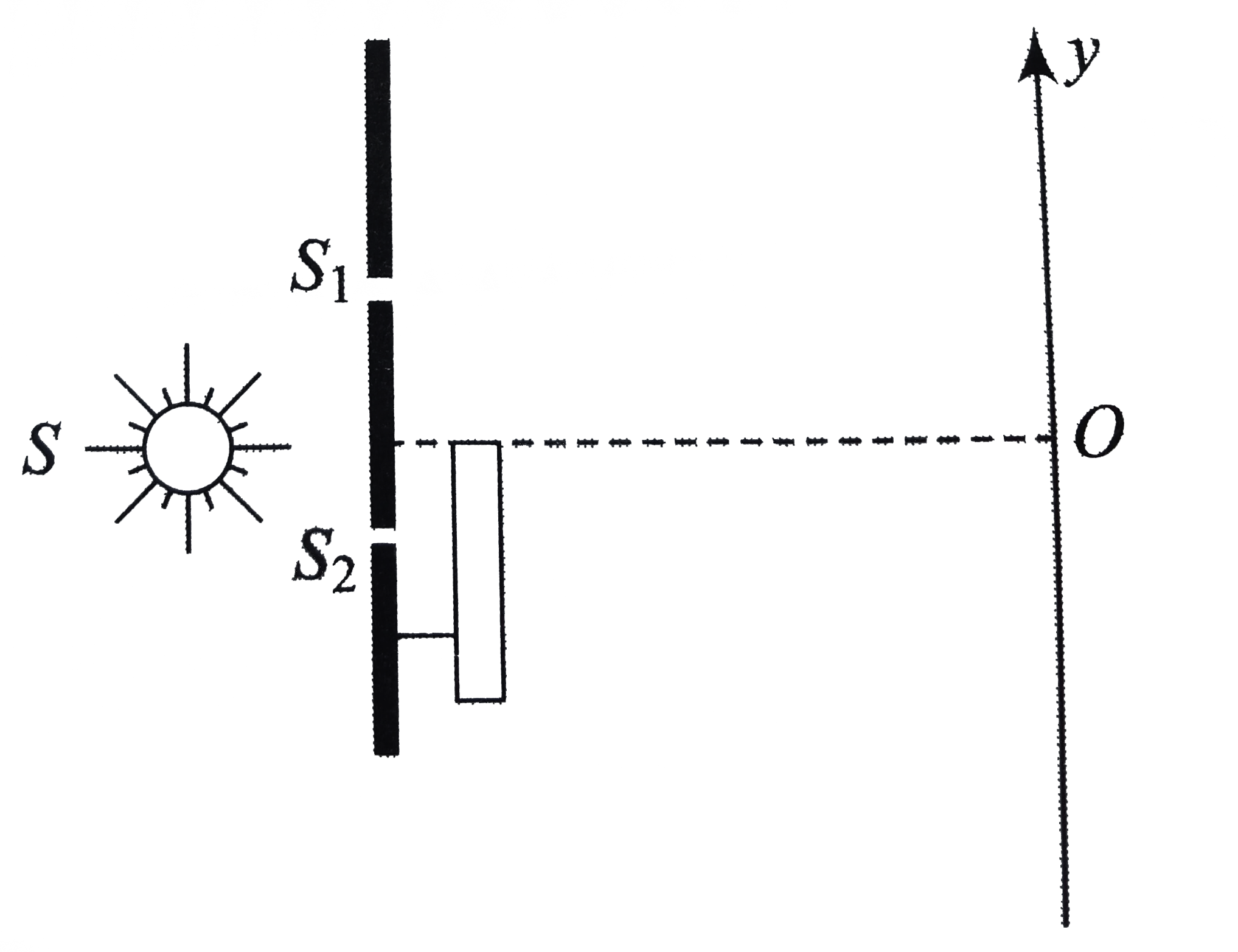
Given λnm=6×10−7m,d=0.45mm=0.45×10−3m,D=1.5. Thickness of glass sheet,
t=10.4μm=10.4×10−6m.
Refractive index of glass sheet, μg=1.5.
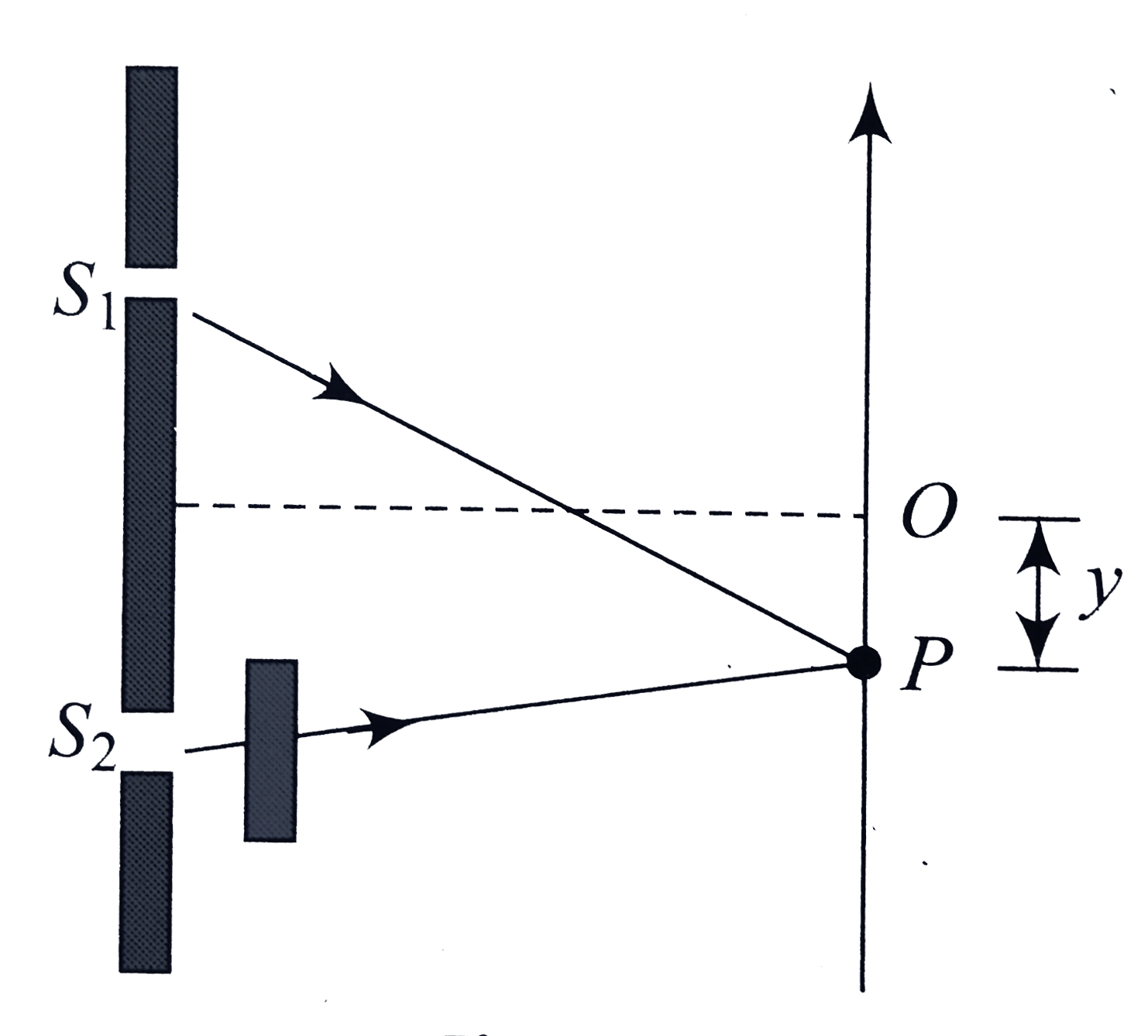
a. Let central maximum is obtained at a distance y below point O.Then,
Δx1=S1P−S2P=ydD
Path difference due to glass sheet,
Δx2=(μgμm−1)t
New path diffenence will be zero when
Δx1=Δx2
⇒ydd=(μgμm−1)t
⇒y=(μgμm−1)tDd
Subsituting the value, we have
y=(μgμm−1)tDd
or we can say y=4.33mm.
a. At O, Δx1=0 and Δx(2)=(μgμm−1)t
∴ Net path difference Δx=Δx2
Corresponding phase difference, Detlaϕ or simply
ϕ=2πλΔx.
Substituting the values, we have
ϕ=2π6×10−7(1.54/3−1)(10.4×10−6)=(133)π
Now,
I(ϕ)=Imaxcos2(ϕ2)
I=Imaxcos2(13π6)
=34Imax
At O, path difference is Δx=Δx2=(μgμm−1)t
For maximum intensity at O,
Δx=nλ (here n=1,2,3,...)
λ=Δx1,Δx2,Δx3,.... and so on
Δx=(1.54/3−1)(10.4×10−6m)
=(1.54/3−1)(10.4×10−3nm
=1300nm
Maximum intensity will be corresponding to
λ1300nm,13002nm,13003nm,13004nm,...
=1300nm,650nm,433.33nm,325nm,...
The wavelength in the range 400 to 700 nm are 650 nm and 433.33 nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
Find the light intensity at point O relative t maximum fringe intensity.
View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:

View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
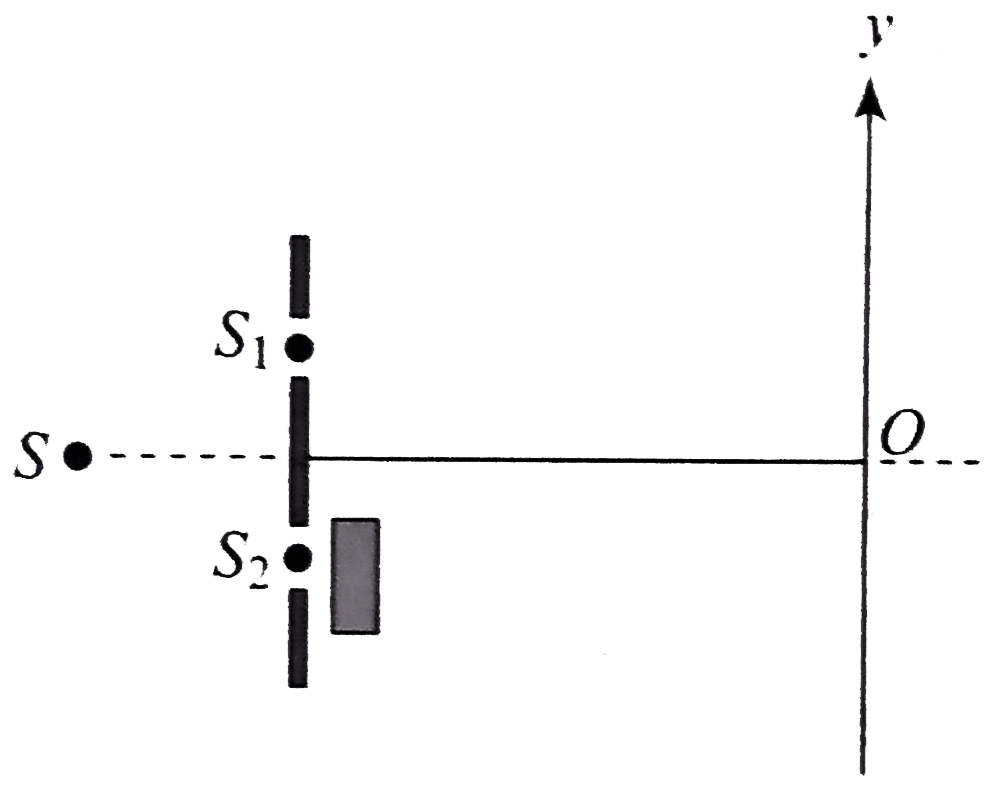
Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.
View SolutionTwo slits in YDSE are placed 1 mm from each other. Interference pattern is observed on a screen placed 1m from the plane of slits. What is the angular fringe width for a light of wavelength 400 nm
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
Find the distance of seventh bright fringe from third bright fringe lying on the same side of central bright fringe.
View SolutionA young's double slit apporatus is immersed in a liquid of refractive index 1.33.It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits.The wavelength in air is 6300Å
Calculate the fringe width.
View SolutionIn Young's experiment, light of wavelength 600 nm falls on the double slits separated by 0.1 mm. What is the highest order of maximum intensity in the interference pattern obtained on a screen kept 3 m from the slits? How does the highest order change if the distance of screen from the slits is changed?
View SolutionIn Yonung's double-slit experiment, two slits which are separated by 1.2 mm are illuminated with a monochromatic light of wavelength 6000Å The interference pattern is observed on a screen placed at a distance of 1 m from the slits. Find the number of bright fringes formed over 1 cm width on the screen.
View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
View Solution
