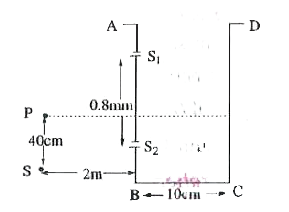
A vessel ABCD of 10cm width has two small slits S1 and S2 sealed with idebtical glass plates of equal thickness. The distance between the slits is 0.8mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S,40cm below P and 2m from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line OQ. Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

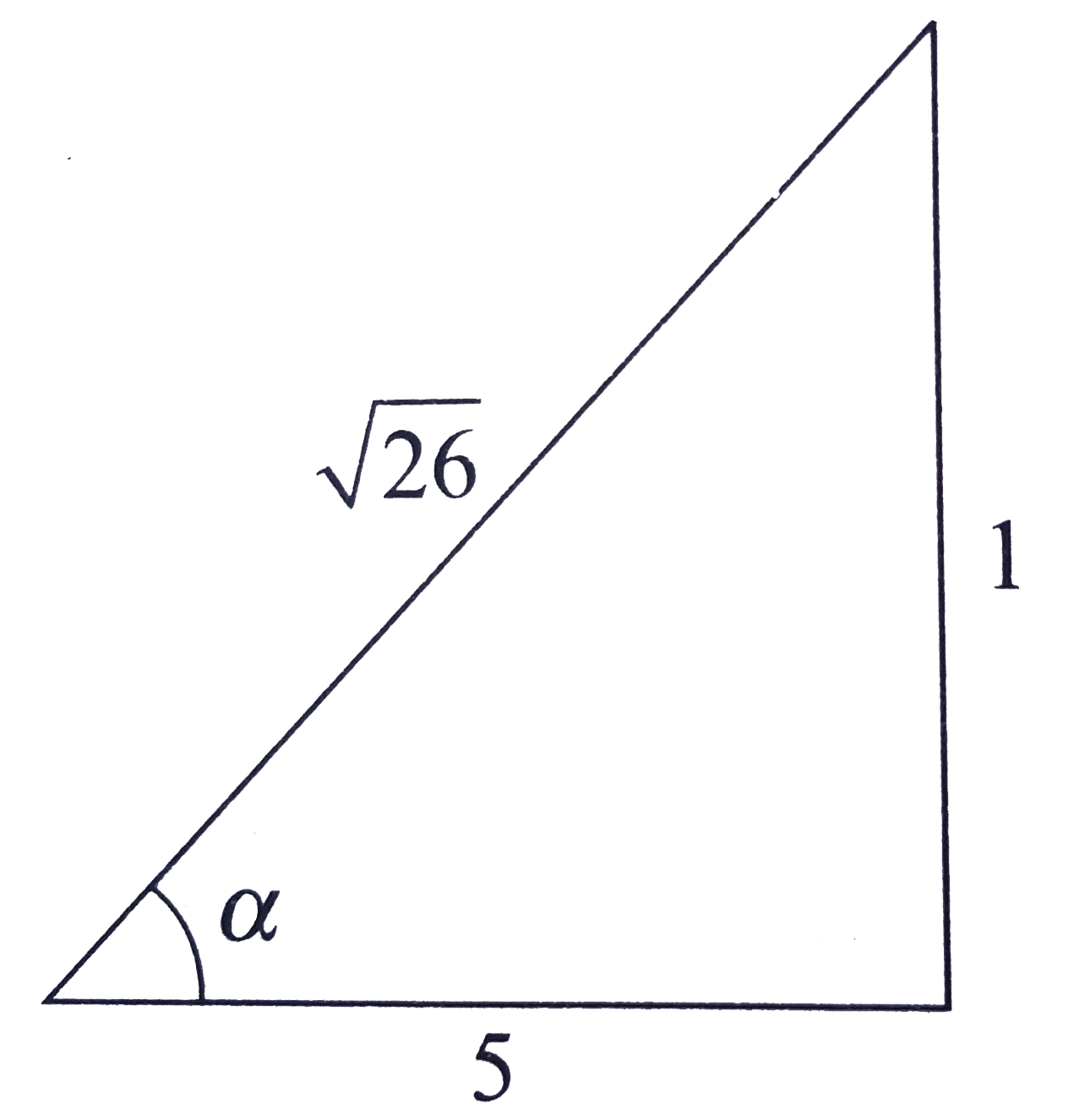
Given y1=40cm,D1=2m=200cm,D2=10cm.
tanα=y1D1=40200=15
α=tan−1(15)
sinα=1√26=15=tanα (see figure)
(BMSV04C02S01043_S01.png width=80%><br>Pathd⇔erencebetweenS S_(1)andS S_(2)is<br>Delta x_(1) = d sin alpha = (0.8 mm) ((1)/(5))<br>= 0.16 mm(i)<br>Now,≤tatp∮Ronthescreen,centralbright∈≥isobserved(i.e.,≠tpathd⇔erence=0).<br>Pathd⇔erec≠betweenS_(2) RandS_(1) Rwod––be<br> Delta x_(2) = S_(2) R - S_(1) R<br>= d sing theta<br>Centralbirght∈≥willbeobservedwhen≠tpathd⇔erence∈zer⊙<br>Delta x_(2) - Delta x_(1) = 0<br>Delta x_(2) = Delta x_(1)<br>d sin theta = 0.16<br>(0.8) sin theta = 0.16<br>sin theta = (0.16)/(0.8) = (1)/(5)<br>tan theta = (1)/(sqrt 24) ~~ sin theta = (1)/(5)<br>Hence,tan theta = (y_(2))/(D_(2)) = (1)/(5)<br>y_(2) = (D_(2))/(5) = (10)/(5) = 2 cm<br>Therefore,centralbright∈≥isobservedat2cmabovep∮OonsCD.<br>Delta xatRwillbezeroifDelta x_(1) = Delta x_(2)<br>d sin alpha = d sin theta<br>alpha = theta<br>tan alpha = tan theta<br>(y_(1))/(D_(1)) = (y_(2))/(D_(2))<br>y_(2) = (D_(2))/(D_(1)) y_(1) = ((10)/(200)) (40) cm<br>y_(2) = 2cm<br>Thecentralbright∈≥willbeobservedatp∮Q.Ifthepathd⇔erencecreatedbytheliqulabofthick≠sst = 10 cmor100mmisequal→Delta x,sotˆthe≠tpathd⇔erenceatQbecomeszero,then<br>(mu - 1) t = Delta x_(1)<br>implies (mu - 1) (100) = 0.16<br>implies mu-1 = 0.0016<br>implies mu = 1.0016
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.112videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.222videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
Two coherent sources of light of intensity ratio β produce interference pattern. Prove that in the interferencepattern
Imax−IminImax+(Imin)=2√β1+β
where Imax and Imin are maximum and mininum intensities in the resultant wave.02:02View SolutionIn Young's double slit experiment with wavelength 5890 Å, there are 60 fringe in the field of vision, How many fringes will be observed in the same field of vision id wavelength used is 5460 Å?
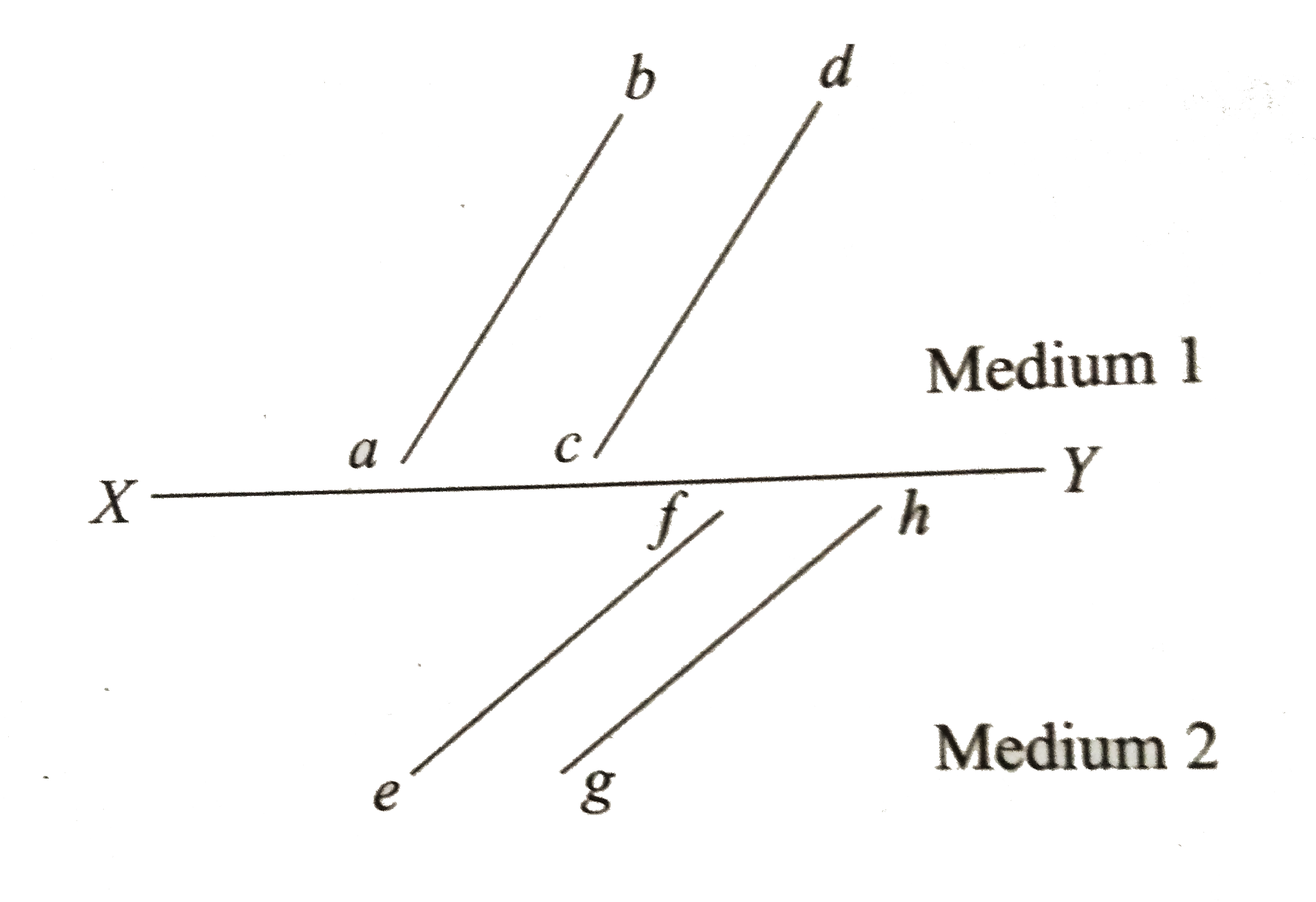
07:56View SolutionFig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.
Light travel as a04:06View SolutionThree distinct current wires intersect a finite rectangular plane ABCD. The current is left wire and the loop is l1 . The direction of current in left most wire and righy most loop is downards as shown in the figure. The current l2through middle wire is adjusted so that the path integal of the total magnetic field along the perimeter of the rectangle is zero , that is ,∮ABCDA→B.d→s=0 then the current I2 is
 02:01View Solution
02:01View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
07:20View SolutionIn a midified YDESE, sources S is kept in front of slit S_(1) . Find the phase difference at point O that is equidistant from slits S_(1) and S_(2) and point P that is in front of slit S_(1) in the following situations. ltgt Liquid is filled between the slit and source S.
View SolutionA vessel ABCD of 10 cm width has two small slits S_(1) and S_(2) sealed with idebtical glass plates of equal thickness. The distance between the slits is 0.8 mm . POQ is the line perpendicular to the plane AB and passing through O, the middle point of S_(1) and S_(2) . A monochromatic light source is kept at S, 40 cm below P and 2 m from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line OQ . Now, a liquid is poured into the vessel and filled up to OQ . The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.
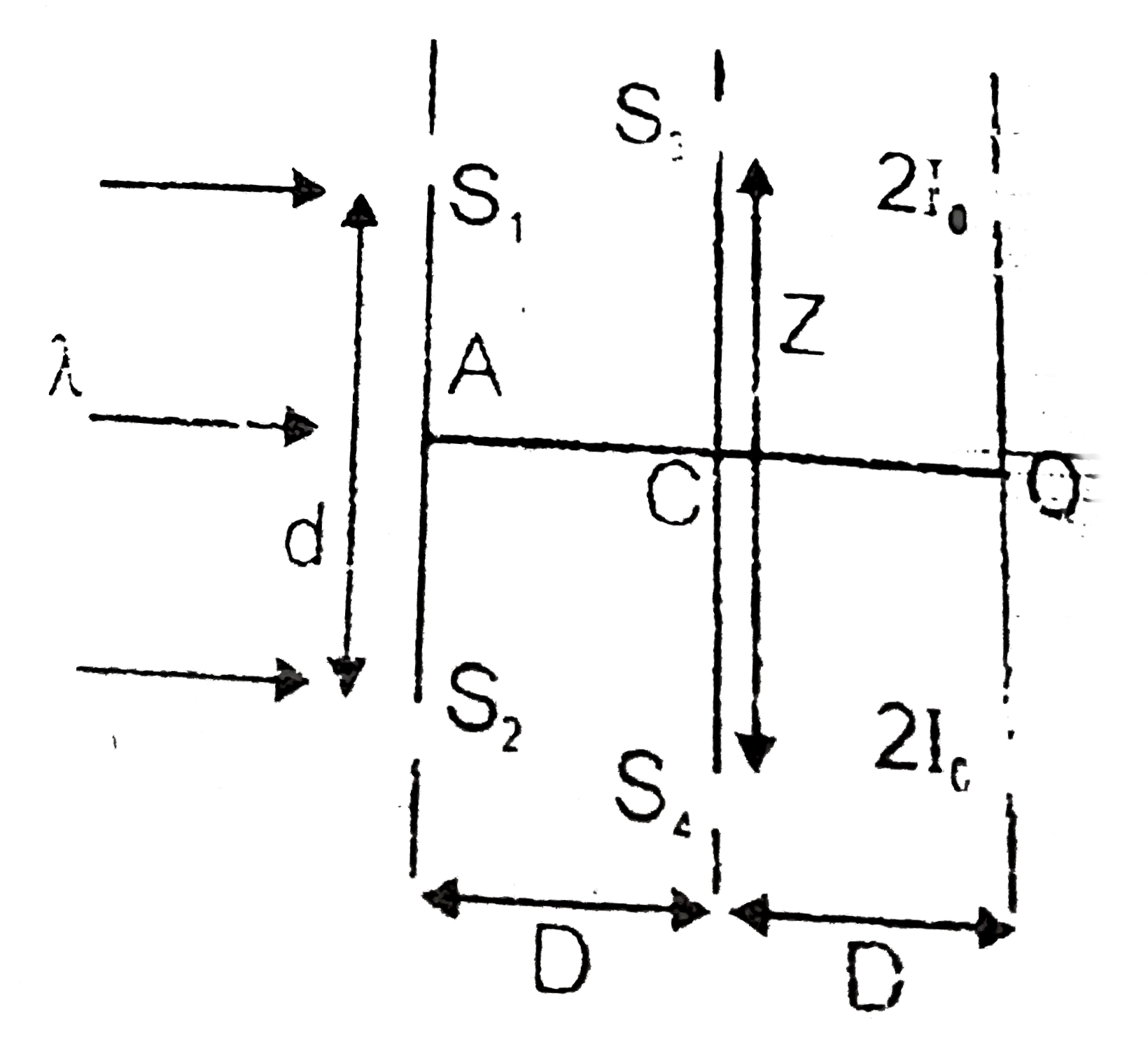
11:00View SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
 View Solution
View Solution10 cm चौड़ाई वाले एक पात्र ABCD में दो छोटी रेखाछिछ्र (द्वि-स्लिट) S1 और S2 चित्र में दर्शाया गया है बराबर मोटाई की समरूप कांच की प्लेटों के साथ बंद है। रेखाछिद्रों के बीच की दूरी 0.8 mm है। POQ, तल AB के लंबवत और O जो S1 और S2 का मध्य बिंदु है से गुजरने वाली रेखा है।
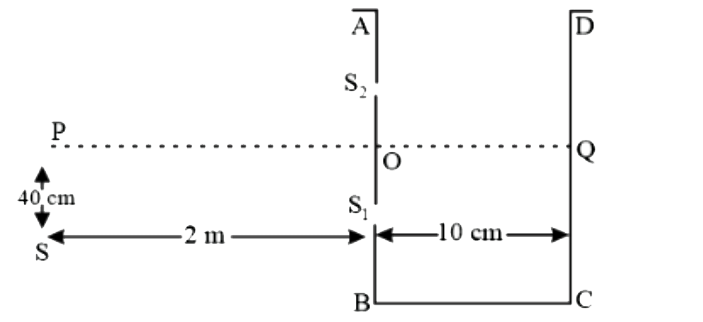
एक एकवर्णी प्रकाश स्रोत, जो S पर रखा है 40 cm, P के नीचे और पात्र से 2m पर, रेखाछिद्रों को प्रकाशित करने के लिए रखा जाता है जैसा कि आकृति में दिखाया गया है। पात्र में एक द्रव को OQ तक भरने के बाद यह पाया गया कि केंद्रीय दीप्त फ्रिंज अब Q पर स्थित है। उस द्रव का अपवर्तनांक है05:14View SolutionTwo coherent point sources S_(1) and S_(2) vibrating in phase emit light of wavelength lambda .The separation between the sources is 2 lambda .The smallest distance from S_(2) on a line passing through S_(2) and perpendicular to S_(1)S_(2) where a minimum intensity occurs is :
View SolutionA vessel ABCD of 10 cm width has two small slits s1 and S2 sealed, with identical glass plates of equal thickness. The distance between the slits is 0.8. mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept al S. 40 cm below P and 2m from the vessel, to illuminate the slits as shown in the figure below. 40cm Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled up to-OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid
View SolutionA vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1. A monochromatic light source is kept at S, 40 cm below P and 2m from the vessel to illuminate the slits as shown in fig. The position of the central bright fringe on the other wall CD w.r.t. the line OQ.
 07:20View Solution
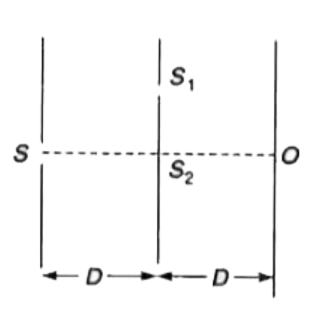
07:20View Solutionदो आदर्श स्लिटो S1 व S2 को एक λ तरंगदैर्ध्य वाले आदर्श स्लिट स्त्रोत S द्वारा प्रकाशित किया जाता है। स्लिट S चित्रानुसार S2 के ठीक पीछे स्थित है। स्त्रोत स्लिट S एवं (S1,S2) स्लिटो के तलो के बीच की दूरी D है। एक पर्दा स्लिटो के तल से D दूरी पर स्थित है। स्लिटो (S1,S2) के बीच की दूरी (d) का न्यूनतम मान क्या होना चाहिए ताकि बिंदु O पर अदीप्त फ्रिन्ज प्राप्त हो?
 01:18View Solution
01:18View SolutionIn an interference experiment , two parallel verticals slits S1 and S2 are used. A thin glass plate is introduced in the path of light from S1. Then
05:22View SolutionA vessel ABCD of 10 cm width has two small slits S_(1) and S_(2) sealed with identical glass paltes of equal thickness . The distance between the slits is 0.8 mm . POQ is the line perpendicular to the plane AB and passing through O , the middle point of S_(1) and S_(2) .A monochromatic light source is kept at S , 40 cm below P and 2m from the vessel to illuminate the slits as shown in fig. The position of the cnetral bright fringe on the other wall CD w.r.t the line OQ.
03:57View Solution

