To produce a minimum reflection of wavelength near the middle of visible spectrum (550 nm), how thick should a coating of MgF2(μ=1.38) be vaccum-coated on a glass surface?
10−7 m
10−10 m
10−9 m
10−8 m
The correct Answer is:a
To solve the problem of determining the thickness of the MgF₂ coating needed to produce minimum reflection for a wavelength of 550 nm, we can follow these steps:
Step 1: Understand the condition for minimum reflection
For a thin film to produce minimum reflection, the path difference between the light waves reflected from the top and bottom surfaces of the film must be an odd multiple of half the wavelength. This condition can be expressed as:
Δx=(2n−1)λ2
where n is an integer (1, 2, 3, ...) and λ is the wavelength of light in vacuum.
Step 2: Calculate the total path difference
The total path difference for light reflecting off the two surfaces of the film is given by:
Δx=2μt
where μ is the refractive index of the film (MgF₂ in this case), and t is the thickness of the film.
Step 3: Set the two expressions for path difference equal
To find the thickness t that results in minimum reflection, we set the two expressions for path difference equal:
2μt=(2n−1)λ2
Step 4: Solve for thickness t
Rearranging the equation to solve for t:
t=(2n−1)λ4μ
Step 5: Substitute known values
We are given:
- Wavelength λ=550nm=550×10−9m
- Refractive index μ=1.38
For minimum thickness, we can take n=1:
t=(2⋅1−1)⋅550×10−94⋅1.38
t=1⋅550×10−94⋅1.38
t=550×10−95.52
t≈99.64×10−9m=0.09964μm
Step 6: Final answer
Thus, the thickness of the MgF₂ coating should be approximately:
t≈100nm
For a thin film to produce minimum reflection, the path difference between the light waves reflected from the top and bottom surfaces of the film must be an odd multiple of half the wavelength. This condition can be expressed as:
Δx=(2n−1)λ2
where n is an integer (1, 2, 3, ...) and λ is the wavelength of light in vacuum.
The total path difference for light reflecting off the two surfaces of the film is given by:
Δx=2μt
where μ is the refractive index of the film (MgF₂ in this case), and t is the thickness of the film.
To find the thickness t that results in minimum reflection, we set the two expressions for path difference equal:
2μt=(2n−1)λ2
Rearranging the equation to solve for t:
t=(2n−1)λ4μ
We are given:
- Wavelength λ=550nm=550×10−9m
- Refractive index μ=1.38
t=(2⋅1−1)⋅550×10−94⋅1.38
t=1⋅550×10−94⋅1.38
t=550×10−95.52
t≈99.64×10−9m=0.09964μm
Thus, the thickness of the MgF₂ coating should be approximately:
t≈100nm
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
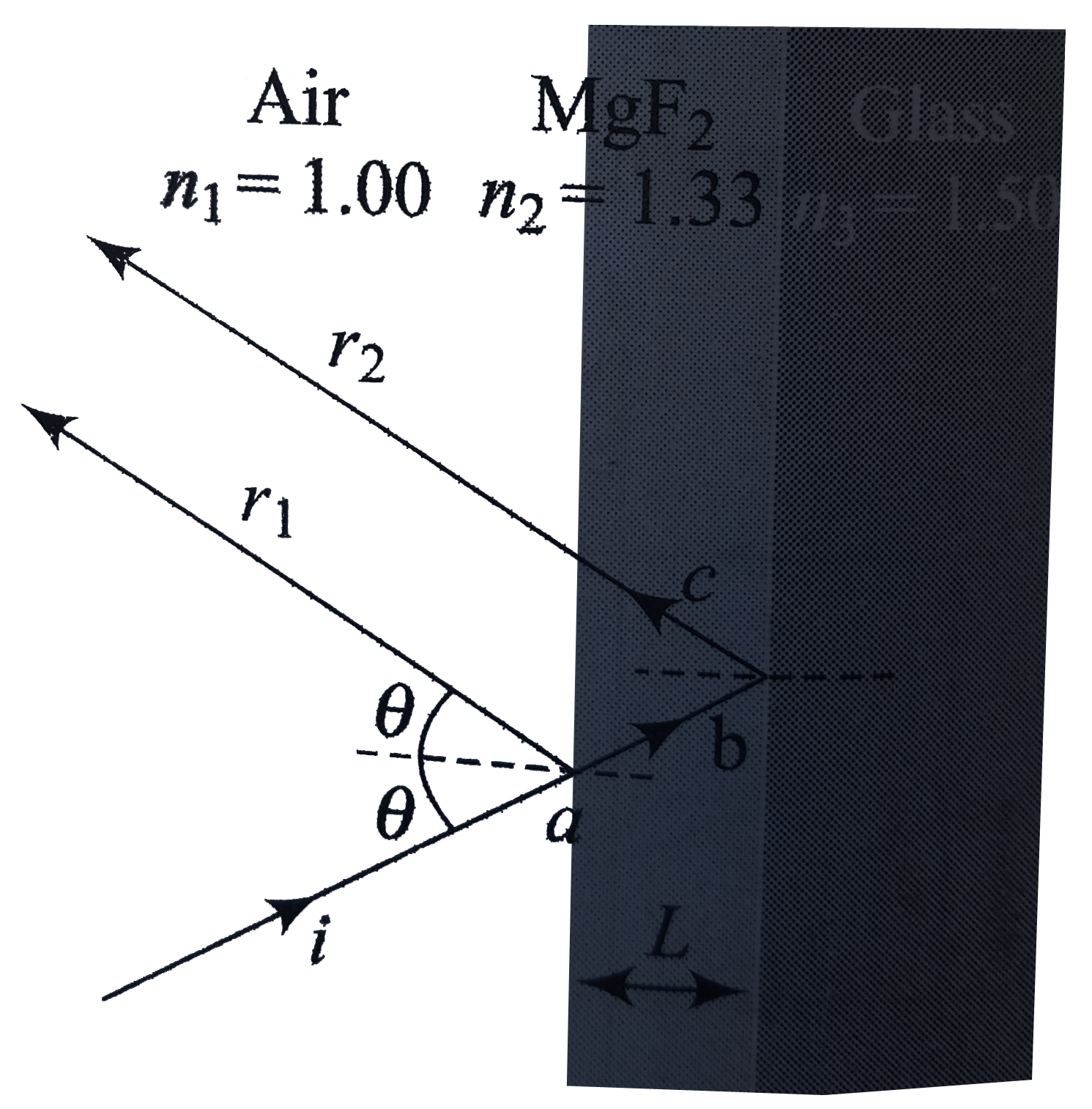
View SolutionIn solar cells, a silicon solar cell (μ=3.5) is coated with a thin film
of silicon monoxide SiO(μ=1.45) to minimize reflective losses from the surface.
Determine the minimum thickness of SiO that produces the least reflection at a
wavelength of 550nm, near the centre of the visible spectrum. Assume
approximately normal incidence .
View SolutionIn solar cells, a silicon solar cell (μ=3.5) is coated with a thin film
of silicon monoxide SiO(μ=1.45) to minimize reflective losses from the surface.
Determine the minimum thickness of SiO that produces the least reflection at a
wavelength of 550nm, near the centre of the visible spectrum. Assume
approximately normal incidence .
View SolutionA possible means for making an airplane invisible to radar is to coat the plane with an anti reflective polymer. If radar waves have a wavelength of 3.00 cm and the index of refraction of the polymer is μ=1.5. How thick is the oil film? Refractive index of the material of airplane wings is greater than the refractive index of polymer.
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionA glass plate (n=1.53) that is 0.485 μ m thick and surrounded by air is illuminated by a beam of white light normal to the plate.
(a) What wavelengths (in air) within the limits of the visible spectrum (λ=400to700nm) are intensified in the reflected beam ?
(b) What wavelengths within the visible spectrum are intensified in the transmitted light?
View SolutionA soap film of thickness 0.0011 mm appears dark when seen by the reflected light of wavelength 580 nm.. What is the index of refraction of the soap solution, if it is known to be between 1-2 and 1.5 ?
View SolutionOn face of a glass (μ=1.50) lens is coated with a thin film of magnesium fluoride MgF2(μ=1.38) to reduce reflection from the lens surface. Assuming the incident light to be perpendicular to the lens surface. The least coating thickness that eliminates the reflection at the centre of the visible spectrum (λ=550nm) is about
View SolutionA thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating (n1) is less than that of the glass (n2).

5. magnesium fluoride (MgF2) is generally use as anti-reflection coating. If refractive index of MgF2 is 1.25, then minimum thickness of film required is (Take λ=500nm)
View SolutionTo ensure almost 100% transmittivity, photographic lenses are often coated with a thin layer of dielectric material, like MgF2(μ=1.38) . The minimum thickness of the film to be used so that at the centre of visible spectrum (λ=5500Å) there is maximum transmission.
View Solution