In solar cells, a silicon solar cell (μ=3.5) is coated with a thin film
of silicon monoxide SiO(μ=1.45) to minimize reflective losses from the surface.
Determine the minimum thickness of SiO that produces the least reflection at a
wavelength of 550nm, near the centre of the visible spectrum. Assume
approximately normal incidence .
To determine the minimum thickness of silicon monoxide (SiO) that minimizes reflective losses at a wavelength of 550 nm, we can follow these steps:
1. Identify Given Values:
- Wavelength of light, λ=550nm=550×10−9m
- Refractive index of silicon (solar cell), μ1=3.5
- Refractive index of silicon monoxide (SiO), μ2=1.45
2. Understand the Condition for Minimum Reflection:
- For a thin film to minimize reflection, the condition is that the optical path difference between the light reflected from the top surface and the light reflected from the bottom surface of the film must be an odd multiple of half the wavelength. This is mathematically expressed as:
2μ2T=λ2
- Here, T is the thickness of the film.
3. Rearranging the Formula:
- To find the thickness T, we can rearrange the equation:
T=λ4μ2
4. Substituting the Values:
- Now substituting the values into the equation:
T=550×10−9m4×1.45
5. Calculating the Thickness:
- First, calculate 4×1.45=5.8.
- Now, substitute this value into the equation:
T=550×10−95.8
- Performing the division:
T≈9.48×10−8m=94.8nm
6. Final Result:
- The minimum thickness of silicon monoxide (SiO) that produces the least reflection at a wavelength of 550 nm is approximately:
T≈94.8nm
- Wavelength of light, λ=550nm=550×10−9m
- Refractive index of silicon (solar cell), μ1=3.5
- Refractive index of silicon monoxide (SiO), μ2=1.45
- For a thin film to minimize reflection, the condition is that the optical path difference between the light reflected from the top surface and the light reflected from the bottom surface of the film must be an odd multiple of half the wavelength. This is mathematically expressed as:
2μ2T=λ2
- Here, T is the thickness of the film.
- To find the thickness T, we can rearrange the equation:
T=λ4μ2
- Now substituting the values into the equation:
T=550×10−9m4×1.45
- First, calculate 4×1.45=5.8.
- Now, substitute this value into the equation:
T=550×10−95.8
- Performing the division:
T≈9.48×10−8m=94.8nm
- The minimum thickness of silicon monoxide (SiO) that produces the least reflection at a wavelength of 550 nm is approximately:
T≈94.8nm
Topper's Solved these Questions
Similar Questions
On face of a glass (μ=1.50) lens is coated with a thin film of magnesium fluoride MgF2(μ=1.38) to reduce reflection from the lens surface. Assuming the incident light to be perpendicular to the lens surface. The least coating thickness that eliminates the reflection at the centre of the visible spectrum (λ=550nm) is about
View SolutionA thin film of thickness t and index of refractive 1.33 coats a glass with index of refraction 1.50.What is the least thickness t that will strong reflect light with wavelength 600nm incident normally?
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
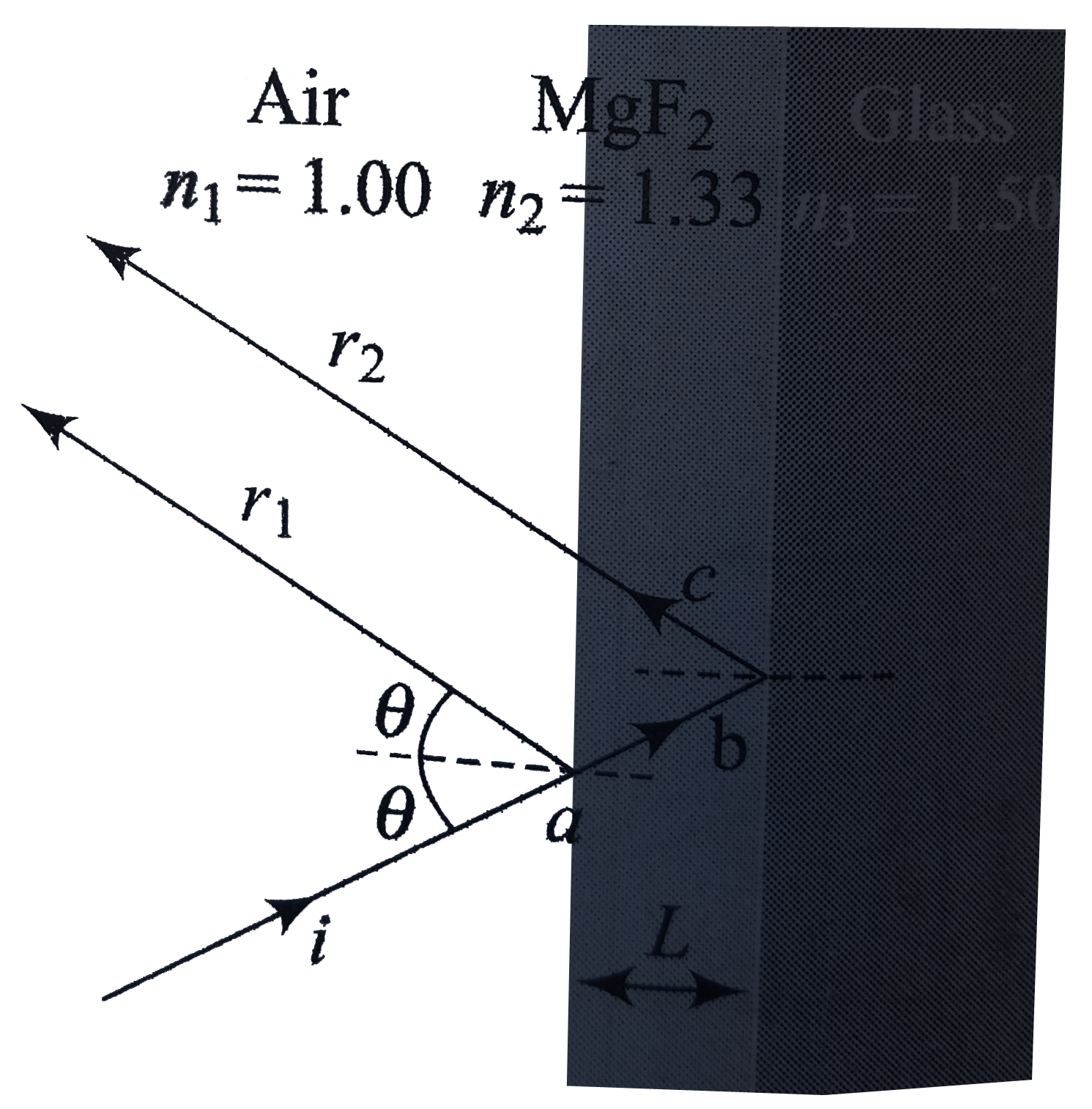 View Solution
View SolutionA thin film of refractive index 1.5 and thickness 4×10−5 cm is illuminated by light normal to the surface. What wavelength within the visible spectrum will be intensified in the reflected beam?
View SolutionHigh-quality camera lenses are often coated to prevent reflection. A lens has an optical index of refraction of 1.72 and a coating with an optical index os refraction 1.31. For near normal incidence, the minimum thickness of the coating to prevent reflection for wavelength of 5.3×10−7m is
View SolutionTo produce a minimum reflection of wavelength near the middle of visible spectrum (550 nm), how thick should a coating of MgF2(μ=1.38) be vaccum-coated on a glass surface?
View SolutionA thin film of soap solution (μs=1.5). When visible light is incident almost normal to the plate, two wavelength 420 nm and 630 nm are strongly reflected. What is the minimum thickness (in nm) of the soap film?
View SolutionBlue light of wavelength 480 nm is most strongly reflected off a thin film of oil on a glass slab when viewed near normal incidence. Assuming that the index of refraction of the oil is 1.2 and that of the glass is 1.6, what is the minimum thickness of the oil film (other then zero)?
View SolutionA thick glass slab (μ=1.5) is to be viewed in reflected white light. It is proposed to coat the slab with a thin layer of a material having refractive index 1.3 so that the wavelength 6000 Å os suppressed. Find the minimum thickness of the coating required.
View SolutionA glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
View Solution

