Two identical coherent sources of wavelength λ are placed at (100λ,0) and (−50λ,0) along x-axis. The number of maxima and minima detected are ,respectively [include origin and (5λ,0)]
51 and 50
101 and 100
49 and 50
50 and 49
The correct Answer is:b
To solve the problem, we need to determine the number of maxima and minima produced by the two coherent sources located at (100λ, 0) and (-50λ, 0) along the x-axis.
1. Identify the Positions of the Sources:
The two coherent sources are located at:
- Source S1 at (100λ, 0)
- Source S2 at (-50λ, 0)
2. Calculate the Distance Between the Sources (d):
The distance d between the two sources can be calculated as:
d=100λ−(−50λ)=100λ+50λ=150λ
3. Determine the Path Difference for Maxima:
The path difference Δx for maxima is given by:
Δx=d=150λ
4. Calculate the Order of Maxima (n):
The order of maxima n can be calculated using the formula:
n=dλ=150λλ=150
5. Total Number of Maxima:
The total number of maxima includes the central maximum and the maxima on both sides:
- There is 1 central maximum.
- There are 150 maxima on one side and 150 on the other side.
Therefore, the total number of maxima is:
Total Maxima=1+150+150=301
6. Total Number of Minima:
The total number of minima can be calculated similarly:
- Between each pair of maxima, there is one minima.
- There are 150 maxima on one side and 150 on the other side, leading to 150 minima on each side.
Therefore, the total number of minima is:
Total Minima=150+150=300
Final Answer:
The total number of maxima is 301, and the total number of minima is 300.
The two coherent sources are located at:
- Source S1 at (100λ, 0)
- Source S2 at (-50λ, 0)
The distance d between the two sources can be calculated as:
d=100λ−(−50λ)=100λ+50λ=150λ
The path difference Δx for maxima is given by:
Δx=d=150λ
The order of maxima n can be calculated using the formula:
n=dλ=150λλ=150
The total number of maxima includes the central maximum and the maxima on both sides:
- There is 1 central maximum.
- There are 150 maxima on one side and 150 on the other side.
Therefore, the total number of maxima is:
Total Maxima=1+150+150=301
The total number of minima can be calculated similarly:
- Between each pair of maxima, there is one minima.
- There are 150 maxima on one side and 150 on the other side, leading to 150 minima on each side.
Therefore, the total number of minima is:
Total Minima=150+150=300
The total number of maxima is 301, and the total number of minima is 300.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
Two coherent sources emit light of wavelength λ. Separation between them, d=4λ.
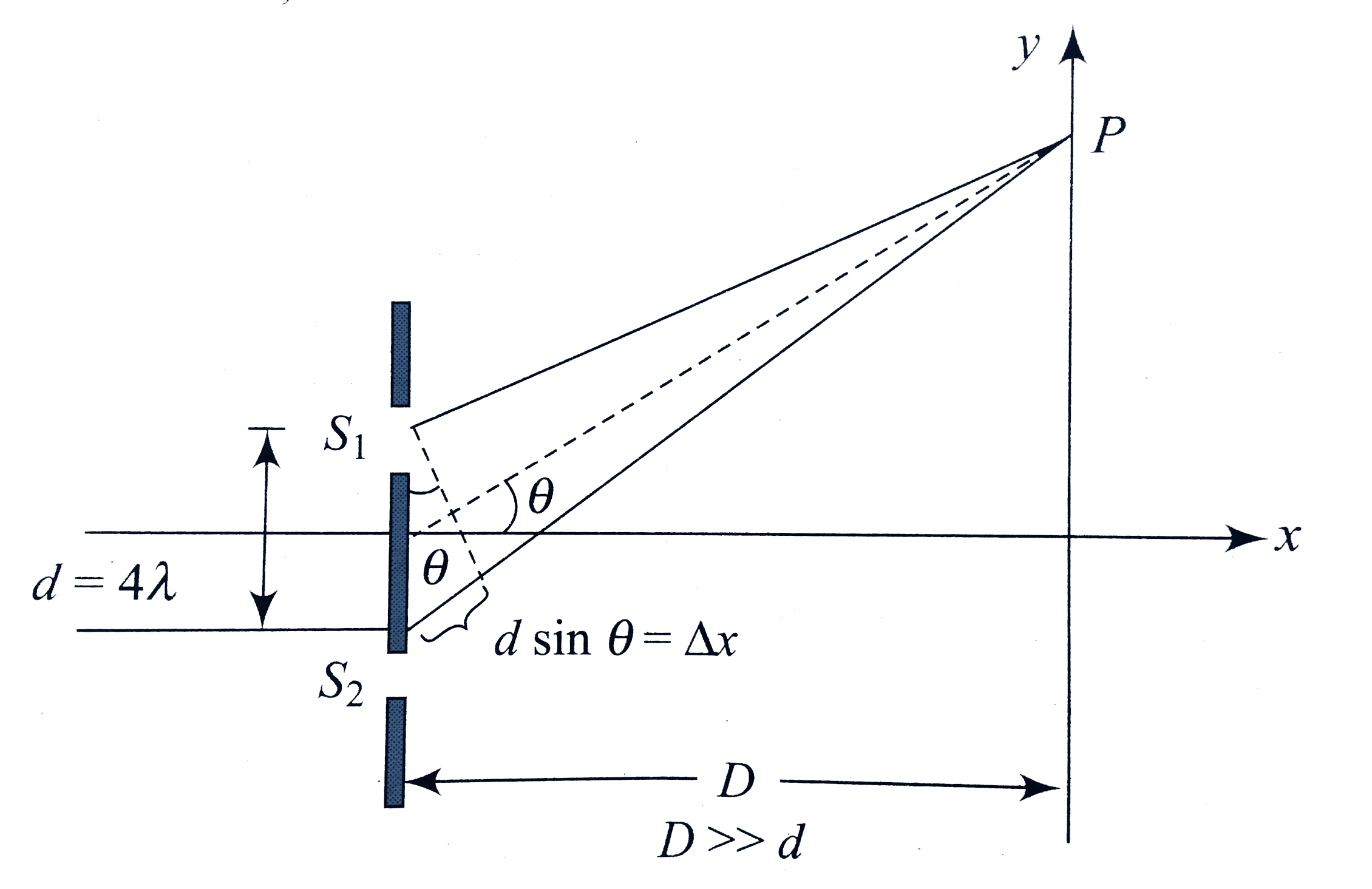
If a detector moves along the y-axis, what is the maximum number of minima observed?
View SolutionTwo coherent light sources, each of wavelength λ, are separated by a distance 3λ, The maximum number of minima formed on line AB, which funs from −∞ to +∞, is

View SolutionFour monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
View SolutionTwo identical metal plates show photoelectric effect by a light of wavelength λA falling on plate A and λB on plate B(λA=2λB). The maximum kinetic energy is
View SolutionAn interference is observed due to two coherent sources S1 placed at origin and S2 placed at (0,3λ,0). Here, lambda is the wavelength of the sources. A detector D is moved along the positive x-axis. Find x-coordinates on the x-axis (excluding x=0andx=∞) where maximum intensity is observed.
View SolutionTwo coherent light sources A and B are at a distance 3λ from each other (λ=wavelength)The distances from A on the X-axis at which the interference is constructive are
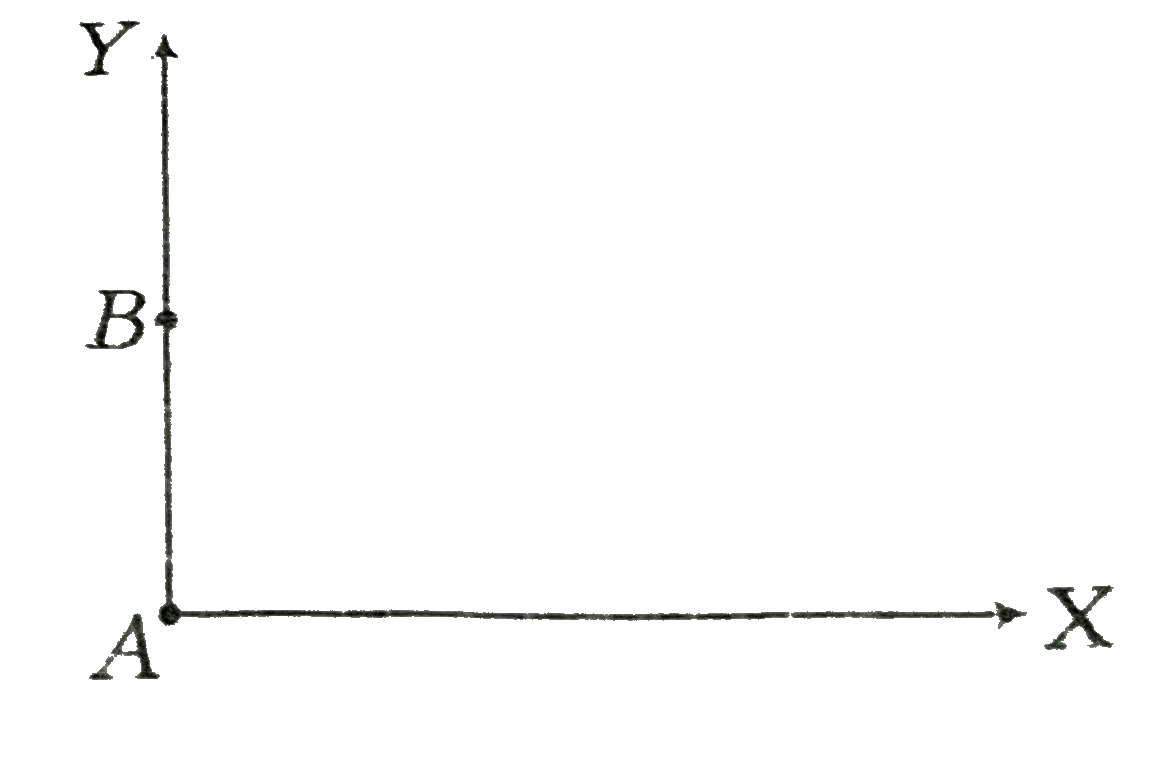
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=5λ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
View SolutionIf λ1 and λ2 are the wavelength of characteristic X - rays and gamma rays respectively , then the relation between them is
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionTwo identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
View Solution
