A certain region of a soap bubble reflects red light of vacuum wavelength λ=650nm. What is the minimum thickness that this region of the soap bubble could be have? Take the index of reflection of the soap film to be 1.41.
1.2×10−7m
650×10−9m
120×107m
650×105m
The correct Answer is:a
To find the minimum thickness of the soap bubble that reflects red light of wavelength λ=650nm (or 650×10−9m), we can use the concept of interference in thin films. Here's the step-by-step solution:
Step 1: Understanding the Interference Condition
When light reflects off a thin film (like a soap bubble), there are two reflections to consider:
1. The first reflection occurs at the top surface (air-soap interface).
2. The second reflection occurs at the bottom surface (soap-air interface).
For constructive interference, the optical path difference must be an integer multiple of the wavelength. However, since there is a phase change of λ/2 upon reflection at the denser medium (soap), we need to account for this in our calculations.
Step 2: Setting Up the Optical Path Difference
The optical path difference (OPD) for the light reflecting off the two surfaces is given by:
OPD=2μt−λ2
where:
- μ is the refractive index of the soap film (given as 1.41),
- t is the thickness of the soap film,
- λ is the wavelength of light in vacuum.
For constructive interference, we set the OPD equal to mλ (where m is an integer):
2μt−λ2=mλ
Step 3: Rearranging the Equation
Rearranging the equation gives:
2μt=mλ+λ2
2μt=(m+12)λ
t=(m+12)λ2μ
Step 4: Finding Minimum Thickness
To find the minimum thickness, we take m=0:
tmin=(0+12)λ2μ=λ4μ
Step 5: Substituting Values
Now, substituting the values of λ and μ:
tmin=650×10−9m4×1.41
Calculating this gives:
tmin=650×10−95.64≈115.4×10−9m≈1.154×10−7m
Final Answer
Thus, the minimum thickness tmin of the soap bubble is approximately:
tmin≈1.15×10−7m or 115.4nm
When light reflects off a thin film (like a soap bubble), there are two reflections to consider:
1. The first reflection occurs at the top surface (air-soap interface).
2. The second reflection occurs at the bottom surface (soap-air interface).
The optical path difference (OPD) for the light reflecting off the two surfaces is given by:
OPD=2μt−λ2
where:
- μ is the refractive index of the soap film (given as 1.41),
- t is the thickness of the soap film,
- λ is the wavelength of light in vacuum.
2μt−λ2=mλ
Rearranging the equation gives:
2μt=mλ+λ2
2μt=(m+12)λ
t=(m+12)λ2μ
To find the minimum thickness, we take m=0:
tmin=(0+12)λ2μ=λ4μ
Now, substituting the values of λ and μ:
tmin=650×10−9m4×1.41
Calculating this gives:
tmin=650×10−95.64≈115.4×10−9m≈1.154×10−7m
Thus, the minimum thickness tmin of the soap bubble is approximately:
tmin≈1.15×10−7m or 115.4nm
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
A material having an index of refraction of 1.30 is used as an antireflective coating on a piece of glass (n = 1.50). What should be the minimum thickness of this film in order to minimize reflection of 500 nm light?
View SolutionFind the minimum thickness of a film which will strongly reflect the light of wavelength 589 nm. The refractive index of the material of the film is 1.25.
View SolutionA soap film of thickness 0.0011 mm appears dark when seen by the reflected light of wavelength 580 nm.. What is the index of refraction of the soap solution, if it is known to be between 1-2 and 1.5 ?
View SolutionA film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View SolutionA thin uniform film of refractive index 1.75 is placed on a sheet of glass of refractive index 1.5. At room temperature (20∘C) this film is just thick enoungh for light with wavelength 600 nm reflected off the top of the film to be canceled by light reflected from the top the glass. After the glass is placed in on oven and slowly heated to 170∘C, the film conceals reflected light with wavelength 606 nm. The coefficient of linear expansion of the film is (ignore any changes in the refractive index of the film due to the temperature change)
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionA thin film of a specific meterial can be used to decrease the intensity of reflected light. There is destrucive inteference of wave reflected from upper and lower surface of the film. These films are called non-reflecting or anti-reflecting coatings. The process of coating the lens or surface with non-reflecting film is called blooming as shown in figure The refracting index of coating (n1) is less than that of the glass (n2).

4. If a light of wavelength λ is incident normally and the thickness of film is t, then optical path difference between waves reflected from upper and lower surface of the film isView SolutionDetermine what happens to the double slits interference pattern if one of the slits is covered with a thin, transparent film whose thickness is λ2(μ−1), where λ is the wavelength of the incident light and mu is the index of refraction of the film.
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
The average human eye sees colors with wavelength between 430 nm to 680 nm. For what visible wavelength (s) will a 350 nm thick (n=1.35) soap film produce maximum destructive interference?View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride (MgF2)to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of MgF2 is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm (λ=550nm)? Assume that the light is approxmately perpendicular to the lens surface.
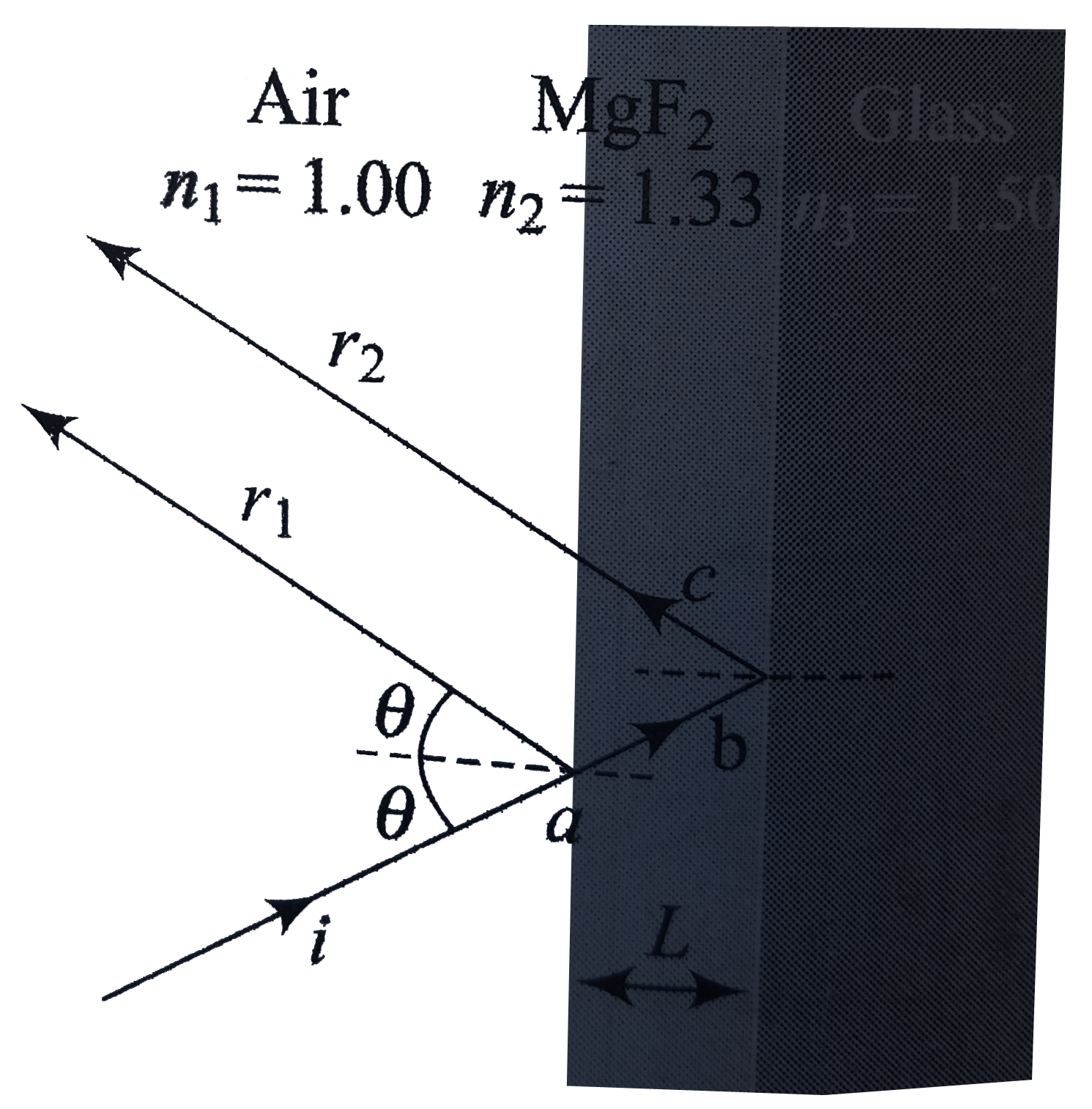 View Solution
View Solution



